A novel algorithm for the decomposition of non-stationary multidimensional and multivariate signals

The decomposition of a signal is a fundamental tool in many fields of research, including signal processing, geophysics, astrophysics, engineering, medicine, and many more. By breaking down complex signals into simpler oscillatory components we can enhance the understanding and processing of the data, unveiling hidden information contained in them. Traditional methods, such as Fourier analysis and wavelet transforms, which are effective in handling mono-dimensional stationary signals struggle with non-stationary data sets and they require, this is the case of the wavelet, the selection of predefined basis functions. In contrast, the Empirical Mode Decomposition (EMD) method and its variants, such as Iterative Filtering (IF), have emerged as effective nonlinear approaches, adapting to signals without any need for a priori assumptions. To accelerate these methods, the Fast Iterative Filtering (FIF) algorithm was developed, and further extensions, such as Multivariate FIF (MvFIF) and Multidimensional FIF (FIF2), have been proposed to handle higher-dimensional data. In this work, we introduce the Multidimensional and Multivariate Fast Iterative Filtering (MdMvFIF) technique, an innovative method that extends FIF to handle data that vary simultaneously in space and time. This new algorithm is capable of extracting Intrinsic Mode Functions (IMFs) from complex signals that vary in both space and time, overcoming limitations found in prior methods. The potentiality of the proposed method is demonstrated through applications to artificial and real-life signals, highlighting its versatility and effectiveness in decomposing multidimensional and multivariate nonstationary signals. The MdMvFIF method offers a powerful tool for advanced signal analysis across many scientific and engineering disciplines.

RRCNN$^{+}$: An Enhanced Residual Recursive Convolutional Neural Network for Non-stationary Signal Decomposition

Time-frequency analysis is an important and challenging task in many applications. Fourier and wavelet analysis are two classic methods that have achieved remarkable success in many fields. They also exhibit limitations when applied to nonlinear and non-stationary signals. To address this challenge, a series of nonlinear and adaptive methods, pioneered by the empirical mode decomposition method have been proposed. Their aim is to decompose a non-stationary signal into quasi-stationary components which reveal better features in the time-frequency analysis. Recently, inspired by deep learning, we proposed a novel method called residual recursive convolutional neural network (RRCNN). Not only RRCNN can achieve more stable decomposition than existing methods while batch processing large-scale signals with low computational cost, but also deep learning provides a unique perspective for non-stationary signal decomposition. In this study, we aim to further improve RRCNN with the help of several nimble techniques from deep learning and optimization to ameliorate the method and overcome some of the limitations of this technique.

RRCNN: A novel signal decomposition approach based on recurrent residue convolutional neural network

The decomposition of non-stationary signals is an important and challenging task in the field of signal time-frequency analysis. In the recent two decades, many signal decomposition methods led by the empirical mode decomposition, which was pioneered by Huang et al. in 1998, have been proposed by different research groups. However, they still have some limitations. For example, they are generally prone to boundary and mode mixing effects and are not very robust to noise. Inspired by the successful applications of deep learning in fields like image processing and natural language processing, and given the lack in the literature of works in which deep learning techniques are used directly to decompose non-stationary signals into simple oscillatory components, we use the convolutional neural network, residual structure and nonlinear activation function to compute in an innovative way the local average of the signal, and study a new non-stationary signal decomposition method under the framework of deep learning. We discuss the training process of the proposed model and study the convergence analysis of the learning algorithm. In the experiments, we evaluate the performance of the proposed model from two points of view: the calculation of the local average and the signal decomposition. Furthermore, we study the mode mixing, noise interference, and orthogonality properties of the decomposed components produced by the proposed method. All results show that the proposed model allows for better handling boundary effect, mode mixing effect, robustness, and the orthogonality of the decomposed components than existing methods.

Hyperspectral Chemical Plume Detection Algorithms Based On Multidimensional Iterative Filtering Decomposition

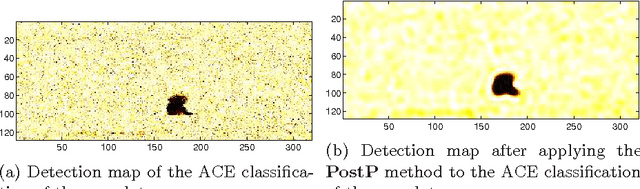
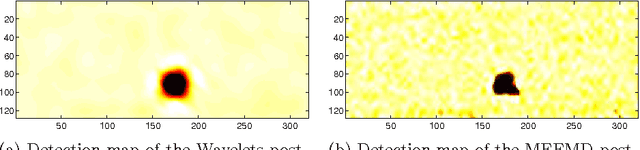
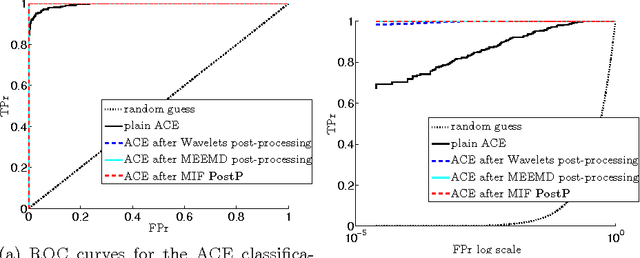
Chemicals released in the air can be extremely dangerous for human beings and the environment. Hyperspectral images can be used to identify chemical plumes, however the task can be extremely challenging. Assuming we know a priori that some chemical plume, with a known frequency spectrum, has been photographed using a hyperspectral sensor, we can use standard techniques like the so called matched filter or adaptive cosine estimator, plus a properly chosen threshold value, to identify the position of the chemical plume. However, due to noise and sensors fault, the accurate identification of chemical pixels is not easy even in this apparently simple situation. In this paper we present a post-processing tool that, in a completely adaptive and data driven fashion, allows to improve the performance of any classification methods in identifying the boundaries of a plume. This is done using the Multidimensional Iterative Filtering (MIF) algorithm (arXiv:1411.6051, arXiv:1507.07173), which is a non-stationary signal decomposition method like the pioneering Empirical Mode Decomposition (EMD) method. Moreover, based on the MIF technique, we propose also a pre-processing method that allows to decorrelate and mean-center a hyperspectral dataset. The Cosine Similarity measure, which often fails in practice, appears to become a successful and outperforming classifier when equipped with such pre-processing method. We show some examples of the proposed methods when applied to real life problems.