LAMA: Stable Dual-Domain Deep Reconstruction For Sparse-View CT

Inverse problems arise in many applications, especially tomographic imaging. We develop a Learned Alternating Minimization Algorithm (LAMA) to solve such problems via two-block optimization by synergizing data-driven and classical techniques with proven convergence. LAMA is naturally induced by a variational model with learnable regularizers in both data and image domains, parameterized as composite functions of neural networks trained with domain-specific data. We allow these regularizers to be nonconvex and nonsmooth to extract features from data effectively. We minimize the overall objective function using Nesterov's smoothing technique and residual learning architecture. It is demonstrated that LAMA reduces network complexity, improves memory efficiency, and enhances reconstruction accuracy, stability, and interpretability. Extensive experiments show that LAMA significantly outperforms state-of-the-art methods on popular benchmark datasets for Computed Tomography.

Approximation of Solution Operators for High-dimensional PDEs

We propose a finite-dimensional control-based method to approximate solution operators for evolutional partial differential equations (PDEs), particularly in high-dimensions. By employing a general reduced-order model, such as a deep neural network, we connect the evolution of the model parameters with trajectories in a corresponding function space. Using the computational technique of neural ordinary differential equation, we learn the control over the parameter space such that from any initial starting point, the controlled trajectories closely approximate the solutions to the PDE. Approximation accuracy is justified for a general class of second-order nonlinear PDEs. Numerical results are presented for several high-dimensional PDEs, including real-world applications to solving Hamilton-Jacobi-Bellman equations. These are demonstrated to show the accuracy and efficiency of the proposed method.

Approximating High-Dimensional Minimal Surfaces with Physics-Informed Neural Networks

In this paper, we compute numerical approximations of the minimal surfaces, an essential type of Partial Differential Equation (PDE), in higher dimensions. Classical methods cannot handle it in this case because of the Curse of Dimensionality, where the computational cost of these methods increases exponentially fast in response to higher problem dimensions, far beyond the computing capacity of any modern supercomputers. Only in the past few years have machine learning researchers been able to mitigate this problem. The solution method chosen here is a model known as a Physics-Informed Neural Network (PINN) which trains a deep neural network (DNN) to solve the minimal surface PDE. It can be scaled up into higher dimensions and trained relatively quickly even on a laptop with no GPU. Due to the inability to view the high-dimension output, our data is presented as snippets of a higher-dimension shape with enough fixed axes so that it is viewable with 3-D graphs. Not only will the functionality of this method be tested, but we will also explore potential limitations in the method's performance.

Learned Alternating Minimization Algorithm for Dual-domain Sparse-View CT Reconstruction

We propose a novel Learned Alternating Minimization Algorithm (LAMA) for dual-domain sparse-view CT image reconstruction. LAMA is naturally induced by a variational model for CT reconstruction with learnable nonsmooth nonconvex regularizers, which are parameterized as composite functions of deep networks in both image and sinogram domains. To minimize the objective of the model, we incorporate the smoothing technique and residual learning architecture into the design of LAMA. We show that LAMA substantially reduces network complexity, improves memory efficiency and reconstruction accuracy, and is provably convergent for reliable reconstructions. Extensive numerical experiments demonstrate that LAMA outperforms existing methods by a wide margin on multiple benchmark CT datasets.

Neural Control of Parametric Solutions for High-dimensional Evolution PDEs

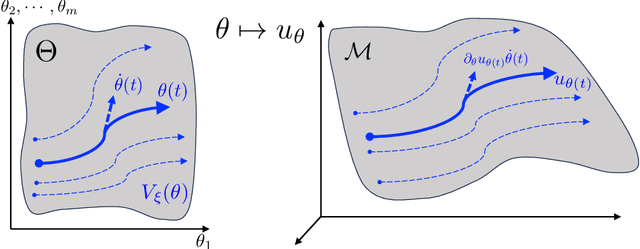
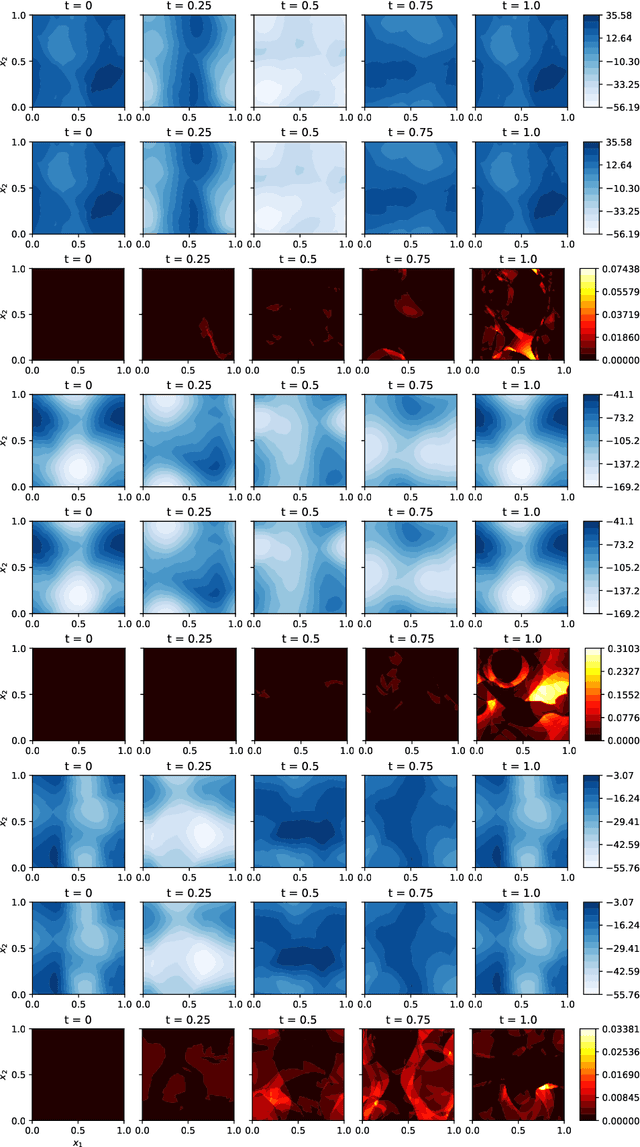
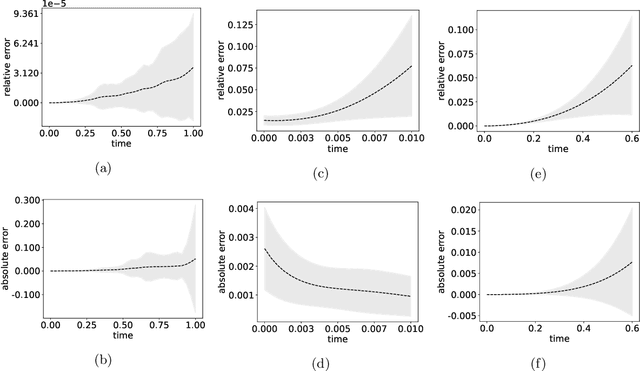
We develop a novel computational framework to approximate solution operators of evolution partial differential equations (PDEs). By employing a general nonlinear reduced-order model, such as a deep neural network, to approximate the solution of a given PDE, we realize that the evolution of the model parameter is a control problem in the parameter space. Based on this observation, we propose to approximate the solution operator of the PDE by learning the control vector field in the parameter space. From any initial value, this control field can steer the parameter to generate a trajectory such that the corresponding reduced-order model solves the PDE. This allows for substantially reduced computational cost to solve the evolution PDE with arbitrary initial conditions. We also develop comprehensive error analysis for the proposed method when solving a large class of semilinear parabolic PDEs. Numerical experiments on different high-dimensional evolution PDEs with various initial conditions demonstrate the promising results of the proposed method.

A Learnable Variational Model for Joint Multimodal MRI Reconstruction and Synthesis

Generating multi-contrasts/modal MRI of the same anatomy enriches diagnostic information but is limited in practice due to excessive data acquisition time. In this paper, we propose a novel deep-learning model for joint reconstruction and synthesis of multi-modal MRI using incomplete k-space data of several source modalities as inputs. The output of our model includes reconstructed images of the source modalities and high-quality image synthesized in the target modality. Our proposed model is formulated as a variational problem that leverages several learnable modality-specific feature extractors and a multimodal synthesis module. We propose a learnable optimization algorithm to solve this model, which induces a multi-phase network whose parameters can be trained using multi-modal MRI data. Moreover, a bilevel-optimization framework is employed for robust parameter training. We demonstrate the effectiveness of our approach using extensive numerical experiments.

Low-rank Matrix Recovery With Unknown Correspondence

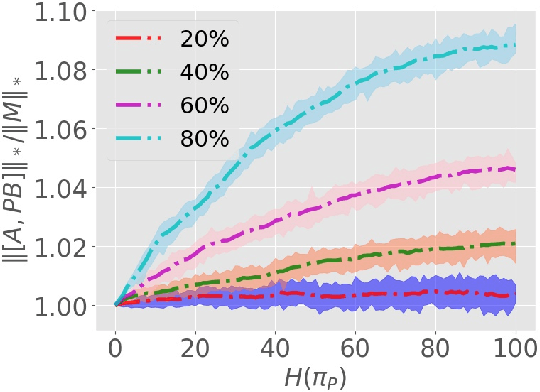
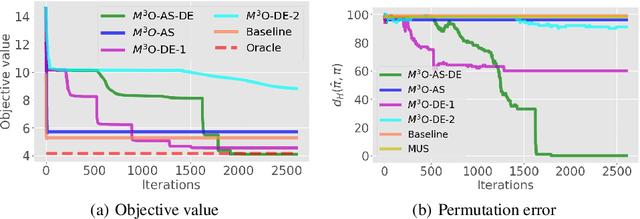
We study a matrix recovery problem with unknown correspondence: given the observation matrix $M_o=[A,\tilde P B]$, where $\tilde P$ is an unknown permutation matrix, we aim to recover the underlying matrix $M=[A,B]$. Such problem commonly arises in many applications where heterogeneous data are utilized and the correspondence among them are unknown, e.g., due to privacy concerns. We show that it is possible to recover $M$ via solving a nuclear norm minimization problem under a proper low-rank condition on $M$, with provable non-asymptotic error bound for the recovery of $M$. We propose an algorithm, $\text{M}^3\text{O}$ (Matrix recovery via Min-Max Optimization) which recasts this combinatorial problem as a continuous minimax optimization problem and solves it by proximal gradient with a Max-Oracle. $\text{M}^3\text{O}$ can also be applied to a more general scenario where we have missing entries in $M_o$ and multiple groups of data with distinct unknown correspondence. Experiments on simulated data, the MovieLens 100K dataset and Yale B database show that $\text{M}^3\text{O}$ achieves state-of-the-art performance over several baselines and can recover the ground-truth correspondence with high accuracy.

An Optimization-Based Meta-Learning Model for MRI Reconstruction with Diverse Dataset

Purpose: This work aims at developing a generalizable MRI reconstruction model in the meta-learning framework. The standard benchmarks in meta-learning are challenged by learning on diverse task distributions. The proposed network learns the regularization function in a variational model and reconstructs MR images with various under-sampling ratios or patterns that may or may not be seen in the training data by leveraging a heterogeneous dataset. Methods: We propose an unrolling network induced by learnable optimization algorithms (LOA) for solving our nonconvex nonsmooth variational model for MRI reconstruction. In this model, the learnable regularization function contains a task-invariant common feature encoder and task-specific learner represented by a shallow network. To train the network we split the training data into two parts: training and validation, and introduce a bilevel optimization algorithm. The lower-level optimization trains task-invariant parameters for the feature encoder with fixed parameters of the task-specific learner on the training dataset, and the upper-level optimizes the parameters of the task-specific learner on the validation dataset. Results: The average PSNR increases significantly compared to the network trained through conventional supervised learning on the seen CS ratios. We test the result of quick adaption on the unseen tasks after meta-training and in the meanwhile saving half of the training time; Conclusion: We proposed a meta-learning framework consisting of the base network architecture, design of regularization, and bi-level optimization-based training. The network inherits the convergence property of the LOA and interpretation of the variational model. The generalization ability is improved by the designated regularization and bilevel optimization-based training algorithm.

Lyapunov-Net: A Deep Neural Network Architecture for Lyapunov Function Approximation

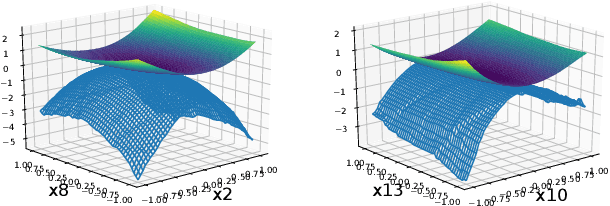
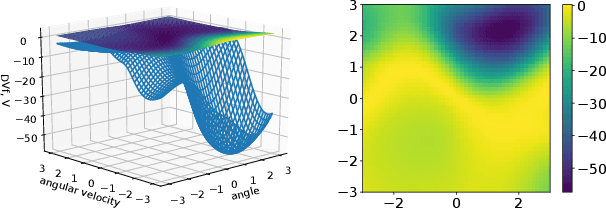
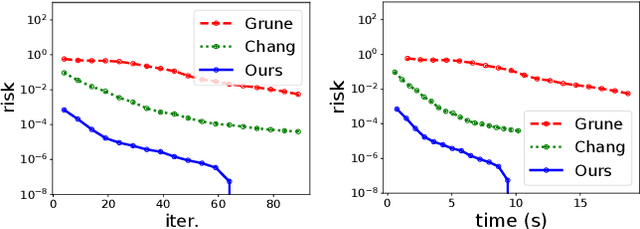
We develop a versatile deep neural network architecture, called Lyapunov-Net, to approximate Lyapunov functions of dynamical systems in high dimensions. Lyapunov-Net guarantees positive definiteness, and thus it can be easily trained to satisfy the negative orbital derivative condition, which only renders a single term in the empirical risk function in practice. This significantly reduces the number of hyper-parameters compared to existing methods. We also provide theoretical justifications on the approximation power of Lyapunov-Net and its complexity bounds. We demonstrate the efficiency of the proposed method on nonlinear dynamical systems involving up to 30-dimensional state spaces, and show that the proposed approach significantly outperforms the state-of-the-art methods.

An Optimal Control Framework for Joint-channel Parallel MRI Reconstruction without Coil Sensitivities

Goal: This work aims at developing a novel calibration-free fast parallel MRI (pMRI) reconstruction method incorporate with discrete-time optimal control framework. The reconstruction model is designed to learn a regularization that combines channels and extracts features by leveraging the information sharing among channels of multi-coil images. We propose to recover both magnitude and phase information by taking advantage of structured multiplayer convolutional networks in image and Fourier spaces. Methods: We develop a novel variational model with a learnable objective function that integrates an adaptive multi-coil image combination operator and effective image regularization in the image and Fourier spaces. We cast the reconstruction network as a structured discrete-time optimal control system, resulting in an optimal control formulation of parameter training where the parameters of the objective function play the role of control variables. We demonstrate that the Lagrangian method for solving the control problem is equivalent to back-propagation, ensuring the local convergence of the training algorithm. Results: We conduct a large number of numerical experiments of the proposed method with comparisons to several state-of-the-art pMRI reconstruction networks on real pMRI datasets. The numerical results demonstrate the promising performance of the proposed method evidently. Conclusion: The proposed method provides a general deep network design and training framework for efficient joint-channel pMRI reconstruction. Significance: By learning multi-coil image combination operator and performing regularizations in both image domain and k-space domain, the proposed method achieves a highly efficient image reconstruction network for pMRI.