Lyapunov-Net: A Deep Neural Network Architecture for Lyapunov Function Approximation
Paper and Code
Sep 27, 2021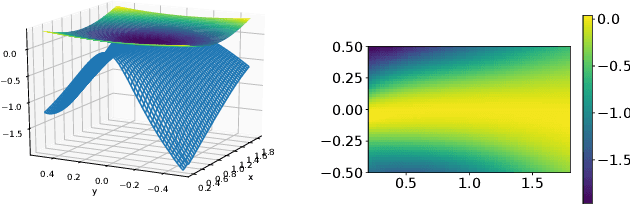
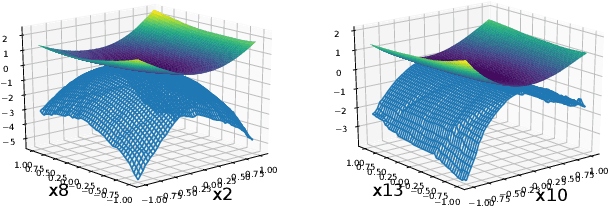
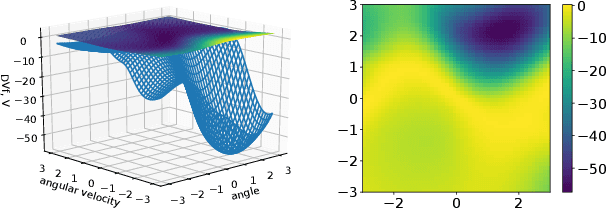
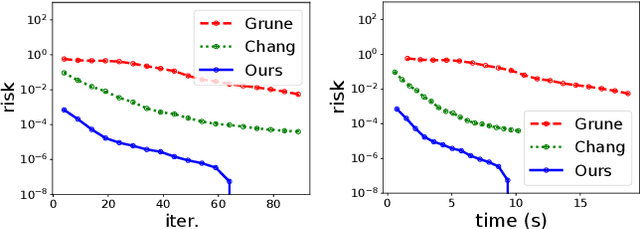
We develop a versatile deep neural network architecture, called Lyapunov-Net, to approximate Lyapunov functions of dynamical systems in high dimensions. Lyapunov-Net guarantees positive definiteness, and thus it can be easily trained to satisfy the negative orbital derivative condition, which only renders a single term in the empirical risk function in practice. This significantly reduces the number of hyper-parameters compared to existing methods. We also provide theoretical justifications on the approximation power of Lyapunov-Net and its complexity bounds. We demonstrate the efficiency of the proposed method on nonlinear dynamical systems involving up to 30-dimensional state spaces, and show that the proposed approach significantly outperforms the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge