Hamiltonian Theory and Computation of Optimal Probability Density Control in High Dimensions

We develop a general theoretical framework for optimal probability density control and propose a numerical algorithm that is scalable to solve the control problem in high dimensions. Specifically, we establish the Pontryagin Maximum Principle (PMP) for optimal density control and construct the Hamilton-Jacobi-Bellman (HJB) equation of the value functional through rigorous derivations without any concept from Wasserstein theory. To solve the density control problem numerically, we propose to use reduced-order models, such as deep neural networks (DNNs), to parameterize the control vector-field and the adjoint function, which allows us to tackle problems defined on high-dimensional state spaces. We also prove several convergence properties of the proposed algorithm. Numerical results demonstrate promising performances of our algorithm on a variety of density control problems with obstacles and nonlinear interaction challenges in high dimensions.

Approximation of Solution Operators for High-dimensional PDEs

We propose a finite-dimensional control-based method to approximate solution operators for evolutional partial differential equations (PDEs), particularly in high-dimensions. By employing a general reduced-order model, such as a deep neural network, we connect the evolution of the model parameters with trajectories in a corresponding function space. Using the computational technique of neural ordinary differential equation, we learn the control over the parameter space such that from any initial starting point, the controlled trajectories closely approximate the solutions to the PDE. Approximation accuracy is justified for a general class of second-order nonlinear PDEs. Numerical results are presented for several high-dimensional PDEs, including real-world applications to solving Hamilton-Jacobi-Bellman equations. These are demonstrated to show the accuracy and efficiency of the proposed method.

Neural Control of Parametric Solutions for High-dimensional Evolution PDEs

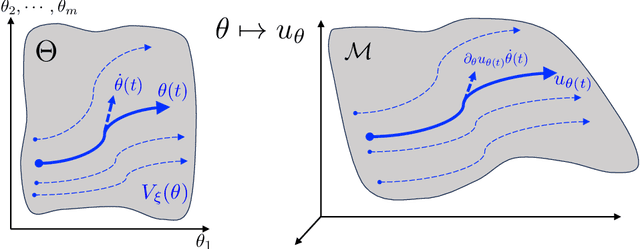
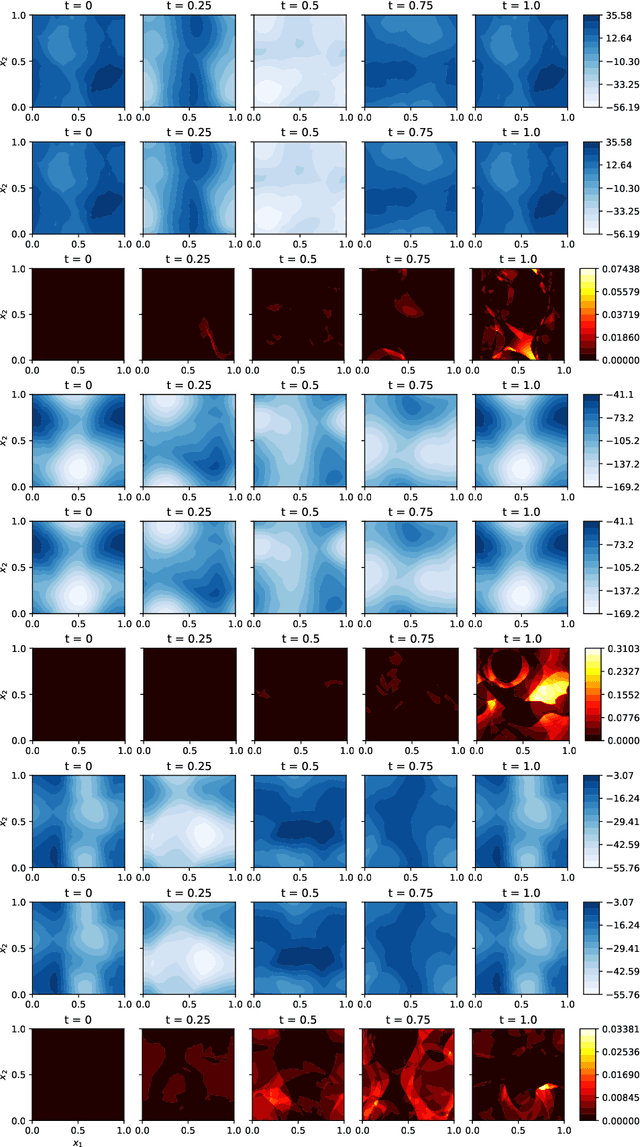
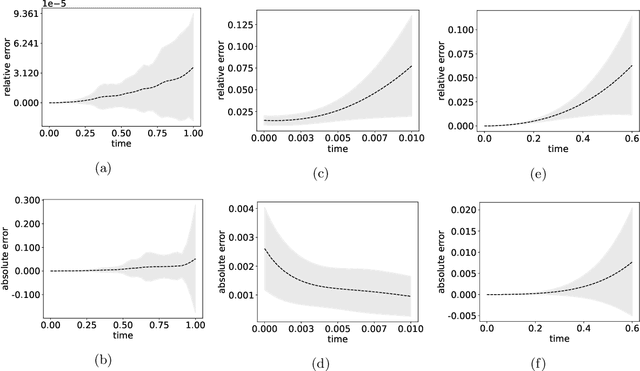
We develop a novel computational framework to approximate solution operators of evolution partial differential equations (PDEs). By employing a general nonlinear reduced-order model, such as a deep neural network, to approximate the solution of a given PDE, we realize that the evolution of the model parameter is a control problem in the parameter space. Based on this observation, we propose to approximate the solution operator of the PDE by learning the control vector field in the parameter space. From any initial value, this control field can steer the parameter to generate a trajectory such that the corresponding reduced-order model solves the PDE. This allows for substantially reduced computational cost to solve the evolution PDE with arbitrary initial conditions. We also develop comprehensive error analysis for the proposed method when solving a large class of semilinear parabolic PDEs. Numerical experiments on different high-dimensional evolution PDEs with various initial conditions demonstrate the promising results of the proposed method.

Lyapunov-Net: A Deep Neural Network Architecture for Lyapunov Function Approximation

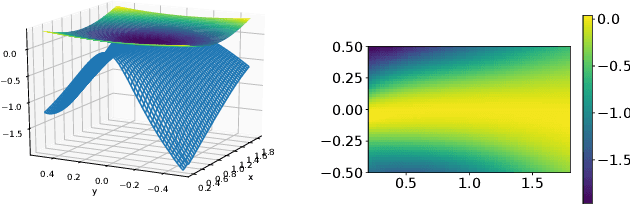
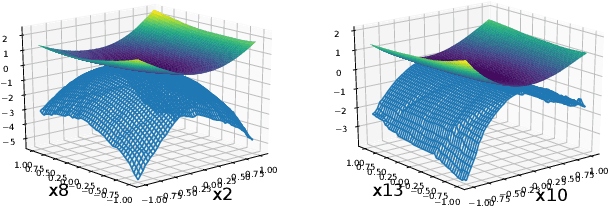
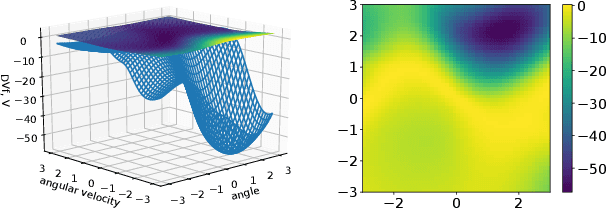
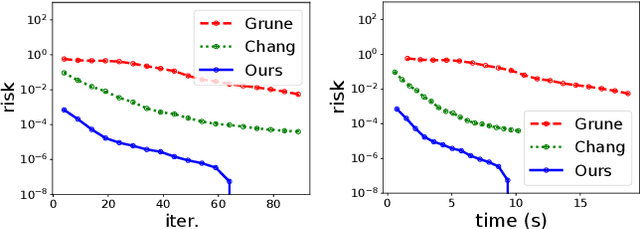
We develop a versatile deep neural network architecture, called Lyapunov-Net, to approximate Lyapunov functions of dynamical systems in high dimensions. Lyapunov-Net guarantees positive definiteness, and thus it can be easily trained to satisfy the negative orbital derivative condition, which only renders a single term in the empirical risk function in practice. This significantly reduces the number of hyper-parameters compared to existing methods. We also provide theoretical justifications on the approximation power of Lyapunov-Net and its complexity bounds. We demonstrate the efficiency of the proposed method on nonlinear dynamical systems involving up to 30-dimensional state spaces, and show that the proposed approach significantly outperforms the state-of-the-art methods.