A Learned Proximal Alternating Minimization Algorithm and Its Induced Network for a Class of Two-block Nonconvex and Nonsmooth Optimization

This work proposes a general learned proximal alternating minimization algorithm, LPAM, for solving learnable two-block nonsmooth and nonconvex optimization problems. We tackle the nonsmoothness by an appropriate smoothing technique with automatic diminishing smoothing effect. For smoothed nonconvex problems we modify the proximal alternating linearized minimization (PALM) scheme by incorporating the residual learning architecture, which has proven to be highly effective in deep network training, and employing the block coordinate decent (BCD) iterates as a safeguard for the convergence of the algorithm. We prove that there is a subsequence of the iterates generated by LPAM, which has at least one accumulation point and each accumulation point is a Clarke stationary point. Our method is widely applicable as one can employ various learning problems formulated as two-block optimizations, and is also easy to be extended for solving multi-block nonsmooth and nonconvex optimization problems. The network, whose architecture follows the LPAM exactly, namely LPAM-net, inherits the convergence properties of the algorithm to make the network interpretable. As an example application of LPAM-net, we present the numerical and theoretical results on the application of LPAM-net for joint multi-modal MRI reconstruction with significantly under-sampled k-space data. The experimental results indicate the proposed LPAM-net is parameter-efficient and has favourable performance in comparison with some state-of-the-art methods.

LAMA: Stable Dual-Domain Deep Reconstruction For Sparse-View CT

Inverse problems arise in many applications, especially tomographic imaging. We develop a Learned Alternating Minimization Algorithm (LAMA) to solve such problems via two-block optimization by synergizing data-driven and classical techniques with proven convergence. LAMA is naturally induced by a variational model with learnable regularizers in both data and image domains, parameterized as composite functions of neural networks trained with domain-specific data. We allow these regularizers to be nonconvex and nonsmooth to extract features from data effectively. We minimize the overall objective function using Nesterov's smoothing technique and residual learning architecture. It is demonstrated that LAMA reduces network complexity, improves memory efficiency, and enhances reconstruction accuracy, stability, and interpretability. Extensive experiments show that LAMA significantly outperforms state-of-the-art methods on popular benchmark datasets for Computed Tomography.

Deep unrolled primal dual network for TOF-PET list-mode image reconstruction

Time-of-flight (TOF) information provides more accurate location data for annihilation photons, thereby enhancing the quality of PET reconstruction images and reducing noise. List-mode reconstruction has a significant advantage in handling TOF information. However, current advanced TOF PET list-mode reconstruction algorithms still require improvements when dealing with low-count data. Deep learning algorithms have shown promising results in PET image reconstruction. Nevertheless, the incorporation of TOF information poses significant challenges related to the storage space required by deep learning methods, particularly for the advanced deep unrolled methods. In this study, we propose a deep unrolled primal dual network for TOF-PET list-mode reconstruction. The network is unrolled into multiple phases, with each phase comprising a dual network for list-mode domain updates and a primal network for image domain updates. We utilize CUDA for parallel acceleration and computation of the system matrix for TOF list-mode data, and we adopt a dynamic access strategy to mitigate memory consumption. Reconstructed images of different TOF resolutions and different count levels show that the proposed method outperforms the LM-OSEM, LM-EMTV, LM-SPDHG,LM-SPDHG-TV and FastPET method in both visually and quantitative analysis. These results demonstrate the potential application of deep unrolled methods for TOF-PET list-mode data and show better performance than current mainstream TOF-PET list-mode reconstruction algorithms, providing new insights for the application of deep learning methods in TOF list-mode data. The codes for this work are available at https://github.com/RickHH/LMPDnet

Learned Alternating Minimization Algorithm for Dual-domain Sparse-View CT Reconstruction

We propose a novel Learned Alternating Minimization Algorithm (LAMA) for dual-domain sparse-view CT image reconstruction. LAMA is naturally induced by a variational model for CT reconstruction with learnable nonsmooth nonconvex regularizers, which are parameterized as composite functions of deep networks in both image and sinogram domains. To minimize the objective of the model, we incorporate the smoothing technique and residual learning architecture into the design of LAMA. We show that LAMA substantially reduces network complexity, improves memory efficiency and reconstruction accuracy, and is provably convergent for reliable reconstructions. Extensive numerical experiments demonstrate that LAMA outperforms existing methods by a wide margin on multiple benchmark CT datasets.

DULDA: Dual-domain Unsupervised Learned Descent Algorithm for PET image reconstruction

Deep learning based PET image reconstruction methods have achieved promising results recently. However, most of these methods follow a supervised learning paradigm, which rely heavily on the availability of high-quality training labels. In particular, the long scanning time required and high radiation exposure associated with PET scans make obtaining this labels impractical. In this paper, we propose a dual-domain unsupervised PET image reconstruction method based on learned decent algorithm, which reconstructs high-quality PET images from sinograms without the need for image labels. Specifically, we unroll the proximal gradient method with a learnable l2,1 norm for PET image reconstruction problem. The training is unsupervised, using measurement domain loss based on deep image prior as well as image domain loss based on rotation equivariance property. The experimental results domonstrate the superior performance of proposed method compared with maximum likelihood expectation maximazation (MLEM), total-variation regularized EM (EM-TV) and deep image prior based method (DIP).

STPDnet: Spatial-temporal convolutional primal dual network for dynamic PET image reconstruction

Dynamic positron emission tomography (dPET) image reconstruction is extremely challenging due to the limited counts received in individual frame. In this paper, we propose a spatial-temporal convolutional primal dual network (STPDnet) for dynamic PET image reconstruction. Both spatial and temporal correlations are encoded by 3D convolution operators. The physical projection of PET is embedded in the iterative learning process of the network, which provides the physical constraints and enhances interpretability. The experiments of real rat scan data have shown that the proposed method can achieve substantial noise reduction in both temporal and spatial domains and outperform the maximum likelihood expectation maximization (MLEM), spatial-temporal kernel method (KEM-ST), DeepPET and Learned Primal Dual (LPD).

A Learnable Variational Model for Joint Multimodal MRI Reconstruction and Synthesis

Generating multi-contrasts/modal MRI of the same anatomy enriches diagnostic information but is limited in practice due to excessive data acquisition time. In this paper, we propose a novel deep-learning model for joint reconstruction and synthesis of multi-modal MRI using incomplete k-space data of several source modalities as inputs. The output of our model includes reconstructed images of the source modalities and high-quality image synthesized in the target modality. Our proposed model is formulated as a variational problem that leverages several learnable modality-specific feature extractors and a multimodal synthesis module. We propose a learnable optimization algorithm to solve this model, which induces a multi-phase network whose parameters can be trained using multi-modal MRI data. Moreover, a bilevel-optimization framework is employed for robust parameter training. We demonstrate the effectiveness of our approach using extensive numerical experiments.

An Optimization-Based Meta-Learning Model for MRI Reconstruction with Diverse Dataset

Purpose: This work aims at developing a generalizable MRI reconstruction model in the meta-learning framework. The standard benchmarks in meta-learning are challenged by learning on diverse task distributions. The proposed network learns the regularization function in a variational model and reconstructs MR images with various under-sampling ratios or patterns that may or may not be seen in the training data by leveraging a heterogeneous dataset. Methods: We propose an unrolling network induced by learnable optimization algorithms (LOA) for solving our nonconvex nonsmooth variational model for MRI reconstruction. In this model, the learnable regularization function contains a task-invariant common feature encoder and task-specific learner represented by a shallow network. To train the network we split the training data into two parts: training and validation, and introduce a bilevel optimization algorithm. The lower-level optimization trains task-invariant parameters for the feature encoder with fixed parameters of the task-specific learner on the training dataset, and the upper-level optimizes the parameters of the task-specific learner on the validation dataset. Results: The average PSNR increases significantly compared to the network trained through conventional supervised learning on the seen CS ratios. We test the result of quick adaption on the unseen tasks after meta-training and in the meanwhile saving half of the training time; Conclusion: We proposed a meta-learning framework consisting of the base network architecture, design of regularization, and bi-level optimization-based training. The network inherits the convergence property of the LOA and interpretation of the variational model. The generalization ability is improved by the designated regularization and bilevel optimization-based training algorithm.

An Optimal Control Framework for Joint-channel Parallel MRI Reconstruction without Coil Sensitivities

Goal: This work aims at developing a novel calibration-free fast parallel MRI (pMRI) reconstruction method incorporate with discrete-time optimal control framework. The reconstruction model is designed to learn a regularization that combines channels and extracts features by leveraging the information sharing among channels of multi-coil images. We propose to recover both magnitude and phase information by taking advantage of structured multiplayer convolutional networks in image and Fourier spaces. Methods: We develop a novel variational model with a learnable objective function that integrates an adaptive multi-coil image combination operator and effective image regularization in the image and Fourier spaces. We cast the reconstruction network as a structured discrete-time optimal control system, resulting in an optimal control formulation of parameter training where the parameters of the objective function play the role of control variables. We demonstrate that the Lagrangian method for solving the control problem is equivalent to back-propagation, ensuring the local convergence of the training algorithm. Results: We conduct a large number of numerical experiments of the proposed method with comparisons to several state-of-the-art pMRI reconstruction networks on real pMRI datasets. The numerical results demonstrate the promising performance of the proposed method evidently. Conclusion: The proposed method provides a general deep network design and training framework for efficient joint-channel pMRI reconstruction. Significance: By learning multi-coil image combination operator and performing regularizations in both image domain and k-space domain, the proposed method achieves a highly efficient image reconstruction network for pMRI.

Provably Convergent Learned Inexact Descent Algorithm for Low-Dose CT Reconstruction

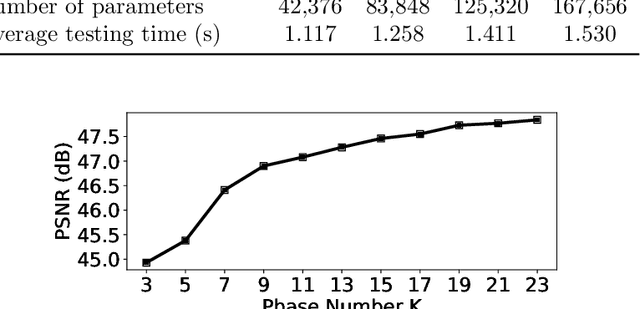
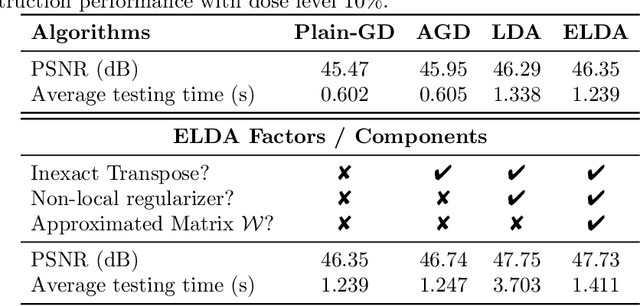
We propose a provably convergent method, called Efficient Learned Descent Algorithm (ELDA), for low-dose CT (LDCT) reconstruction. ELDA is a highly interpretable neural network architecture with learned parameters and meanwhile retains convergence guarantee as classical optimization algorithms. To improve reconstruction quality, the proposed ELDA also employs a new non-local feature mapping and an associated regularizer. We compare ELDA with several state-of-the-art deep image methods, such as RED-CNN and Learned Primal-Dual, on a set of LDCT reconstruction problems. Numerical experiments demonstrate improvement of reconstruction quality using ELDA with merely 19 layers, suggesting the promising performance of ELDA in solution accuracy and parameter efficiency.