An Immediate Update Strategy of Multi-State Constraint Kalman Filter

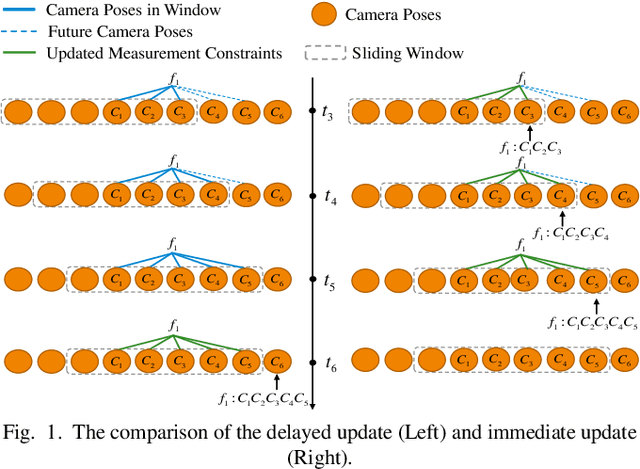
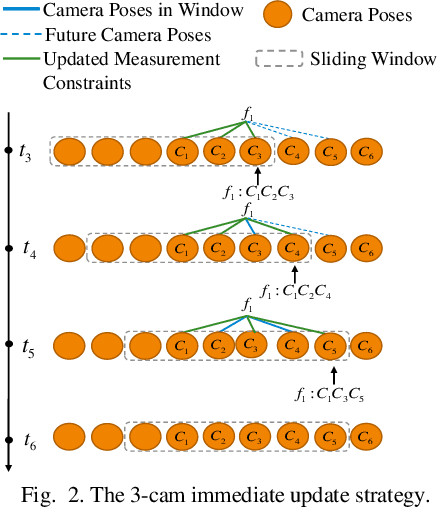
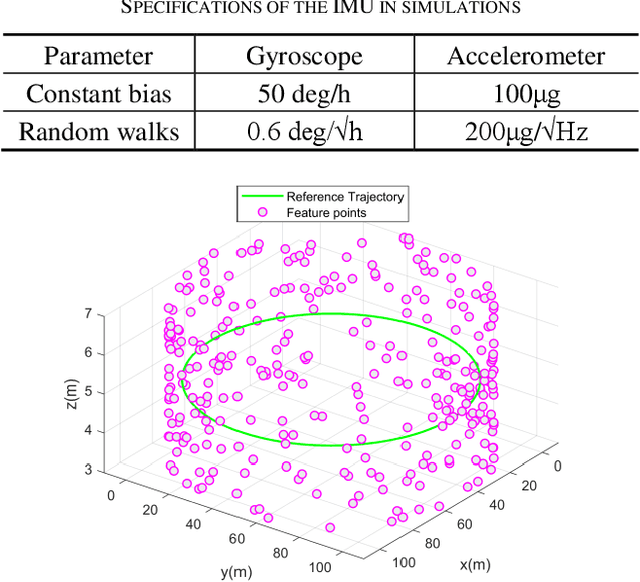
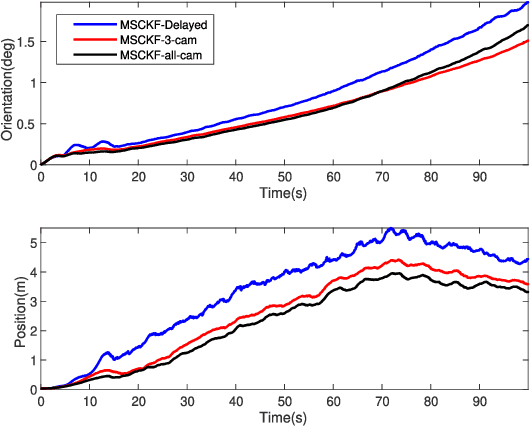
The lightweight Multi-state Constraint Kalman Filter (MSCKF) has been well-known for its high efficiency, in which the delayed update has been usually adopted since its proposal. This work investigates the immediate update strategy of MSCKF based on timely reconstructed 3D feature points and measurement constraints. The differences between the delayed update and the immediate update are theoretically analyzed in detail. It is found that the immediate update helps construct more observation constraints and employ more filtering updates than the delayed update, which improves the linearization point of the measurement model and therefore enhances the estimation accuracy. Numerical simulations and experiments show that the immediate update strategy significantly enhances MSCKF even with a small amount of feature observations.

LAMA: Stable Dual-Domain Deep Reconstruction For Sparse-View CT

Inverse problems arise in many applications, especially tomographic imaging. We develop a Learned Alternating Minimization Algorithm (LAMA) to solve such problems via two-block optimization by synergizing data-driven and classical techniques with proven convergence. LAMA is naturally induced by a variational model with learnable regularizers in both data and image domains, parameterized as composite functions of neural networks trained with domain-specific data. We allow these regularizers to be nonconvex and nonsmooth to extract features from data effectively. We minimize the overall objective function using Nesterov's smoothing technique and residual learning architecture. It is demonstrated that LAMA reduces network complexity, improves memory efficiency, and enhances reconstruction accuracy, stability, and interpretability. Extensive experiments show that LAMA significantly outperforms state-of-the-art methods on popular benchmark datasets for Computed Tomography.

Learned Alternating Minimization Algorithm for Dual-domain Sparse-View CT Reconstruction

We propose a novel Learned Alternating Minimization Algorithm (LAMA) for dual-domain sparse-view CT image reconstruction. LAMA is naturally induced by a variational model for CT reconstruction with learnable nonsmooth nonconvex regularizers, which are parameterized as composite functions of deep networks in both image and sinogram domains. To minimize the objective of the model, we incorporate the smoothing technique and residual learning architecture into the design of LAMA. We show that LAMA substantially reduces network complexity, improves memory efficiency and reconstruction accuracy, and is provably convergent for reliable reconstructions. Extensive numerical experiments demonstrate that LAMA outperforms existing methods by a wide margin on multiple benchmark CT datasets.

A Learnable Variational Model for Joint Multimodal MRI Reconstruction and Synthesis

Generating multi-contrasts/modal MRI of the same anatomy enriches diagnostic information but is limited in practice due to excessive data acquisition time. In this paper, we propose a novel deep-learning model for joint reconstruction and synthesis of multi-modal MRI using incomplete k-space data of several source modalities as inputs. The output of our model includes reconstructed images of the source modalities and high-quality image synthesized in the target modality. Our proposed model is formulated as a variational problem that leverages several learnable modality-specific feature extractors and a multimodal synthesis module. We propose a learnable optimization algorithm to solve this model, which induces a multi-phase network whose parameters can be trained using multi-modal MRI data. Moreover, a bilevel-optimization framework is employed for robust parameter training. We demonstrate the effectiveness of our approach using extensive numerical experiments.

An Optimization-Based Meta-Learning Model for MRI Reconstruction with Diverse Dataset

Purpose: This work aims at developing a generalizable MRI reconstruction model in the meta-learning framework. The standard benchmarks in meta-learning are challenged by learning on diverse task distributions. The proposed network learns the regularization function in a variational model and reconstructs MR images with various under-sampling ratios or patterns that may or may not be seen in the training data by leveraging a heterogeneous dataset. Methods: We propose an unrolling network induced by learnable optimization algorithms (LOA) for solving our nonconvex nonsmooth variational model for MRI reconstruction. In this model, the learnable regularization function contains a task-invariant common feature encoder and task-specific learner represented by a shallow network. To train the network we split the training data into two parts: training and validation, and introduce a bilevel optimization algorithm. The lower-level optimization trains task-invariant parameters for the feature encoder with fixed parameters of the task-specific learner on the training dataset, and the upper-level optimizes the parameters of the task-specific learner on the validation dataset. Results: The average PSNR increases significantly compared to the network trained through conventional supervised learning on the seen CS ratios. We test the result of quick adaption on the unseen tasks after meta-training and in the meanwhile saving half of the training time; Conclusion: We proposed a meta-learning framework consisting of the base network architecture, design of regularization, and bi-level optimization-based training. The network inherits the convergence property of the LOA and interpretation of the variational model. The generalization ability is improved by the designated regularization and bilevel optimization-based training algorithm.

Provably Convergent Learned Inexact Descent Algorithm for Low-Dose CT Reconstruction

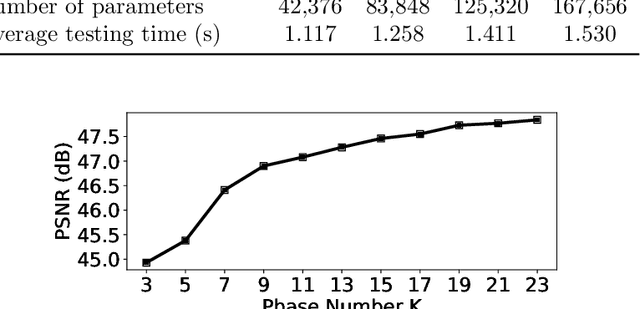
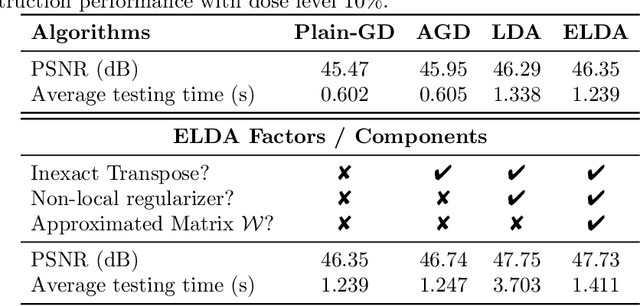
We propose a provably convergent method, called Efficient Learned Descent Algorithm (ELDA), for low-dose CT (LDCT) reconstruction. ELDA is a highly interpretable neural network architecture with learned parameters and meanwhile retains convergence guarantee as classical optimization algorithms. To improve reconstruction quality, the proposed ELDA also employs a new non-local feature mapping and an associated regularizer. We compare ELDA with several state-of-the-art deep image methods, such as RED-CNN and Learned Primal-Dual, on a set of LDCT reconstruction problems. Numerical experiments demonstrate improvement of reconstruction quality using ELDA with merely 19 layers, suggesting the promising performance of ELDA in solution accuracy and parameter efficiency.

Multiscale Detection of Cancerous Tissue in High Resolution Slide Scans

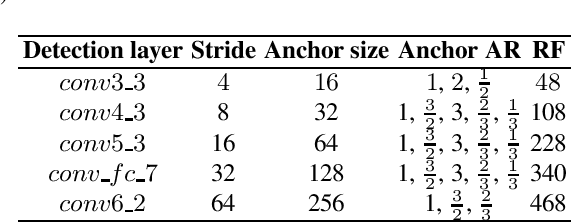
We present an algorithm for multi-scale tumor (chimeric cell) detection in high resolution slide scans. The broad range of tumor sizes in our dataset pose a challenge for current Convolutional Neural Networks (CNN) which often fail when image features are very small (8 pixels). Our approach modifies the effective receptive field at different layers in a CNN so that objects with a broad range of varying scales can be detected in a single forward pass. We define rules for computing adaptive prior anchor boxes which we show are solvable under the equal proportion interval principle. Two mechanisms in our CNN architecture alleviate the effects of non-discriminative features prevalent in our data - a foveal detection algorithm that incorporates a cascade residual-inception module and a deconvolution module with additional context information. When integrated into a Single Shot MultiBox Detector (SSD), these additions permit more accurate detection of small-scale objects. The results permit efficient real-time analysis of medical images in pathology and related biomedical research fields.

Learnable Descent Algorithm for Nonsmooth Nonconvex Image Reconstruction

We propose a general learning based framework for solving nonsmooth and nonconvex image reconstruction problems. We model the regularization function as the composition of the $l_{2,1}$ norm and a smooth but nonconvex feature mapping parametrized as a deep convolutional neural network. We develop a provably convergent descent-type algorithm to solve the nonsmooth nonconvex minimization problem by leveraging the Nesterov's smoothing technique and the idea of residual learning, and learn the network parameters such that the outputs of the algorithm match the references in training data. Our method is versatile as one can employ various modern network structures into the regularization, and the resulting network inherits the guaranteed convergence of the algorithm. We also show that the proposed network is parameter-efficient and its performance compares favorably to the state-of-the-art methods in a variety of image reconstruction problems in practice.

A Novel Learnable Gradient Descent Type Algorithm for Non-convex Non-smooth Inverse Problems

Optimization algorithms for solving nonconvex inverse problem have attracted significant interests recently. However, existing methods require the nonconvex regularization to be smooth or simple to ensure convergence. In this paper, we propose a novel gradient descent type algorithm, by leveraging the idea of residual learning and Nesterov's smoothing technique, to solve inverse problems consisting of general nonconvex and nonsmooth regularization with provable convergence. Moreover, we develop a neural network architecture intimating this algorithm to learn the nonlinear sparsity transformation adaptively from training data, which also inherits the convergence to accommodate the general nonconvex structure of this learned transformation. Numerical results demonstrate that the proposed network outperforms the state-of-the-art methods on a variety of different image reconstruction problems in terms of efficiency and accuracy.

Extra Proximal-Gradient Inspired Non-local Network

Variational method and deep learning method are two mainstream powerful approaches to solve inverse problems in computer vision. To take advantages of advanced optimization algorithms and powerful representation ability of deep neural networks, we propose a novel deep network for image reconstruction. The architecture of this network is inspired by our proposed accelerated extra proximal gradient algorithm. It is able to incorporate non-local operation to exploit the non-local self-similarity of the images and to learn the nonlinear transform, under which the solution is sparse. All the parameters in our network are learned from minimizing a loss function. Our experimental results show that our network outperforms several state-of-the-art deep networks with almost the same number of learnable parameter.