An Immediate Update Strategy of Multi-State Constraint Kalman Filter

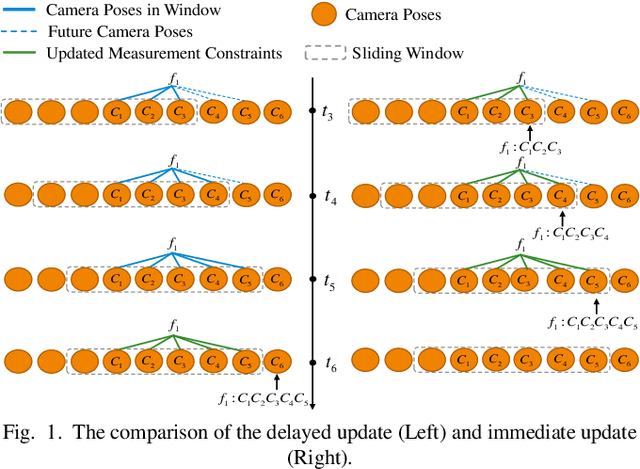
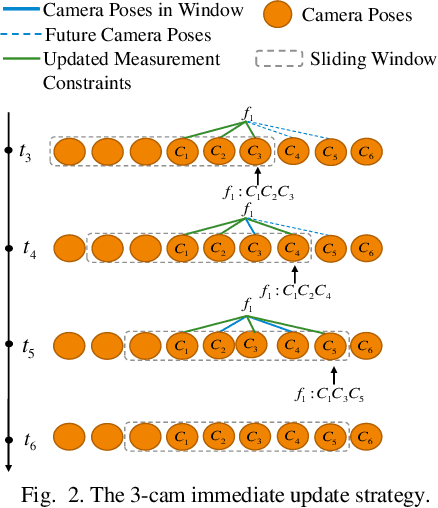
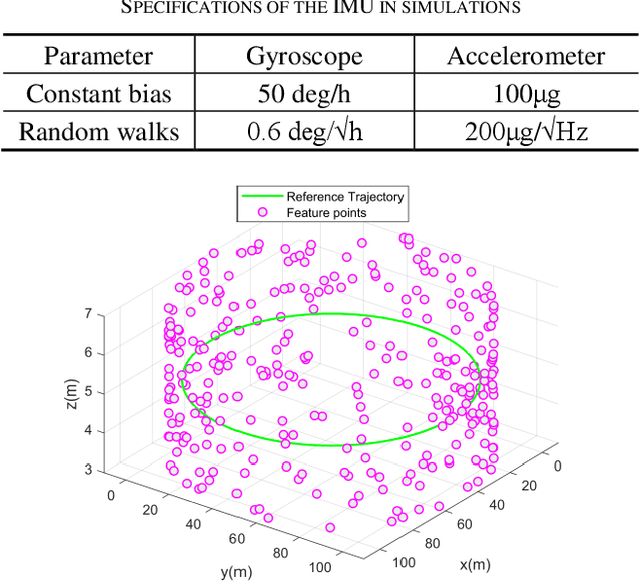
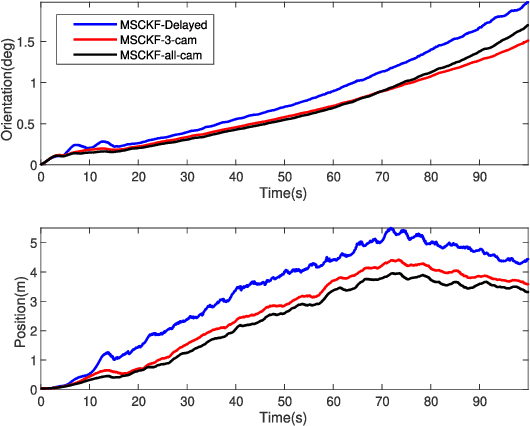
The lightweight Multi-state Constraint Kalman Filter (MSCKF) has been well-known for its high efficiency, in which the delayed update has been usually adopted since its proposal. This work investigates the immediate update strategy of MSCKF based on timely reconstructed 3D feature points and measurement constraints. The differences between the delayed update and the immediate update are theoretically analyzed in detail. It is found that the immediate update helps construct more observation constraints and employ more filtering updates than the delayed update, which improves the linearization point of the measurement model and therefore enhances the estimation accuracy. Numerical simulations and experiments show that the immediate update strategy significantly enhances MSCKF even with a small amount of feature observations.

Visual-inertial state estimation based on Chebyshev polynomial optimization

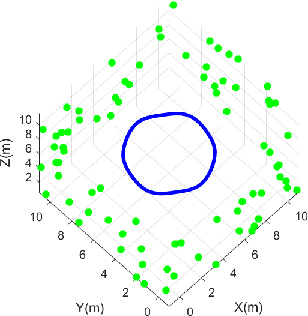
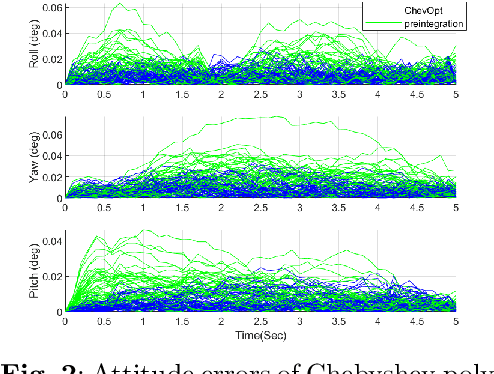
This paper proposes an innovative state estimation method for visual-inertial fusion based on Chebyshev polynomial optimization. Specifically, the pose is modeled as a Chebyshev polynomial of a certain order, and its time derivatives are used to calculate linear acceleration and angular velocity, which, along with inertial measurements, constitute dynamic constraints. This is coupled with a visual measurement model to construct a visual-inertial bundle adjustment formulation. Simulation and public dataset experiments show that the proposed method has better accuracy than the discrete-form preintegration method.

Inertial-based Navigation by Polynomial Optimization: Inertial-Magnetic Attitude Estimation

Inertial-based navigation refers to the navigation methods or systems that have inertial information or sensors as the core part and integrate a spectrum of other kinds of sensors for enhanced performance. Through a series of papers, the authors attempt to explore information blending of inertial-based navigation by a polynomial optimization method. The basic idea is to model rigid motions as finite-order polynomials and then attacks the involved navigation problems by optimally solving their coefficients, taking into considerations the constraints posed by inertial sensors and others. In the current paper, a continuous-time attitude estimation approach is proposed, which transforms the attitude estimation into a constant parameter determination problem by the polynomial optimization. Specifically, the continuous attitude is first approximated by a Chebyshev polynomial, of which the unknown Chebyshev coefficients are determined by minimizing the weighted residuals of initial conditions, dynamics and measurements. We apply the derived estimator to the attitude estimation with the magnetic and inertial sensors. Simulation and field tests show that the estimator has much better stability and faster convergence than the traditional extended Kalman filter does, especially in the challenging large initial state error scenarios.

iNavFIter-M: Matrix Formulation of Functional Iteration for Inertial Navigation Computation

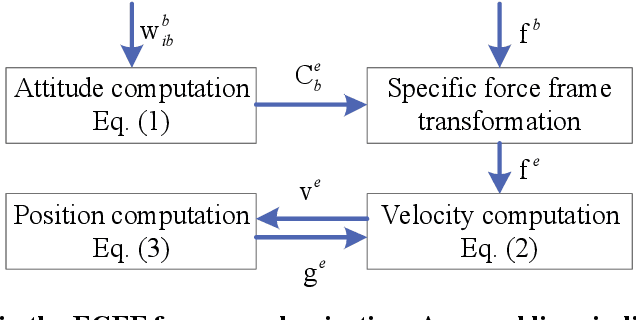
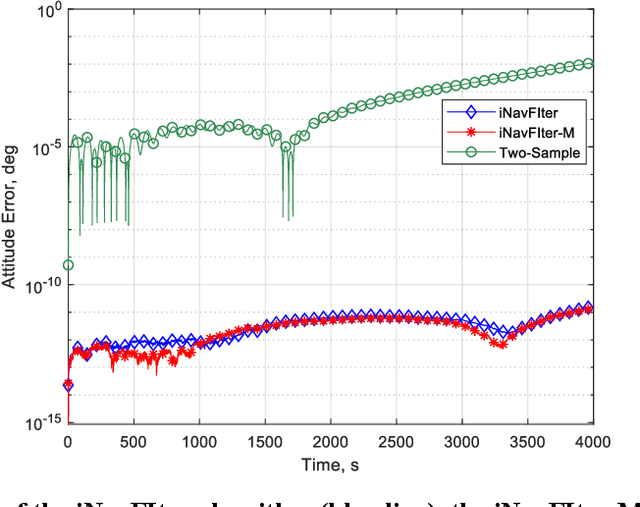
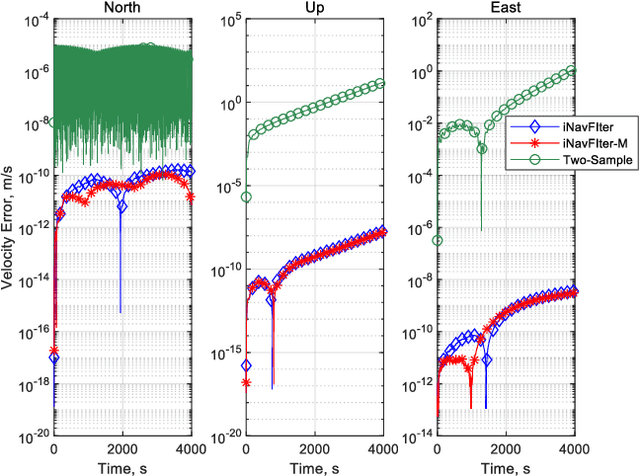
The acquisition of attitude, velocity, and position is an essential task in the field of inertial navigation, achieved by integrating the measurements from inertial sensors. Recently, the ultra-precision inertial navigation computation has been tackled by the functional iteration approach (iNavFIter) that drives the non-commutativity errors almost to the computer truncation error level. This paper proposes a computationally efficient matrix formulation of the functional iteration approach, named the iNavFIter-M. The Chebyshev polynomial coefficients in two consecutive iterations are explicitly connected through the matrix formulation, in contrast to the implicit iterative relationship in the original iNavFIter. By so doing, it allows a straightforward algorithmic implementation and a number of matrix factors can be pre-calculated for more efficient computation. Numerical results demonstrate that the proposed iNavFIter-M algorithm is able to achieve the same high computation accuracy as the original iNavFIter does, at the computational cost comparable to the typical two-sample algorithm. The iNavFIter-M algorithm is also implemented on a FPGA board to demonstrate its potential in real time applications.

ChevOpt: Continuous-time State Estimation by Chebyshev Polynomial Optimization

In this paper, a new framework for continuous-time maximum a posteriori estimation based on the Chebyshev polynomial optimization (ChevOpt) is proposed, which transforms the nonlinear continuous-time state estimation into a problem of constant parameter optimization. Specifically, the time-varying system state is represented by a Chebyshev polynomial and the unknown Chebyshev coefficients are optimized by minimizing the weighted sum of the prior, dynamics and measurements. The proposed ChevOpt is an optimal continuous-time estimation in the least squares sense and needs a batch processing. A recursive sliding-window version is proposed as well to meet the requirement of real-time applications. Comparing with the well-known Gaussian filters, the ChevOpt better resolves the nonlinearities in both dynamics and measurements. Numerical results of demonstrative examples show that the proposed ChevOpt achieves remarkably improved accuracy over the extended/unscented Kalman filters and RTS smoother, close to the Cramer-Rao lower bound.

Attitude Reconstruction from Inertial Measurement: Mitigating Runge Effect for Dynamic Applications

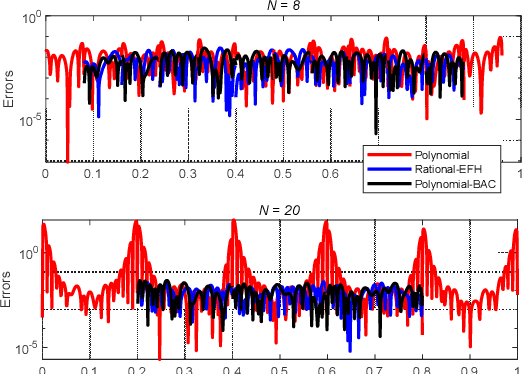
Time-equispaced inertial measurements are practically used as inputs for motion determination. Polynomial interpolation is a common technique of recovering the gyroscope signal but is subject to a fundamentally numerical stability problem due to the Runge effect on equispaced samples. This paper reviews the theoretical results of Runge phenomenon in related areas and proposes a straightforward borrowing-and-cutting (BAC) strategy to depress it. It employs the neighboring samples for higher-order polynomial interpolation but only uses the middle polynomial segment in the actual time interval. The BAC strategy has been incorporated into attitude computation by functional iteration, leading to accuracy benefit of several orders of magnitude under the classical coning motion. It would potentially bring significant benefits to the inertial navigation computation under sustained dynamic motions.