Attitude Reconstruction from Inertial Measurement: Mitigating Runge Effect for Dynamic Applications
Paper and Code
Jul 10, 2021

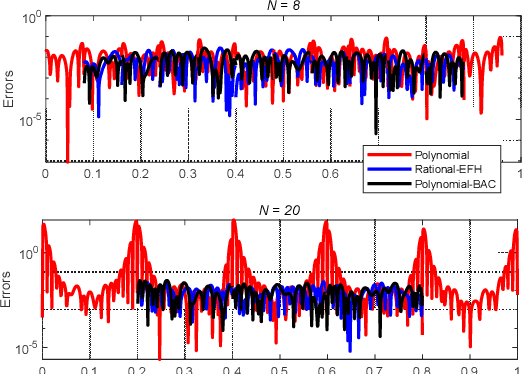

Time-equispaced inertial measurements are practically used as inputs for motion determination. Polynomial interpolation is a common technique of recovering the gyroscope signal but is subject to a fundamentally numerical stability problem due to the Runge effect on equispaced samples. This paper reviews the theoretical results of Runge phenomenon in related areas and proposes a straightforward borrowing-and-cutting (BAC) strategy to depress it. It employs the neighboring samples for higher-order polynomial interpolation but only uses the middle polynomial segment in the actual time interval. The BAC strategy has been incorporated into attitude computation by functional iteration, leading to accuracy benefit of several orders of magnitude under the classical coning motion. It would potentially bring significant benefits to the inertial navigation computation under sustained dynamic motions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge