Structured and Balanced Multi-component and Multi-layer Neural Networks

In this work, we propose a balanced multi-component and multi-layer neural network (MMNN) structure to approximate functions with complex features with both accuracy and efficiency in terms of degrees of freedom and computation cost. The main idea is motivated by a multi-component, each of which can be approximated effectively by a single-layer network, and multi-layer decomposition in a "divide-and-conquer" type of strategy to deal with a complex function. While an easy modification to fully connected neural networks (FCNNs) or multi-layer perceptrons (MLPs) through the introduction of balanced multi-component structures in the network, MMNNs achieve a significant reduction of training parameters, a much more efficient training process, and a much improved accuracy compared to FCNNs or MLPs. Extensive numerical experiments are presented to illustrate the effectiveness of MMNNs in approximating high oscillatory functions and its automatic adaptivity in capturing localized features.

Deep Network Approximation: Beyond ReLU to Diverse Activation Functions

This paper explores the expressive power of deep neural networks for a diverse range of activation functions. An activation function set $\mathscr{A}$ is defined to encompass the majority of commonly used activation functions, such as $\mathtt{ReLU}$, $\mathtt{LeakyReLU}$, $\mathtt{ReLU}^2$, $\mathtt{ELU}$, $\mathtt{SELU}$, $\mathtt{Softplus}$, $\mathtt{GELU}$, $\mathtt{SiLU}$, $\mathtt{Swish}$, $\mathtt{Mish}$, $\mathtt{Sigmoid}$, $\mathtt{Tanh}$, $\mathtt{Arctan}$, $\mathtt{Softsign}$, $\mathtt{dSiLU}$, and $\mathtt{SRS}$. We demonstrate that for any activation function $\varrho\in \mathscr{A}$, a $\mathtt{ReLU}$ network of width $N$ and depth $L$ can be approximated to arbitrary precision by a $\varrho$-activated network of width $6N$ and depth $2L$ on any bounded set. This finding enables the extension of most approximation results achieved with $\mathtt{ReLU}$ networks to a wide variety of other activation functions, at the cost of slightly larger constants.

Why Shallow Networks Struggle with Approximating and Learning High Frequency: A Numerical Study

In this work, a comprehensive numerical study involving analysis and experiments shows why a two-layer neural network has difficulties handling high frequencies in approximation and learning when machine precision and computation cost are important factors in real practice. In particular, the following fundamental computational issues are investigated: (1) the best accuracy one can achieve given a finite machine precision, (2) the computation cost to achieve a given accuracy, and (3) stability with respect to perturbations. The key to the study is the spectral analysis of the corresponding Gram matrix of the activation functions which also shows how the properties of the activation function play a role in the picture.

On Enhancing Expressive Power via Compositions of Single Fixed-Size ReLU Network

This paper studies the expressive power of deep neural networks from the perspective of function compositions. We show that repeated compositions of a single fixed-size ReLU network can produce super expressive power. In particular, we prove by construction that $\mathcal{L}_2\circ \boldsymbol{g}^{\circ r}\circ \boldsymbol{\mathcal{L}}_1$ can approximate $1$-Lipschitz continuous functions on $[0,1]^d$ with an error $\mathcal{O}(r^{-1/d})$, where $\boldsymbol{g}$ is realized by a fixed-size ReLU network, $\boldsymbol{\mathcal{L}}_1$ and $\mathcal{L}_2$ are two affine linear maps matching the dimensions, and $\boldsymbol{g}^{\circ r}$ means the $r$-times composition of $\boldsymbol{g}$. Furthermore, we extend such a result to generic continuous functions on $[0,1]^d$ with the approximation error characterized by the modulus of continuity. Our results reveal that a continuous-depth network generated via a dynamical system has good approximation power even if its dynamics function is time-independent and realized by a fixed-size ReLU network.

A Dual Iterative Refinement Method for Non-rigid Shape Matching

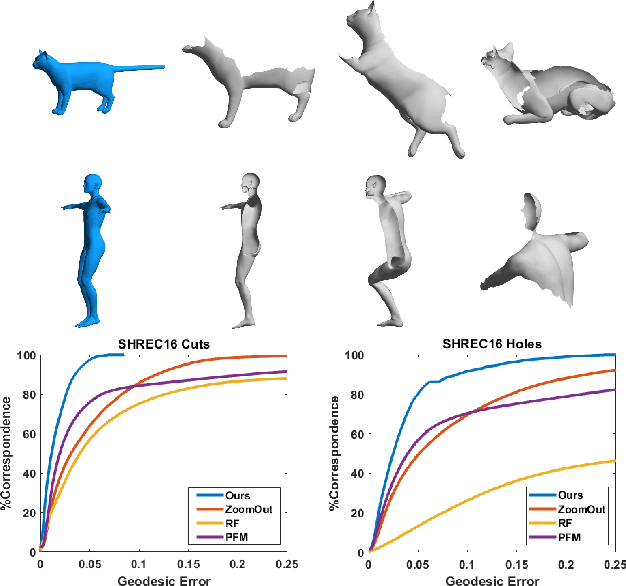
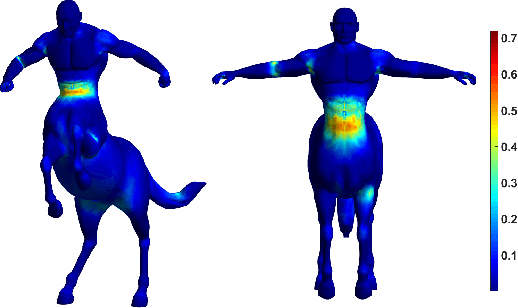
In this work, a simple and efficient dual iterative refinement (DIR) method is proposed for dense correspondence between two nearly isometric shapes. The key idea is to use dual information, such as spatial and spectral, or local and global features, in a complementary and effective way, and extract more accurate information from current iteration to use for the next iteration. In each DIR iteration, starting from current correspondence, a zoom-in process at each point is used to select well matched anchor pairs by a local mapping distortion criterion. These selected anchor pairs are then used to align spectral features (or other appropriate global features) whose dimension adaptively matches the capacity of the selected anchor pairs. Thanks to the effective combination of complementary information in a data-adaptive way, DIR is not only efficient but also robust to render accurate results within a few iterations. By choosing appropriate dual features, DIR has the flexibility to handle patch and partial matching as well. Extensive experiments on various data sets demonstrate the superiority of DIR over other state-of-the-art methods in terms of both accuracy and efficiency.

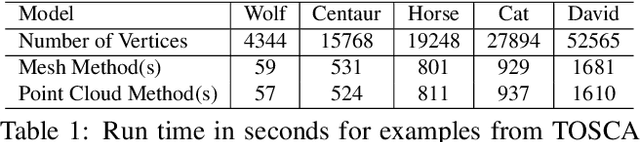
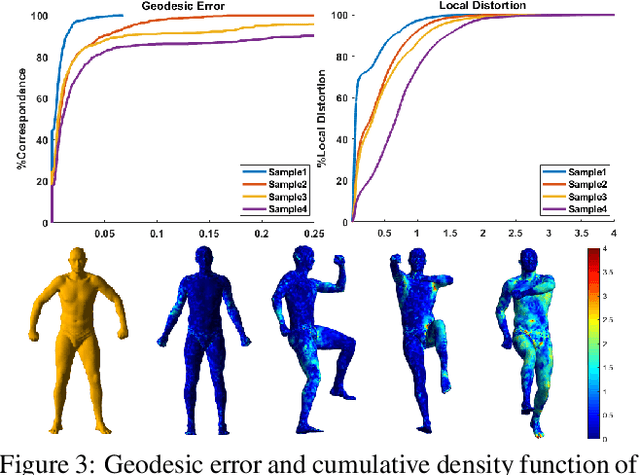
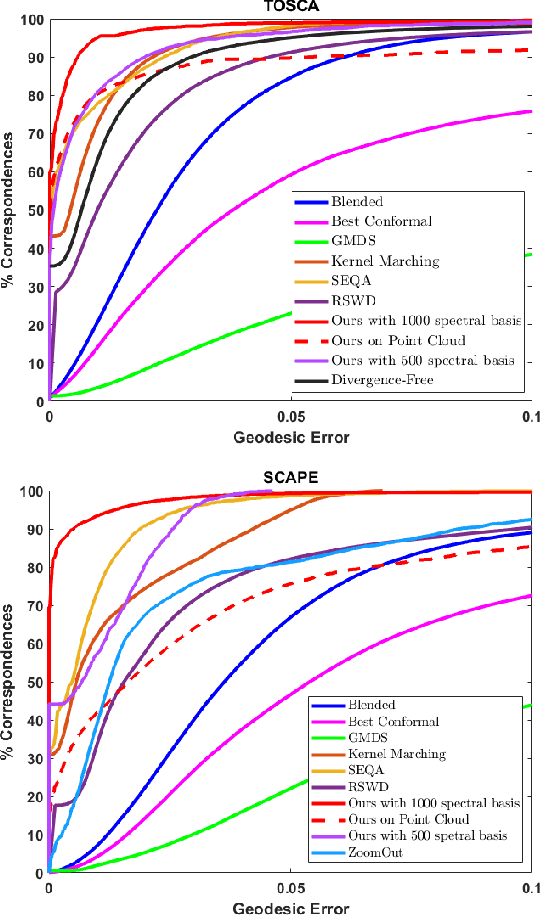
Efficient and Robust Shape Correspondence via Sparsity-Enforced Quadratic Assignment

In this work, we introduce a novel local pairwise descriptor and then develop a simple, effective iterative method to solve the resulting quadratic assignment through sparsity control for shape correspondence between two approximate isometric surfaces. Our pairwise descriptor is based on the stiffness and mass matrix of finite element approximation of the Laplace-Beltrami differential operator, which is local in space, sparse to represent, and extremely easy to compute while containing global information. It allows us to deal with open surfaces, partial matching, and topological perturbations robustly. To solve the resulting quadratic assignment problem efficiently, the two key ideas of our iterative algorithm are: 1) select pairs with good (approximate) correspondence as anchor points, 2) solve a regularized quadratic assignment problem only in the neighborhood of selected anchor points through sparsity control. These two ingredients can improve and increase the number of anchor points quickly while reducing the computation cost in each quadratic assignment iteration significantly. With enough high-quality anchor points, one may use various pointwise global features with reference to these anchor points to further improve the dense shape correspondence. We use various experiments to show the efficiency, quality, and versatility of our method on large data sets, patches, and point clouds (without global meshes).

A data-driven approach for multiscale elliptic PDEs with random coefficients based on intrinsic dimension reduction

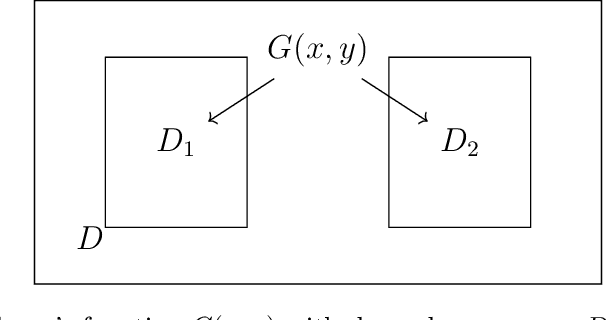
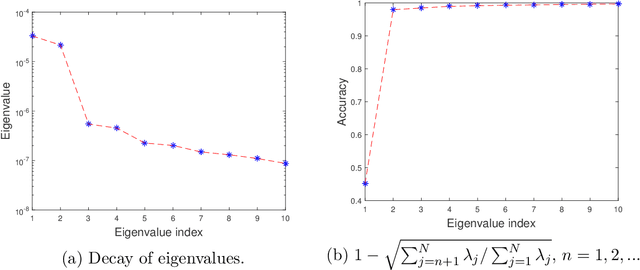
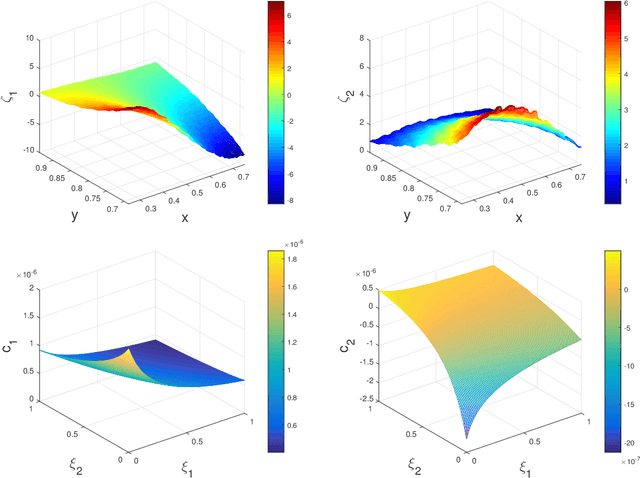
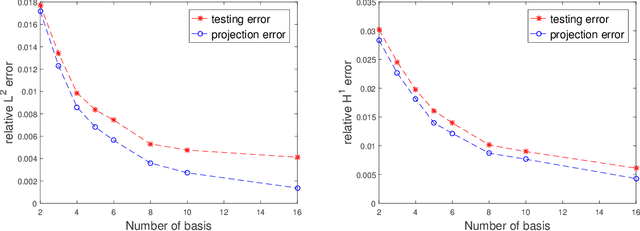
We propose a data-driven approach to solve multiscale elliptic PDEs with random coefficients based on the intrinsic low dimension structure of the underlying elliptic differential operators. Our method consists of offline and online stages. At the offline stage, a low dimension space and its basis are extracted from the data to achieve significant dimension reduction in the solution space. At the online stage, the extracted basis will be used to solve a new multiscale elliptic PDE efficiently. The existence of low dimension structure is established by showing the high separability of the underlying Green's functions. Different online construction methods are proposed depending on the problem setup. We provide error analysis based on the sampling error and the truncation threshold in building the data-driven basis. Finally, we present numerical examples to demonstrate the accuracy and efficiency of the proposed method.

Variational Hamiltonian Monte Carlo via Score Matching

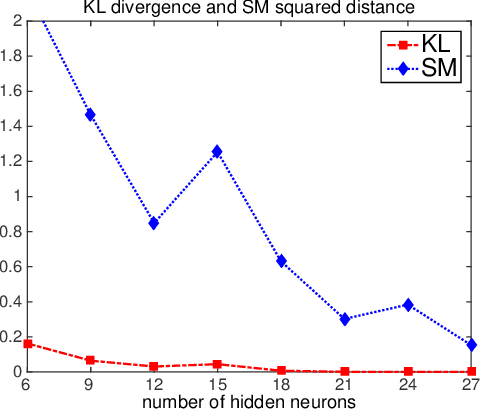
Traditionally, the field of computational Bayesian statistics has been divided into two main subfields: variational methods and Markov chain Monte Carlo (MCMC). In recent years, however, several methods have been proposed based on combining variational Bayesian inference and MCMC simulation in order to improve their overall accuracy and computational efficiency. This marriage of fast evaluation and flexible approximation provides a promising means of designing scalable Bayesian inference methods. In this paper, we explore the possibility of incorporating variational approximation into a state-of-the-art MCMC method, Hamiltonian Monte Carlo (HMC), to reduce the required gradient computation in the simulation of Hamiltonian flow, which is the bottleneck for many applications of HMC in big data problems. To this end, we use a {\it free-form} approximation induced by a fast and flexible surrogate function based on single-hidden layer feedforward neural networks. The surrogate provides sufficiently accurate approximation while allowing for fast exploration of parameter space, resulting in an efficient approximate inference algorithm. We demonstrate the advantages of our method on both synthetic and real data problems.

Hamiltonian Monte Carlo Acceleration Using Surrogate Functions with Random Bases

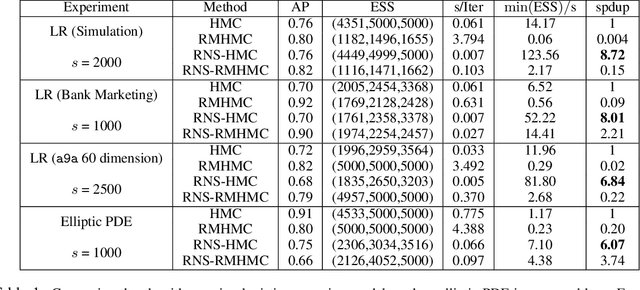
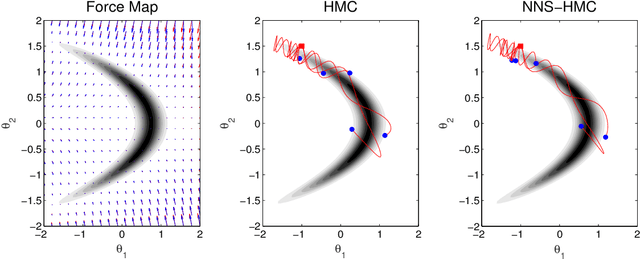
For big data analysis, high computational cost for Bayesian methods often limits their applications in practice. In recent years, there have been many attempts to improve computational efficiency of Bayesian inference. Here we propose an efficient and scalable computational technique for a state-of-the-art Markov Chain Monte Carlo (MCMC) methods, namely, Hamiltonian Monte Carlo (HMC). The key idea is to explore and exploit the structure and regularity in parameter space for the underlying probabilistic model to construct an effective approximation of its geometric properties. To this end, we build a surrogate function to approximate the target distribution using properly chosen random bases and an efficient optimization process. The resulting method provides a flexible, scalable, and efficient sampling algorithm, which converges to the correct target distribution. We show that by choosing the basis functions and optimization process differently, our method can be related to other approaches for the construction of surrogate functions such as generalized additive models or Gaussian process models. Experiments based on simulated and real data show that our approach leads to substantially more efficient sampling algorithms compared to existing state-of-the art methods.