Hyper-Compression: Model Compression via Hyperfunction

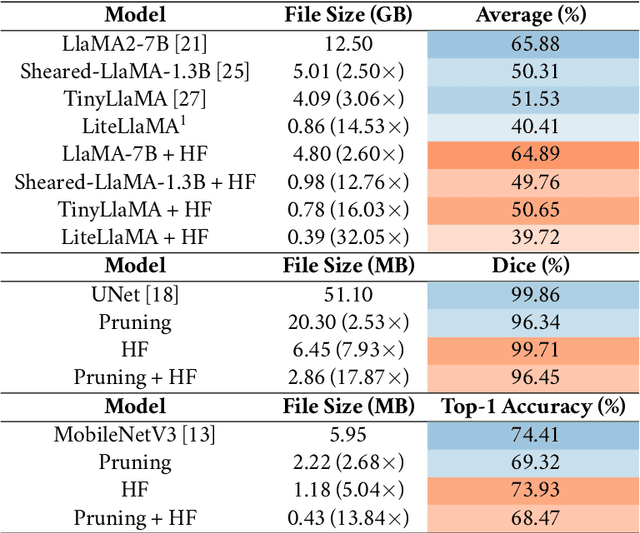
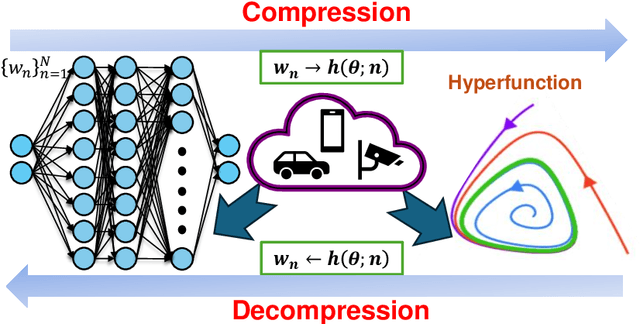
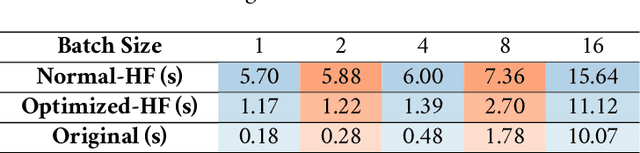
The rapid growth of large models' size has far outpaced that of GPU memory. To bridge this gap, inspired by the succinct relationship between genotype and phenotype, we turn the model compression problem into the issue of parameter representation to propose the so-called hyper-compression. The hyper-compression uses a hyperfunction to represent the parameters of the target network, and notably, here the hyperfunction is designed per ergodic theory that relates to a problem: if a low-dimensional dynamic system can fill the high-dimensional space eventually. Empirically, the proposed hyper-compression enjoys the following merits: 1) \textbf{P}referable compression ratio; 2) \textbf{N}o post-hoc retraining; 3) \textbf{A}ffordable inference time; and 4) \textbf{S}hort compression time. It compresses LLaMA2-7B in an hour and achieves close-to-int4-quantization performance, without retraining and with a performance drop of less than 1\%. Our work has the potential to invigorate the field of model compression, towards a harmony between the scaling law and the stagnation of hardware upgradation.

Don't Fear Peculiar Activation Functions: EUAF and Beyond

In this paper, we propose a new super-expressive activation function called the Parametric Elementary Universal Activation Function (PEUAF). We demonstrate the effectiveness of PEUAF through systematic and comprehensive experiments on various industrial and image datasets, including CIFAR10, Tiny-ImageNet, and ImageNet. Moreover, we significantly generalize the family of super-expressive activation functions, whose existence has been demonstrated in several recent works by showing that any continuous function can be approximated to any desired accuracy by a fixed-size network with a specific super-expressive activation function. Specifically, our work addresses two major bottlenecks in impeding the development of super-expressive activation functions: the limited identification of super-expressive functions, which raises doubts about their broad applicability, and their often peculiar forms, which lead to skepticism regarding their scalability and practicality in real-world applications.

Structured and Balanced Multi-component and Multi-layer Neural Networks

In this work, we propose a balanced multi-component and multi-layer neural network (MMNN) structure to approximate functions with complex features with both accuracy and efficiency in terms of degrees of freedom and computation cost. The main idea is motivated by a multi-component, each of which can be approximated effectively by a single-layer network, and multi-layer decomposition in a "divide-and-conquer" type of strategy to deal with a complex function. While an easy modification to fully connected neural networks (FCNNs) or multi-layer perceptrons (MLPs) through the introduction of balanced multi-component structures in the network, MMNNs achieve a significant reduction of training parameters, a much more efficient training process, and a much improved accuracy compared to FCNNs or MLPs. Extensive numerical experiments are presented to illustrate the effectiveness of MMNNs in approximating high oscillatory functions and its automatic adaptivity in capturing localized features.

Deep Network Approximation: Beyond ReLU to Diverse Activation Functions

This paper explores the expressive power of deep neural networks for a diverse range of activation functions. An activation function set $\mathscr{A}$ is defined to encompass the majority of commonly used activation functions, such as $\mathtt{ReLU}$, $\mathtt{LeakyReLU}$, $\mathtt{ReLU}^2$, $\mathtt{ELU}$, $\mathtt{SELU}$, $\mathtt{Softplus}$, $\mathtt{GELU}$, $\mathtt{SiLU}$, $\mathtt{Swish}$, $\mathtt{Mish}$, $\mathtt{Sigmoid}$, $\mathtt{Tanh}$, $\mathtt{Arctan}$, $\mathtt{Softsign}$, $\mathtt{dSiLU}$, and $\mathtt{SRS}$. We demonstrate that for any activation function $\varrho\in \mathscr{A}$, a $\mathtt{ReLU}$ network of width $N$ and depth $L$ can be approximated to arbitrary precision by a $\varrho$-activated network of width $6N$ and depth $2L$ on any bounded set. This finding enables the extension of most approximation results achieved with $\mathtt{ReLU}$ networks to a wide variety of other activation functions, at the cost of slightly larger constants.

Why Shallow Networks Struggle with Approximating and Learning High Frequency: A Numerical Study

In this work, a comprehensive numerical study involving analysis and experiments shows why a two-layer neural network has difficulties handling high frequencies in approximation and learning when machine precision and computation cost are important factors in real practice. In particular, the following fundamental computational issues are investigated: (1) the best accuracy one can achieve given a finite machine precision, (2) the computation cost to achieve a given accuracy, and (3) stability with respect to perturbations. The key to the study is the spectral analysis of the corresponding Gram matrix of the activation functions which also shows how the properties of the activation function play a role in the picture.

On Enhancing Expressive Power via Compositions of Single Fixed-Size ReLU Network

This paper studies the expressive power of deep neural networks from the perspective of function compositions. We show that repeated compositions of a single fixed-size ReLU network can produce super expressive power. In particular, we prove by construction that $\mathcal{L}_2\circ \boldsymbol{g}^{\circ r}\circ \boldsymbol{\mathcal{L}}_1$ can approximate $1$-Lipschitz continuous functions on $[0,1]^d$ with an error $\mathcal{O}(r^{-1/d})$, where $\boldsymbol{g}$ is realized by a fixed-size ReLU network, $\boldsymbol{\mathcal{L}}_1$ and $\mathcal{L}_2$ are two affine linear maps matching the dimensions, and $\boldsymbol{g}^{\circ r}$ means the $r$-times composition of $\boldsymbol{g}$. Furthermore, we extend such a result to generic continuous functions on $[0,1]^d$ with the approximation error characterized by the modulus of continuity. Our results reveal that a continuous-depth network generated via a dynamical system has good approximation power even if its dynamics function is time-independent and realized by a fixed-size ReLU network.

Neural Network Architecture Beyond Width and Depth

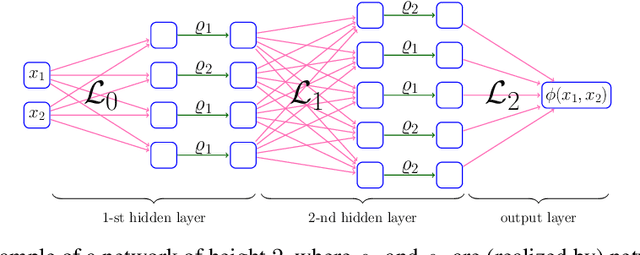
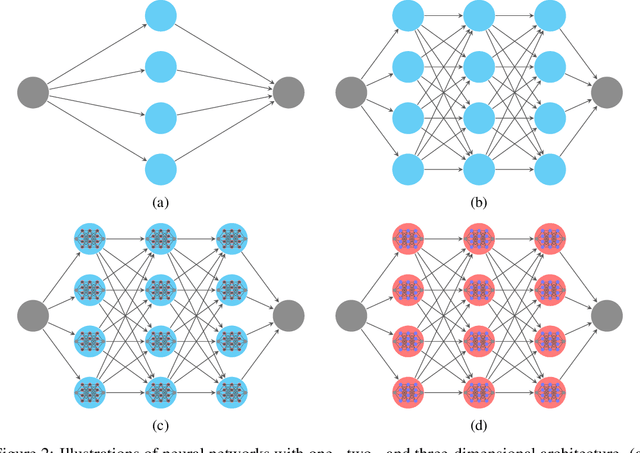
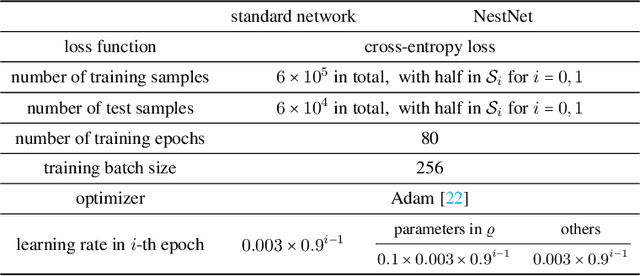
This paper proposes a new neural network architecture by introducing an additional dimension called height beyond width and depth. Neural network architectures with height, width, and depth as hyperparameters are called three-dimensional architectures. It is shown that neural networks with three-dimensional architectures are significantly more expressive than the ones with two-dimensional architectures (those with only width and depth as hyperparameters), e.g., standard fully connected networks. The new network architecture is constructed recursively via a nested structure, and hence we call a network with the new architecture nested network (NestNet). A NestNet of height $s$ is built with each hidden neuron activated by a NestNet of height $\le s-1$. When $s=1$, a NestNet degenerates to a standard network with a two-dimensional architecture. It is proved by construction that height-$s$ ReLU NestNets with $\mathcal{O}(n)$ parameters can approximate Lipschitz continuous functions on $[0,1]^d$ with an error $\mathcal{O}(n^{-(s+1)/d})$, while the optimal approximation error of standard ReLU networks with $\mathcal{O}(n)$ parameters is $\mathcal{O}(n^{-2/d})$. Furthermore, such a result is extended to generic continuous functions on $[0,1]^d$ with the approximation error characterized by the modulus of continuity. Finally, a numerical example is provided to explore the advantages of the super approximation power of ReLU NestNets.

ReLU Network Approximation in Terms of Intrinsic Parameters

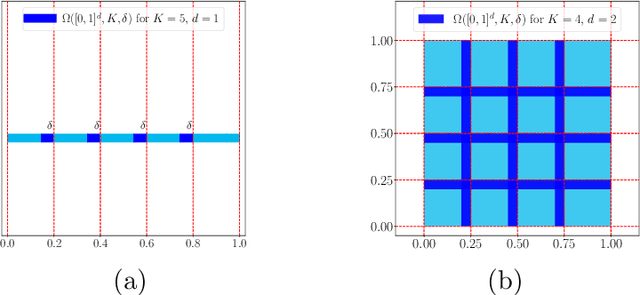
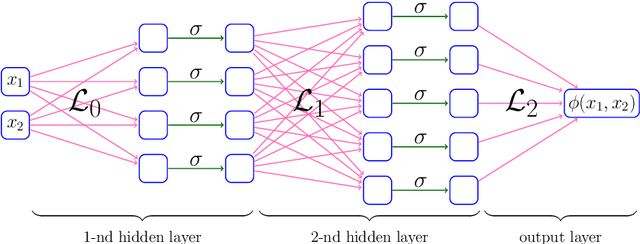
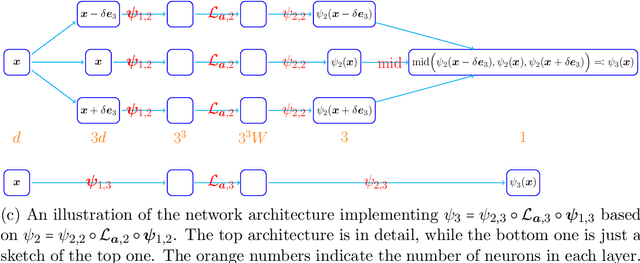
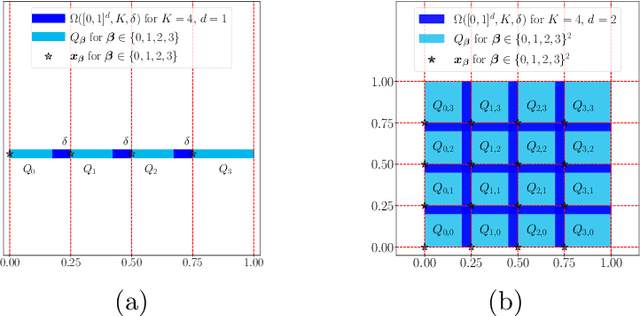
This paper studies the approximation error of ReLU networks in terms of the number of intrinsic parameters (i.e., those depending on the target function $f$). First, we prove by construction that, for any Lipschitz continuous function $f$ on $[0,1]^d$ with a Lipschitz constant $\lambda>0$, a ReLU network with $n+2$ intrinsic parameters can approximate $f$ with an exponentially small error $5\lambda \sqrt{d}\,2^{-n}$ measured in the $L^p$-norm for $p\in [1,\infty)$. More generally for an arbitrary continuous function $f$ on $[0,1]^d$ with a modulus of continuity $\omega_f(\cdot)$, the approximation error is $\omega_f(\sqrt{d}\, 2^{-n})+2^{-n+2}\omega_f(\sqrt{d})$. Next, we extend these two results from the $L^p$-norm to the $L^\infty$-norm at a price of $3^d n+2$ intrinsic parameters. Finally, by using a high-precision binary representation and the bit extraction technique via a fixed ReLU network independent of the target function, we design, theoretically, a ReLU network with only three intrinsic parameters to approximate H\"older continuous functions with an arbitrarily small error.

Deep Network Approximation: Achieving Arbitrary Accuracy with Fixed Number of Neurons

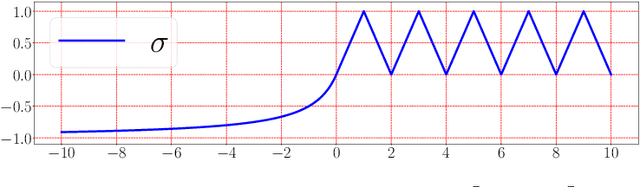
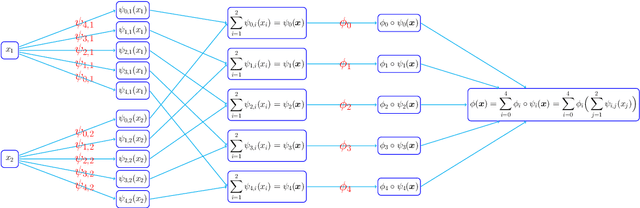
This paper develops simple feed-forward neural networks that achieve the universal approximation property for all continuous functions with a fixed finite number of neurons. These neural networks are simple because they are designed with a simple and computable continuous activation function $\sigma$ leveraging a triangular-wave function and a softsign function. We prove that $\sigma$-activated networks with width $36d(2d+1)$ and depth $11$ can approximate any continuous function on a $d$-dimensioanl hypercube within an arbitrarily small error. Hence, for supervised learning and its related regression problems, the hypothesis space generated by these networks with a size not smaller than $36d(2d+1)\times 11$ is dense in the space of continuous functions. Furthermore, classification functions arising from image and signal classification are in the hypothesis space generated by $\sigma$-activated networks with width $36d(2d+1)$ and depth $12$, when there exist pairwise disjoint closed bounded subsets of $\mathbb{R}^d$ such that the samples of the same class are located in the same subset.

Optimal Approximation Rate of ReLU Networks in terms of Width and Depth

This paper concentrates on the approximation power of deep feed-forward neural networks in terms of width and depth. It is proved by construction that ReLU networks with width $\mathcal{O}\big(\max\{d\lfloor N^{1/d}\rfloor,\, N+2\}\big)$ and depth $\mathcal{O}(L)$ can approximate a H\"older continuous function on $[0,1]^d$ with an approximation rate $\mathcal{O}\big(\lambda\sqrt{d} (N^2L^2\ln N)^{-\alpha/d}\big)$, where $\alpha\in (0,1]$ and $\lambda>0$ are H\"older order and constant, respectively. Such a rate is optimal up to a constant in terms of width and depth separately, while existing results are only nearly optimal without the logarithmic factor in the approximation rate. More generally, for an arbitrary continuous function $f$ on $[0,1]^d$, the approximation rate becomes $\mathcal{O}\big(\,\sqrt{d}\,\omega_f\big( (N^2L^2\ln N)^{-1/d}\big)\,\big)$, where $\omega_f(\cdot)$ is the modulus of continuity. We also extend our analysis to any continuous function $f$ on a bounded set. Particularly, if ReLU networks with depth $31$ and width $\mathcal{O}(N)$ are used to approximate one-dimensional Lipschitz continuous functions on $[0,1]$ with a Lipschitz constant $\lambda>0$, the approximation rate in terms of the total number of parameters, $W=\mathcal{O}(N^2)$, becomes $\mathcal{O}(\tfrac{\lambda}{W\ln W})$, which has not been discovered in the literature for fixed-depth ReLU networks.