Retinal Vessel Segmentation via Neuron Programming

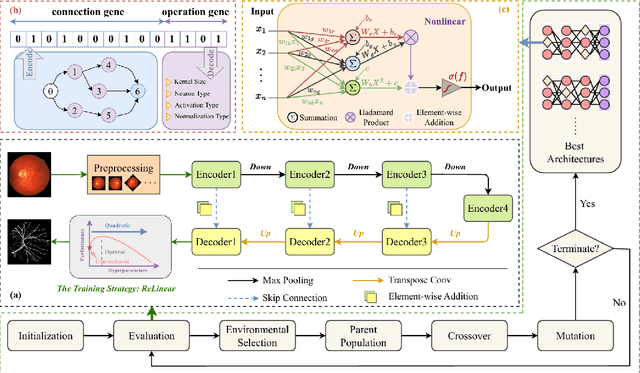
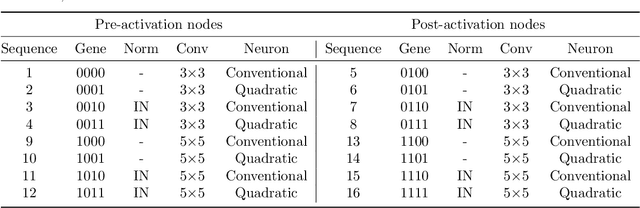
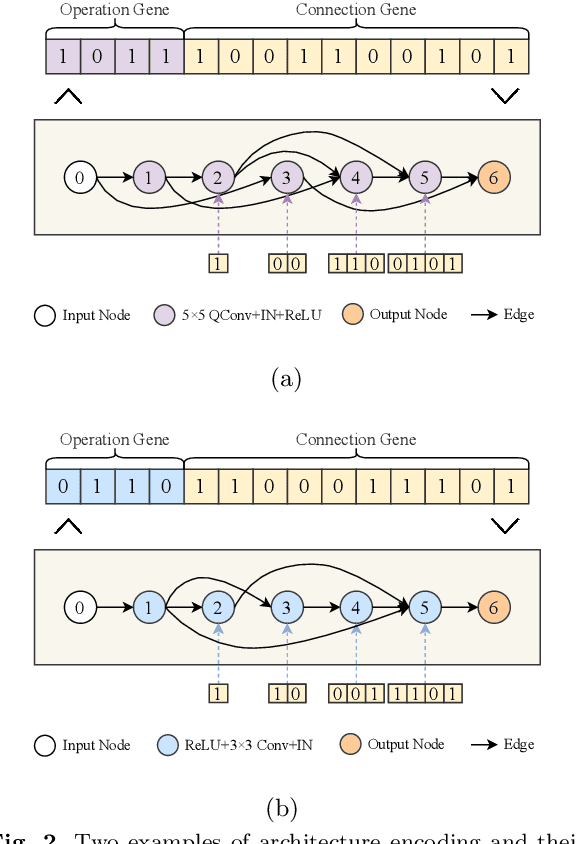
The accurate segmentation of retinal blood vessels plays a crucial role in the early diagnosis and treatment of various ophthalmic diseases. Designing a network model for this task requires meticulous tuning and extensive experimentation to handle the tiny and intertwined morphology of retinal blood vessels. To tackle this challenge, Neural Architecture Search (NAS) methods are developed to fully explore the space of potential network architectures and go after the most powerful one. Inspired by neuronal diversity which is the biological foundation of all kinds of intelligent behaviors in our brain, this paper introduces a novel and foundational approach to neural network design, termed ``neuron programming'', to automatically search neuronal types into a network to enhance a network's representation ability at the neuronal level, which is complementary to architecture-level enhancement done by NAS. Additionally, to mitigate the time and computational intensity of neuron programming, we develop a hypernetwork that leverages the search-derived architectural information to predict optimal neuronal configurations. Comprehensive experiments validate that neuron programming can achieve competitive performance in retinal blood segmentation, demonstrating the strong potential of neuronal diversity in medical image analysis.

Don't Fear Peculiar Activation Functions: EUAF and Beyond

In this paper, we propose a new super-expressive activation function called the Parametric Elementary Universal Activation Function (PEUAF). We demonstrate the effectiveness of PEUAF through systematic and comprehensive experiments on various industrial and image datasets, including CIFAR10, Tiny-ImageNet, and ImageNet. Moreover, we significantly generalize the family of super-expressive activation functions, whose existence has been demonstrated in several recent works by showing that any continuous function can be approximated to any desired accuracy by a fixed-size network with a specific super-expressive activation function. Specifically, our work addresses two major bottlenecks in impeding the development of super-expressive activation functions: the limited identification of super-expressive functions, which raises doubts about their broad applicability, and their often peculiar forms, which lead to skepticism regarding their scalability and practicality in real-world applications.

No One-Size-Fits-All Neurons: Task-based Neurons for Artificial Neural Networks

Biologically, the brain does not rely on a single type of neuron that universally functions in all aspects. Instead, it acts as a sophisticated designer of task-based neurons. In this study, we address the following question: since the human brain is a task-based neuron user, can the artificial network design go from the task-based architecture design to the task-based neuron design? Since methodologically there are no one-size-fits-all neurons, given the same structure, task-based neurons can enhance the feature representation ability relative to the existing universal neurons due to the intrinsic inductive bias for the task. Specifically, we propose a two-step framework for prototyping task-based neurons. First, symbolic regression is used to identify optimal formulas that fit input data by utilizing base functions such as logarithmic, trigonometric, and exponential functions. We introduce vectorized symbolic regression that stacks all variables in a vector and regularizes each input variable to perform the same computation, which can expedite the regression speed, facilitate parallel computation, and avoid overfitting. Second, we parameterize the acquired elementary formula to make parameters learnable, which serves as the aggregation function of the neuron. The activation functions such as ReLU and the sigmoidal functions remain the same because they have proven to be good. Empirically, experimental results on synthetic data, classic benchmarks, and real-world applications show that the proposed task-based neuron design is not only feasible but also delivers competitive performance over other state-of-the-art models.

EEG-DG: A Multi-Source Domain Generalization Framework for Motor Imagery EEG Classification

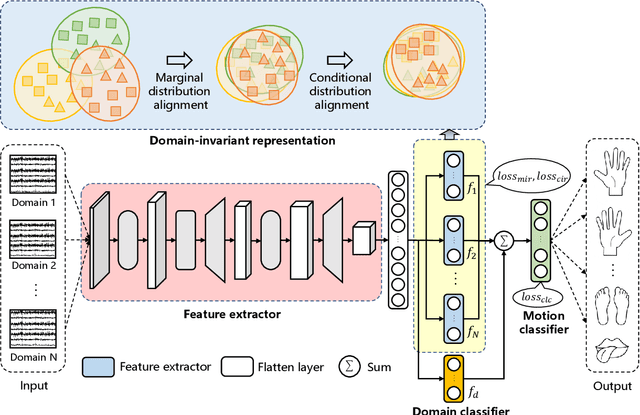
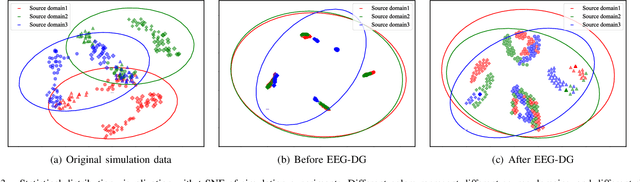
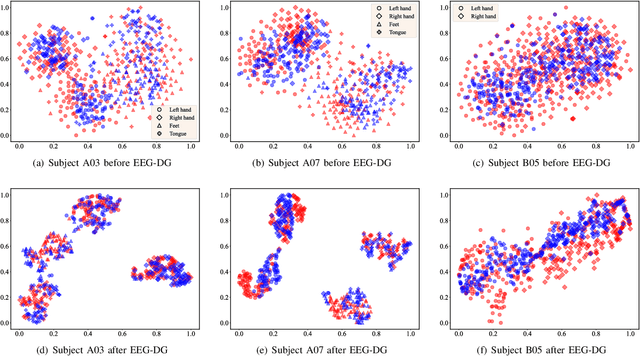
Motor imagery EEG classification plays a crucial role in non-invasive Brain-Computer Interface (BCI) research. However, the classification is affected by the non-stationarity and individual variations of EEG signals. Simply pooling EEG data with different statistical distributions to train a classification model can severely degrade the generalization performance. To address this issue, the existing methods primarily focus on domain adaptation, which requires access to the target data during training. This is unrealistic in many EEG application scenarios. In this paper, we propose a novel multi-source domain generalization framework called EEG-DG, which leverages multiple source domains with different statistical distributions to build generalizable models on unseen target EEG data. We optimize both the marginal and conditional distributions to ensure the stability of the joint distribution across source domains and extend it to a multi-source domain generalization framework to achieve domain-invariant feature representation, thereby alleviating calibration efforts. Systematic experiments on a simulative dataset and BCI competition datasets IV-2a and IV-2b demonstrate the superiority of our proposed EEG-DG over state-of-the-art methods. Specifically, EEG-DG achieves an average classification accuracy/kappa value of 81.79%/0.7572 and 87.12%/0.7424 on datasets IV-2a and IV-2b, respectively, which even outperforms some domain adaptation methods. Our code is available at https://github.com/XC-ZhongHIT/EEG-DG for free download and evaluation.

VDIP-TGV: Blind Image Deconvolution via Variational Deep Image Prior Empowered by Total Generalized Variation

Recovering clear images from blurry ones with an unknown blur kernel is a challenging problem. Deep image prior (DIP) proposes to use the deep network as a regularizer for a single image rather than as a supervised model, which achieves encouraging results in the nonblind deblurring problem. However, since the relationship between images and the network architectures is unclear, it is hard to find a suitable architecture to provide sufficient constraints on the estimated blur kernels and clean images. Also, DIP uses the sparse maximum a posteriori (MAP), which is insufficient to enforce the selection of the recovery image. Recently, variational deep image prior (VDIP) was proposed to impose constraints on both blur kernels and recovery images and take the standard deviation of the image into account during the optimization process by the variational principle. However, we empirically find that VDIP struggles with processing image details and tends to generate suboptimal results when the blur kernel is large. Therefore, we combine total generalized variational (TGV) regularization with VDIP in this paper to overcome these shortcomings of VDIP. TGV is a flexible regularization that utilizes the characteristics of partial derivatives of varying orders to regularize images at different scales, reducing oil painting artifacts while maintaining sharp edges. The proposed VDIP-TGV effectively recovers image edges and details by supplementing extra gradient information through TGV. Additionally, this model is solved by the alternating direction method of multipliers (ADMM), which effectively combines traditional algorithms and deep learning methods. Experiments show that our proposed VDIP-TGV surpasses various state-of-the-art models quantitatively and qualitatively.

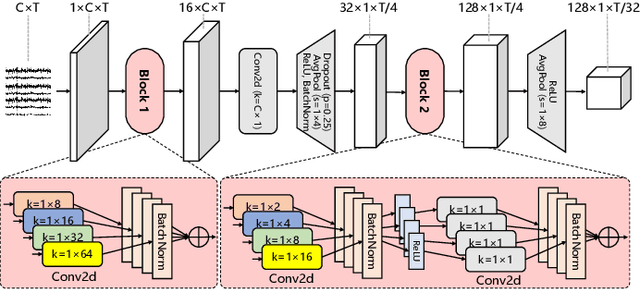
BearingPGA-Net: A Lightweight and Deployable Bearing Fault Diagnosis Network via Decoupled Knowledge Distillation and FPGA Acceleration

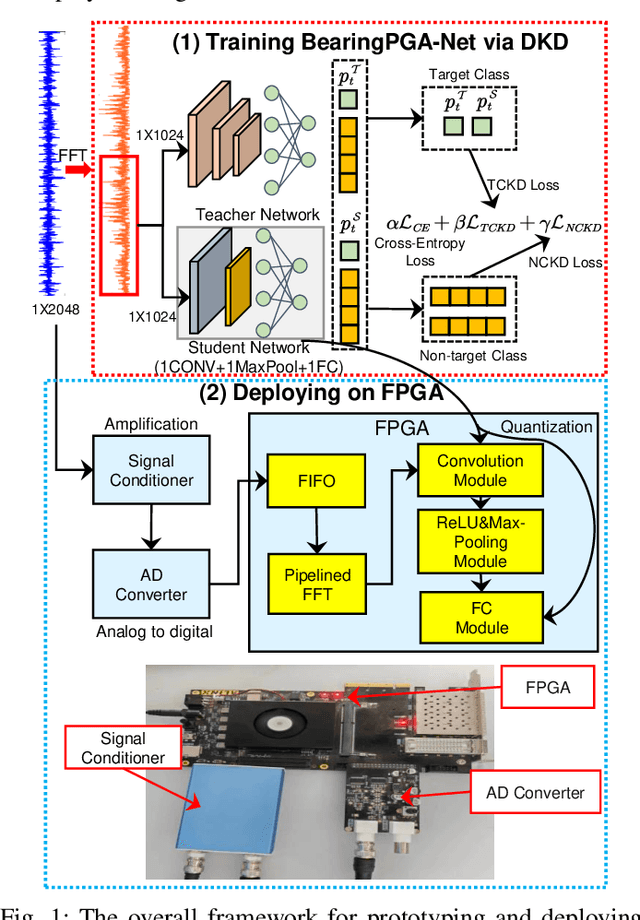
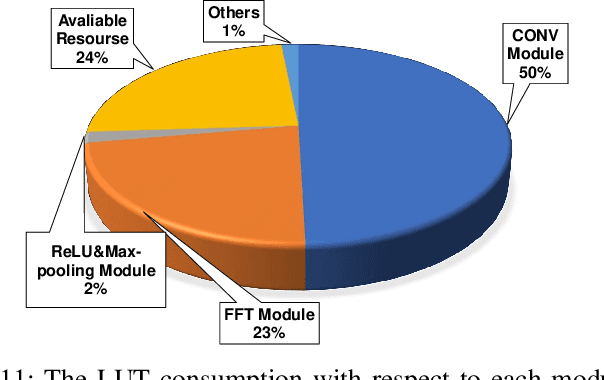
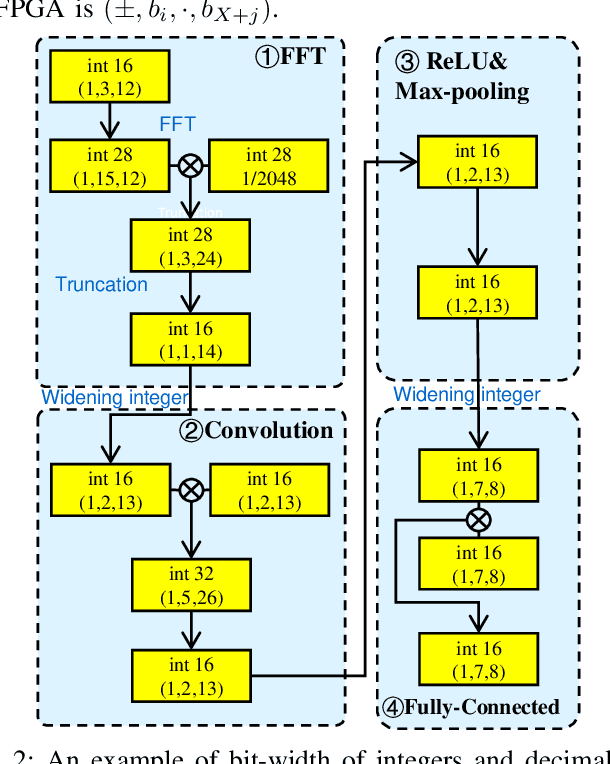
Deep learning has achieved remarkable success in the field of bearing fault diagnosis. However, this success comes with larger models and more complex computations, which cannot be transferred into industrial fields requiring models to be of high speed, strong portability, and low power consumption. In this paper, we propose a lightweight and deployable model for bearing fault diagnosis, referred to as BearingPGA-Net, to address these challenges. Firstly, aided by a well-trained large model, we train BearingPGA-Net via decoupled knowledge distillation. Despite its small size, our model demonstrates excellent fault diagnosis performance compared to other lightweight state-of-the-art methods. Secondly, we design an FPGA acceleration scheme for BearingPGA-Net using Verilog. This scheme involves the customized quantization and designing programmable logic gates for each layer of BearingPGA-Net on the FPGA, with an emphasis on parallel computing and module reuse to enhance the computational speed. To the best of our knowledge, this is the first instance of deploying a CNN-based bearing fault diagnosis model on an FPGA. Experimental results reveal that our deployment scheme achieves over 200 times faster diagnosis speed compared to CPU, while achieving a lower-than-0.4\% performance drop in terms of F1, Recall, and Precision score on our independently-collected bearing dataset. Our code is available at \url{https://github.com/asdvfghg/BearingPGA-Net}.

Deep ReLU Networks Have Surprisingly Simple Polytopes

A ReLU network is a piecewise linear function over polytopes. Figuring out the properties of such polytopes is of fundamental importance for the research and development of neural networks. So far, either theoretical or empirical studies on polytopes only stay at the level of counting their number, which is far from a complete characterization of polytopes. To upgrade the characterization to a new level, here we propose to study the shapes of polytopes via the number of simplices obtained by triangulating the polytope. Then, by computing and analyzing the histogram of simplices across polytopes, we find that a ReLU network has relatively simple polytopes under both initialization and gradient descent, although these polytopes theoretically can be rather diverse and complicated. This finding can be appreciated as a novel implicit bias. Next, we use nontrivial combinatorial derivation to theoretically explain why adding depth does not create a more complicated polytope by bounding the average number of faces of polytopes with a function of the dimensionality. Our results concretely reveal what kind of simple functions a network learns and its space partition property. Also, by characterizing the shape of polytopes, the number of simplices be a leverage for other problems, \textit{e.g.}, serving as a generic functional complexity measure to explain the power of popular shortcut networks such as ResNet and analyzing the impact of different regularization strategies on a network's space partition.

Cloud-RAIN: Point Cloud Analysis with Reflectional Invariance

The networks for point cloud tasks are expected to be invariant when the point clouds are affinely transformed such as rotation and reflection. So far, relative to the rotational invariance that has been attracting major research attention in the past years, the reflection invariance is little addressed. Notwithstanding, reflection symmetry can find itself in very common and important scenarios, e.g., static reflection symmetry of structured streets, dynamic reflection symmetry from bidirectional motion of moving objects (such as pedestrians), and left- and right-hand traffic practices in different countries. To the best of our knowledge, unfortunately, no reflection-invariant network has been reported in point cloud analysis till now. To fill this gap, we propose a framework by using quadratic neurons and PCA canonical representation, referred to as Cloud-RAIN, to endow point \underline{Cloud} models with \underline{R}eflection\underline{A}l \underline{IN}variance. We prove a theorem to explain why Cloud-RAIN can enjoy reflection symmetry. Furthermore, extensive experiments also corroborate the reflection property of the proposed Cloud-RAIN and show that Cloud-RAIN is superior to data augmentation. Our code is available at https://github.com/YimingCuiCuiCui/Cloud-RAIN.

Rethink Depth Separation with Intra-layer Links

The depth separation theory is nowadays widely accepted as an effective explanation for the power of depth, which consists of two parts: i) there exists a function representable by a deep network; ii) such a function cannot be represented by a shallow network whose width is lower than a threshold. However, this theory is established for feedforward networks. Few studies, if not none, considered the depth separation theory in the context of shortcuts which are the most common network types in solving real-world problems. Here, we find that adding intra-layer links can modify the depth separation theory. First, we report that adding intra-layer links can greatly improve a network's representation capability through bound estimation, explicit construction, and functional space analysis. Then, we modify the depth separation theory by showing that a shallow network with intra-layer links does not need to go as wide as before to express some hard functions constructed by a deep network. Such functions include the renowned "sawtooth" functions. Moreover, the saving of width is up to linear. Our results supplement the existing depth separation theory by examining its limit in the shortcut domain. Also, the mechanism we identify can be translated into analyzing the expressivity of popular shortcut networks such as ResNet and DenseNet, \textit{e.g.}, residual connections empower a network to represent a sawtooth function efficiently.

One Neuron Saved Is One Neuron Earned: On Parametric Efficiency of Quadratic Networks

Inspired by neuronal diversity in the biological neural system, a plethora of studies proposed to design novel types of artificial neurons and introduce neuronal diversity into artificial neural networks. Recently proposed quadratic neuron, which replaces the inner-product operation in conventional neurons with a quadratic one, have achieved great success in many essential tasks. Despite the promising results of quadratic neurons, there is still an unresolved issue: \textit{Is the superior performance of quadratic networks simply due to the increased parameters or due to the intrinsic expressive capability?} Without clarifying this issue, the performance of quadratic networks is always suspicious. Additionally, resolving this issue is reduced to finding killer applications of quadratic networks. In this paper, with theoretical and empirical studies, we show that quadratic networks enjoy parametric efficiency, thereby confirming that the superior performance of quadratic networks is due to the intrinsic expressive capability. This intrinsic expressive ability comes from that quadratic neurons can easily represent nonlinear interaction, while it is hard for conventional neurons. Theoretically, we derive the approximation efficiency of the quadratic network over conventional ones in terms of real space and manifolds. Moreover, from the perspective of the Barron space, we demonstrate that there exists a functional space whose functions can be approximated by quadratic networks in a dimension-free error, but the approximation error of conventional networks is dependent on dimensions. Empirically, experimental results on synthetic data, classic benchmarks, and real-world applications show that quadratic models broadly enjoy parametric efficiency, and the gain of efficiency depends on the task.