EEG-DG: A Multi-Source Domain Generalization Framework for Motor Imagery EEG Classification

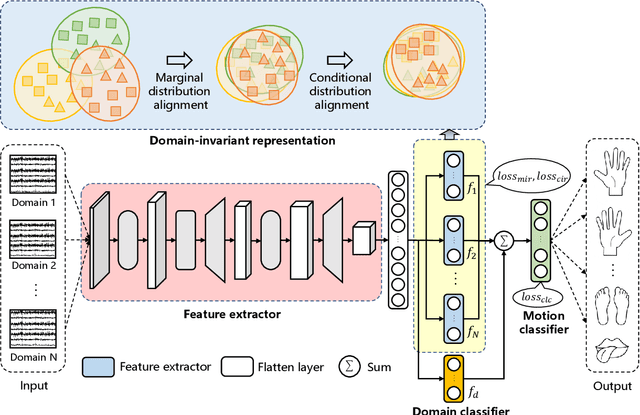
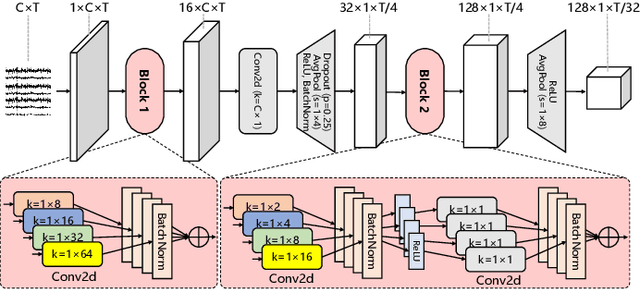
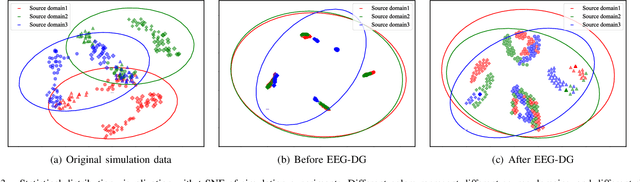
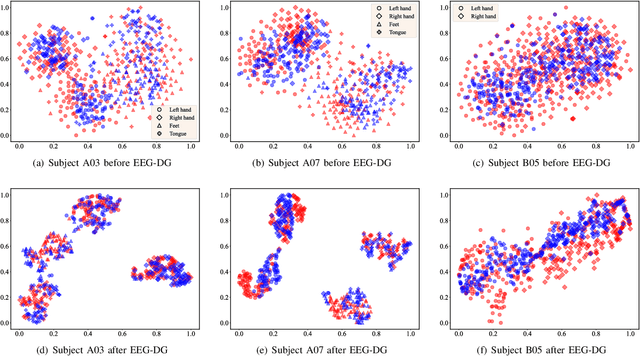
Motor imagery EEG classification plays a crucial role in non-invasive Brain-Computer Interface (BCI) research. However, the classification is affected by the non-stationarity and individual variations of EEG signals. Simply pooling EEG data with different statistical distributions to train a classification model can severely degrade the generalization performance. To address this issue, the existing methods primarily focus on domain adaptation, which requires access to the target data during training. This is unrealistic in many EEG application scenarios. In this paper, we propose a novel multi-source domain generalization framework called EEG-DG, which leverages multiple source domains with different statistical distributions to build generalizable models on unseen target EEG data. We optimize both the marginal and conditional distributions to ensure the stability of the joint distribution across source domains and extend it to a multi-source domain generalization framework to achieve domain-invariant feature representation, thereby alleviating calibration efforts. Systematic experiments on a simulative dataset and BCI competition datasets IV-2a and IV-2b demonstrate the superiority of our proposed EEG-DG over state-of-the-art methods. Specifically, EEG-DG achieves an average classification accuracy/kappa value of 81.79%/0.7572 and 87.12%/0.7424 on datasets IV-2a and IV-2b, respectively, which even outperforms some domain adaptation methods. Our code is available at https://github.com/XC-ZhongHIT/EEG-DG for free download and evaluation.

A class-weighted supervised contrastive learning long-tailed bearing fault diagnosis approach using quadratic neural network

Deep learning has achieved remarkable success in bearing fault diagnosis. However, its performance oftentimes deteriorates when dealing with highly imbalanced or long-tailed data, while such cases are prevalent in industrial settings because fault is a rare event that occurs with an extremely low probability. Conventional data augmentation methods face fundamental limitations due to the scarcity of samples pertaining to the minority class. In this paper, we propose a supervised contrastive learning approach with a class-aware loss function to enhance the feature extraction capability of neural networks for fault diagnosis. The developed class-weighted contrastive learning quadratic network (CCQNet) consists of a quadratic convolutional residual network backbone, a contrastive learning branch utilizing a class-weighted contrastive loss, and a classifier branch employing logit-adjusted cross-entropy loss. By utilizing class-weighted contrastive loss and logit-adjusted cross-entropy loss, our approach encourages equidistant representation of class features, thereby inducing equal attention on all the classes. We further analyze the superior feature extraction ability of quadratic network by establishing the connection between quadratic neurons and autocorrelation in signal processing. Experimental results on public and proprietary datasets are used to validate the effectiveness of CCQNet, and computational results reveal that CCQNet outperforms SOTA methods in handling extremely imbalanced data substantially.

BearingPGA-Net: A Lightweight and Deployable Bearing Fault Diagnosis Network via Decoupled Knowledge Distillation and FPGA Acceleration

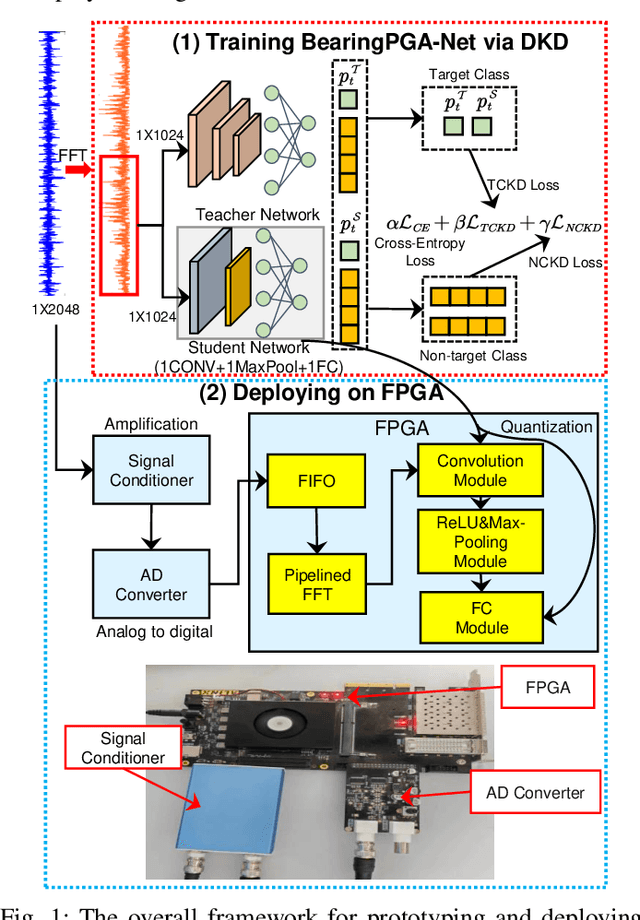
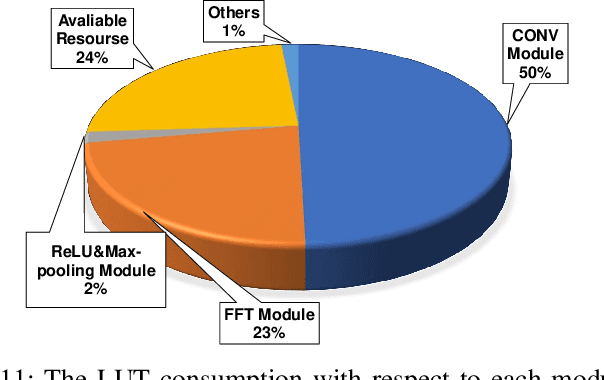
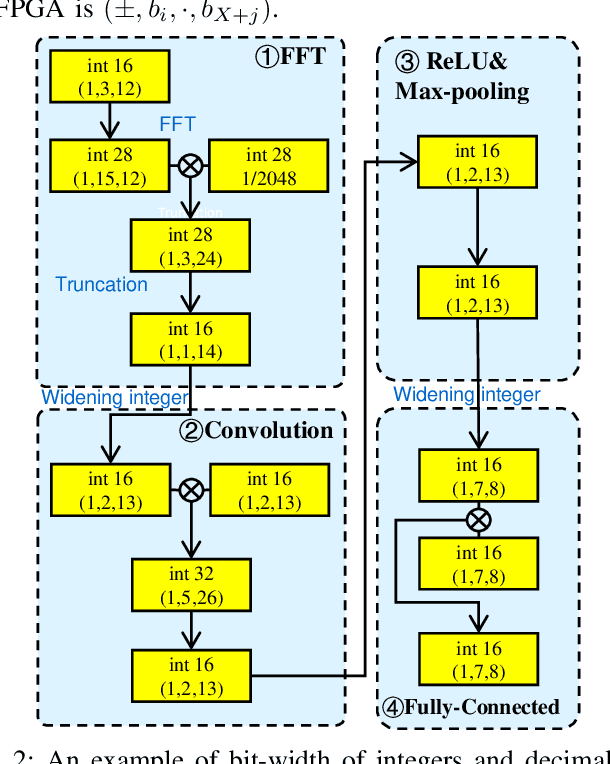
Deep learning has achieved remarkable success in the field of bearing fault diagnosis. However, this success comes with larger models and more complex computations, which cannot be transferred into industrial fields requiring models to be of high speed, strong portability, and low power consumption. In this paper, we propose a lightweight and deployable model for bearing fault diagnosis, referred to as BearingPGA-Net, to address these challenges. Firstly, aided by a well-trained large model, we train BearingPGA-Net via decoupled knowledge distillation. Despite its small size, our model demonstrates excellent fault diagnosis performance compared to other lightweight state-of-the-art methods. Secondly, we design an FPGA acceleration scheme for BearingPGA-Net using Verilog. This scheme involves the customized quantization and designing programmable logic gates for each layer of BearingPGA-Net on the FPGA, with an emphasis on parallel computing and module reuse to enhance the computational speed. To the best of our knowledge, this is the first instance of deploying a CNN-based bearing fault diagnosis model on an FPGA. Experimental results reveal that our deployment scheme achieves over 200 times faster diagnosis speed compared to CPU, while achieving a lower-than-0.4\% performance drop in terms of F1, Recall, and Precision score on our independently-collected bearing dataset. Our code is available at \url{https://github.com/asdvfghg/BearingPGA-Net}.

One Neuron Saved Is One Neuron Earned: On Parametric Efficiency of Quadratic Networks

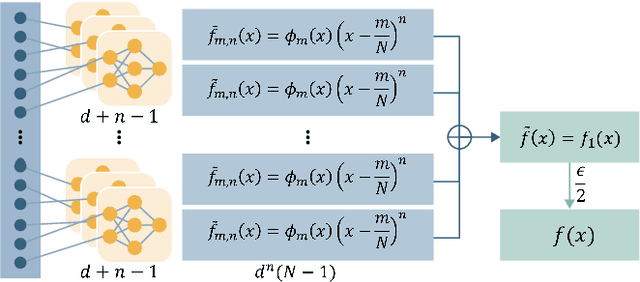
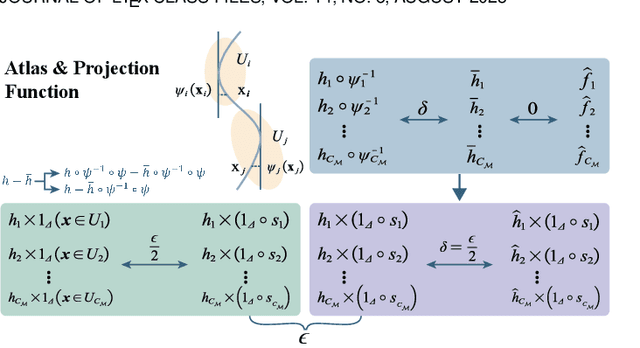
Inspired by neuronal diversity in the biological neural system, a plethora of studies proposed to design novel types of artificial neurons and introduce neuronal diversity into artificial neural networks. Recently proposed quadratic neuron, which replaces the inner-product operation in conventional neurons with a quadratic one, have achieved great success in many essential tasks. Despite the promising results of quadratic neurons, there is still an unresolved issue: \textit{Is the superior performance of quadratic networks simply due to the increased parameters or due to the intrinsic expressive capability?} Without clarifying this issue, the performance of quadratic networks is always suspicious. Additionally, resolving this issue is reduced to finding killer applications of quadratic networks. In this paper, with theoretical and empirical studies, we show that quadratic networks enjoy parametric efficiency, thereby confirming that the superior performance of quadratic networks is due to the intrinsic expressive capability. This intrinsic expressive ability comes from that quadratic neurons can easily represent nonlinear interaction, while it is hard for conventional neurons. Theoretically, we derive the approximation efficiency of the quadratic network over conventional ones in terms of real space and manifolds. Moreover, from the perspective of the Barron space, we demonstrate that there exists a functional space whose functions can be approximated by quadratic networks in a dimension-free error, but the approximation error of conventional networks is dependent on dimensions. Empirically, experimental results on synthetic data, classic benchmarks, and real-world applications show that quadratic models broadly enjoy parametric efficiency, and the gain of efficiency depends on the task.

Attention-embedded Quadratic Network (Qttention) for Effective and Interpretable Bearing Fault Diagnosis

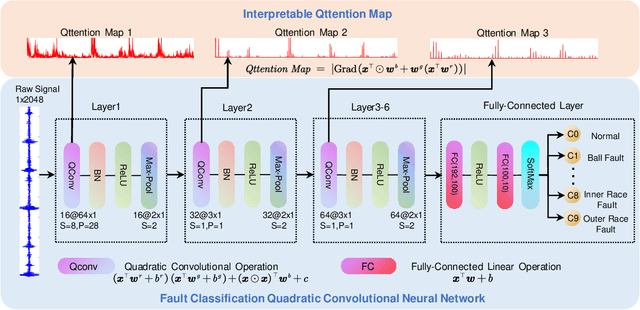
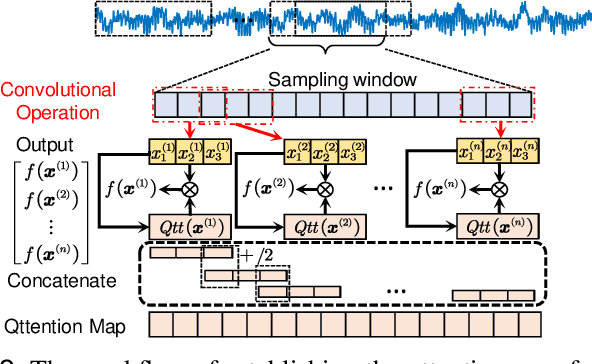
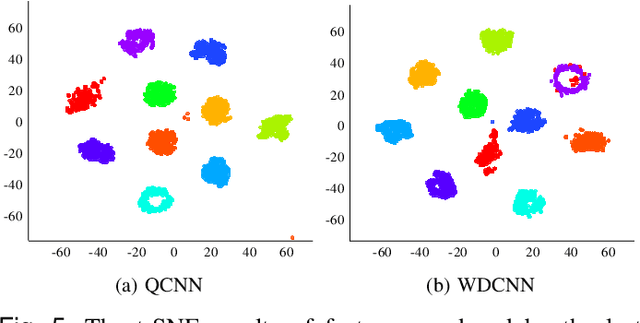
Bearing fault diagnosis is of great importance to decrease the damage risk of rotating machines and further improve economic profits. Recently, machine learning, represented by deep learning, has made great progress in bearing fault diagnosis. However, applying deep learning to such a task still faces two major problems. On the one hand, deep learning loses its effectiveness when bearing data are noisy or big data are unavailable, making deep learning hard to implement in industrial fields. On the other hand, a deep network is notoriously a black box. It is difficult to know how a model classifies faulty signals from the normal and the physics principle behind the classification. To solve the effectiveness and interpretability issues, we prototype a convolutional network with recently-invented quadratic neurons. This quadratic neuron empowered network can qualify the noisy and small bearing data due to the strong feature representation ability of quadratic neurons. Moreover, we independently derive the attention mechanism from a quadratic neuron, referred to as qttention, by factorizing the learned quadratic function in analogue to the attention, making the model with quadratic neurons inherently interpretable. Experiments on the public and our datasets demonstrate that the proposed network can facilitate effective and interpretable bearing fault diagnosis.

Heterogeneous Autoencoder Empowered by Quadratic Neurons

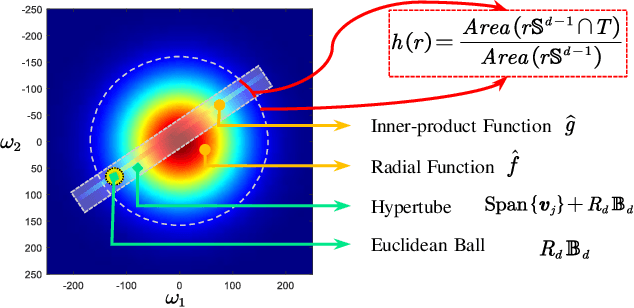
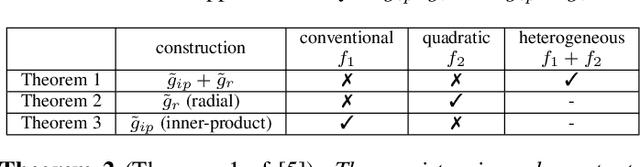
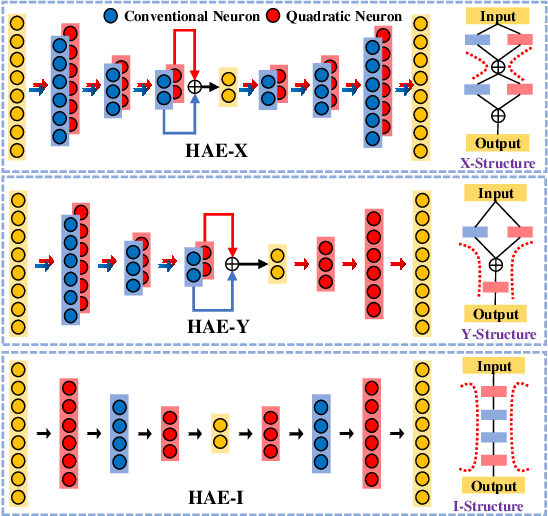
Inspired by the complexity and diversity of biological neurons, a quadratic neuron is proposed to replace the inner product in the current neuron with a simplified quadratic function. Employing such a novel type of neurons offers a new perspective on developing deep learning. When analyzing quadratic neurons, we find that there exists a function such that a heterogeneous network can approximate it well with a polynomial number of neurons but a purely conventional or quadratic network needs an exponential number of neurons to achieve the same level of error. Encouraged by this inspiring theoretical result on heterogeneous networks, we directly integrate conventional and quadratic neurons in an autoencoder to make a new type of heterogeneous autoencoders. Anomaly detection experiments confirm that heterogeneous autoencoders perform competitively compared to other state-of-the-art models.