Edge-guided Low-light Image Enhancement with Inertial Bregman Alternating Linearized Minimization

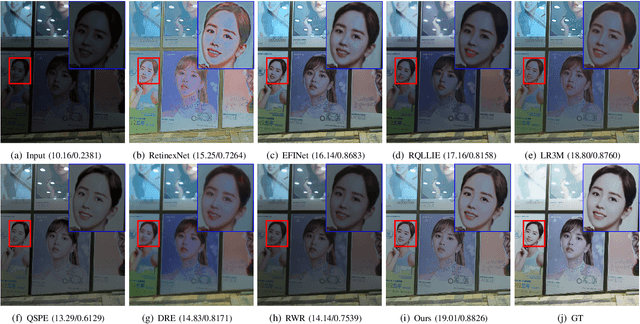
Prior-based methods for low-light image enhancement often face challenges in extracting available prior information from dim images. To overcome this limitation, we introduce a simple yet effective Retinex model with the proposed edge extraction prior. More specifically, we design an edge extraction network to capture the fine edge features from the low-light image directly. Building upon the Retinex theory, we decompose the low-light image into its illumination and reflectance components and introduce an edge-guided Retinex model for enhancing low-light images. To solve the proposed model, we propose a novel inertial Bregman alternating linearized minimization algorithm. This algorithm addresses the optimization problem associated with the edge-guided Retinex model, enabling effective enhancement of low-light images. Through rigorous theoretical analysis, we establish the convergence properties of the algorithm. Besides, we prove that the proposed algorithm converges to a stationary point of the problem through nonconvex optimization theory. Furthermore, extensive experiments are conducted on multiple real-world low-light image datasets to demonstrate the efficiency and superiority of the proposed scheme.

Cloud-RAIN: Point Cloud Analysis with Reflectional Invariance

The networks for point cloud tasks are expected to be invariant when the point clouds are affinely transformed such as rotation and reflection. So far, relative to the rotational invariance that has been attracting major research attention in the past years, the reflection invariance is little addressed. Notwithstanding, reflection symmetry can find itself in very common and important scenarios, e.g., static reflection symmetry of structured streets, dynamic reflection symmetry from bidirectional motion of moving objects (such as pedestrians), and left- and right-hand traffic practices in different countries. To the best of our knowledge, unfortunately, no reflection-invariant network has been reported in point cloud analysis till now. To fill this gap, we propose a framework by using quadratic neurons and PCA canonical representation, referred to as Cloud-RAIN, to endow point \underline{Cloud} models with \underline{R}eflection\underline{A}l \underline{IN}variance. We prove a theorem to explain why Cloud-RAIN can enjoy reflection symmetry. Furthermore, extensive experiments also corroborate the reflection property of the proposed Cloud-RAIN and show that Cloud-RAIN is superior to data augmentation. Our code is available at https://github.com/YimingCuiCuiCui/Cloud-RAIN.

One Neuron Saved Is One Neuron Earned: On Parametric Efficiency of Quadratic Networks

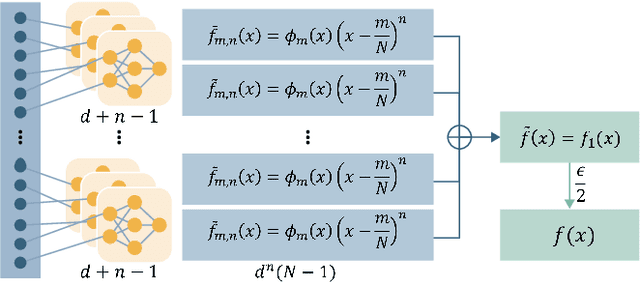
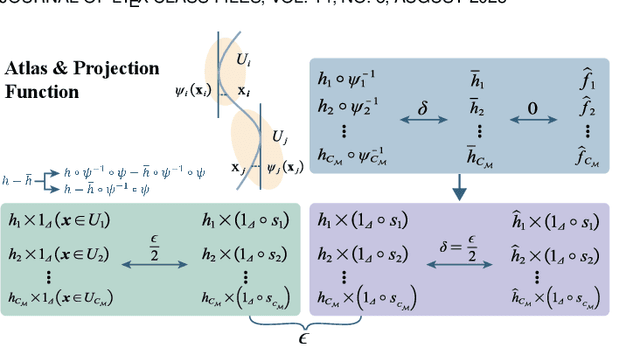
Inspired by neuronal diversity in the biological neural system, a plethora of studies proposed to design novel types of artificial neurons and introduce neuronal diversity into artificial neural networks. Recently proposed quadratic neuron, which replaces the inner-product operation in conventional neurons with a quadratic one, have achieved great success in many essential tasks. Despite the promising results of quadratic neurons, there is still an unresolved issue: \textit{Is the superior performance of quadratic networks simply due to the increased parameters or due to the intrinsic expressive capability?} Without clarifying this issue, the performance of quadratic networks is always suspicious. Additionally, resolving this issue is reduced to finding killer applications of quadratic networks. In this paper, with theoretical and empirical studies, we show that quadratic networks enjoy parametric efficiency, thereby confirming that the superior performance of quadratic networks is due to the intrinsic expressive capability. This intrinsic expressive ability comes from that quadratic neurons can easily represent nonlinear interaction, while it is hard for conventional neurons. Theoretically, we derive the approximation efficiency of the quadratic network over conventional ones in terms of real space and manifolds. Moreover, from the perspective of the Barron space, we demonstrate that there exists a functional space whose functions can be approximated by quadratic networks in a dimension-free error, but the approximation error of conventional networks is dependent on dimensions. Empirically, experimental results on synthetic data, classic benchmarks, and real-world applications show that quadratic models broadly enjoy parametric efficiency, and the gain of efficiency depends on the task.