ReLU Network Approximation in Terms of Intrinsic Parameters
Paper and Code
Nov 15, 2021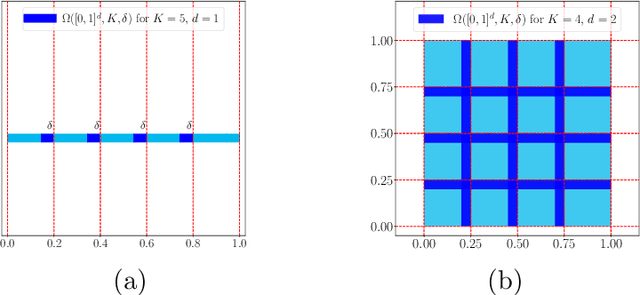
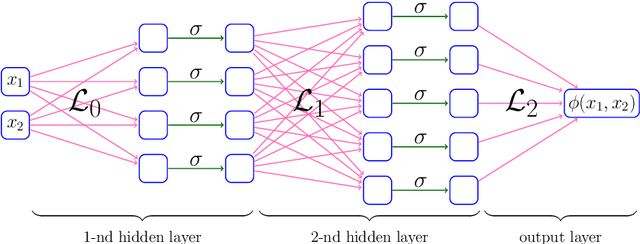
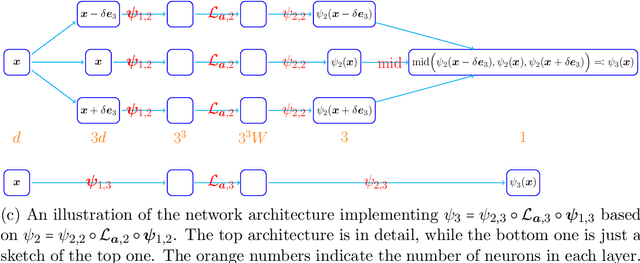
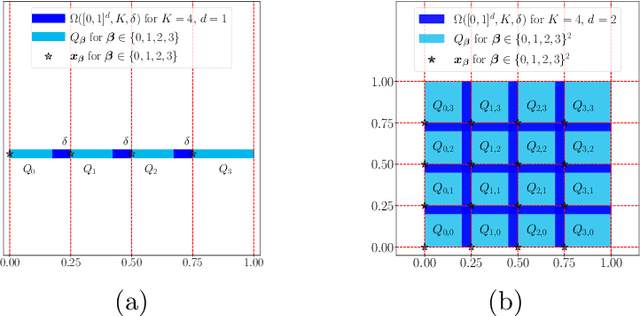
This paper studies the approximation error of ReLU networks in terms of the number of intrinsic parameters (i.e., those depending on the target function $f$). First, we prove by construction that, for any Lipschitz continuous function $f$ on $[0,1]^d$ with a Lipschitz constant $\lambda>0$, a ReLU network with $n+2$ intrinsic parameters can approximate $f$ with an exponentially small error $5\lambda \sqrt{d}\,2^{-n}$ measured in the $L^p$-norm for $p\in [1,\infty)$. More generally for an arbitrary continuous function $f$ on $[0,1]^d$ with a modulus of continuity $\omega_f(\cdot)$, the approximation error is $\omega_f(\sqrt{d}\, 2^{-n})+2^{-n+2}\omega_f(\sqrt{d})$. Next, we extend these two results from the $L^p$-norm to the $L^\infty$-norm at a price of $3^d n+2$ intrinsic parameters. Finally, by using a high-precision binary representation and the bit extraction technique via a fixed ReLU network independent of the target function, we design, theoretically, a ReLU network with only three intrinsic parameters to approximate H\"older continuous functions with an arbitrarily small error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge