Interpolation, Approximation and Controllability of Deep Neural Networks

We investigate the expressive power of deep residual neural networks idealized as continuous dynamical systems through control theory. Specifically, we consider two properties that arise from supervised learning, namely universal interpolation - the ability to match arbitrary input and target training samples - and the closely related notion of universal approximation - the ability to approximate input-target functional relationships via flow maps. Under the assumption of affine invariance of the control family, we give a characterisation of universal interpolation, showing that it holds for essentially any architecture with non-linearity. Furthermore, we elucidate the relationship between universal interpolation and universal approximation in the context of general control systems, showing that the two properties cannot be deduced from each other. At the same time, we identify conditions on the control family and the target function that ensures the equivalence of the two notions.

On the Universal Approximation Property of Deep Fully Convolutional Neural Networks

We study the approximation of shift-invariant or equivariant functions by deep fully convolutional networks from the dynamical systems perspective. We prove that deep residual fully convolutional networks and their continuous-layer counterpart can achieve universal approximation of these symmetric functions at constant channel width. Moreover, we show that the same can be achieved by non-residual variants with at least 2 channels in each layer and convolutional kernel size of at least 2. In addition, we show that these requirements are necessary, in the sense that networks with fewer channels or smaller kernels fail to be universal approximators.

Deep Neural Network Approximation of Invariant Functions through Dynamical Systems

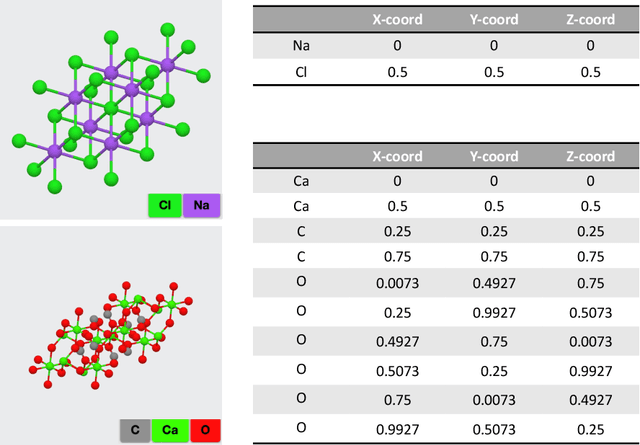
We study the approximation of functions which are invariant with respect to certain permutations of the input indices using flow maps of dynamical systems. Such invariant functions includes the much studied translation-invariant ones involving image tasks, but also encompasses many permutation-invariant functions that finds emerging applications in science and engineering. We prove sufficient conditions for universal approximation of these functions by a controlled equivariant dynamical system, which can be viewed as a general abstraction of deep residual networks with symmetry constraints. These results not only imply the universal approximation for a variety of commonly employed neural network architectures for symmetric function approximation, but also guide the design of architectures with approximation guarantees for applications involving new symmetry requirements.

Neural Network Architecture Beyond Width and Depth

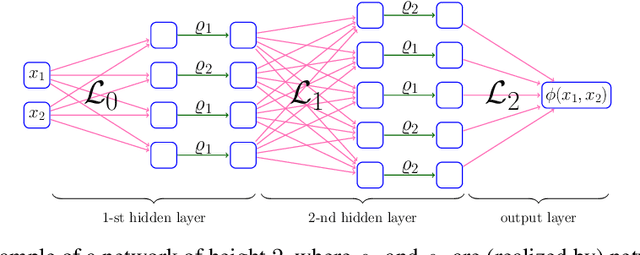
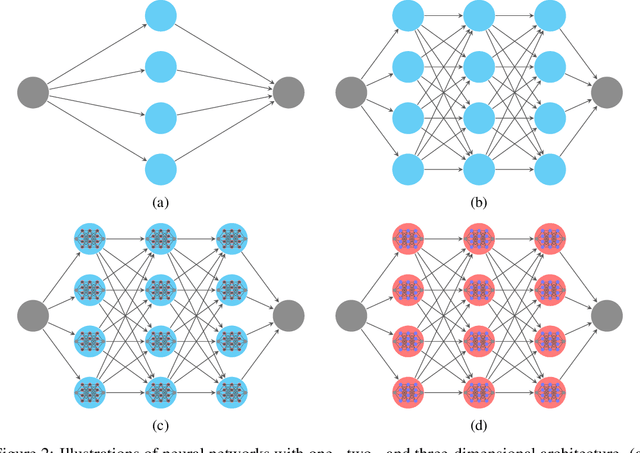
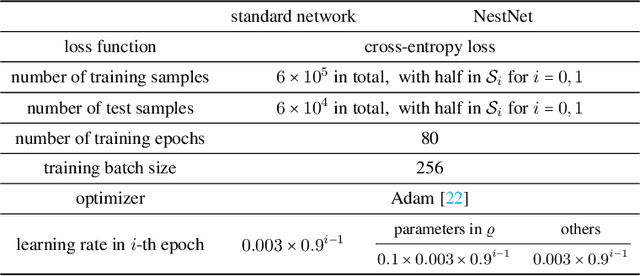
This paper proposes a new neural network architecture by introducing an additional dimension called height beyond width and depth. Neural network architectures with height, width, and depth as hyperparameters are called three-dimensional architectures. It is shown that neural networks with three-dimensional architectures are significantly more expressive than the ones with two-dimensional architectures (those with only width and depth as hyperparameters), e.g., standard fully connected networks. The new network architecture is constructed recursively via a nested structure, and hence we call a network with the new architecture nested network (NestNet). A NestNet of height $s$ is built with each hidden neuron activated by a NestNet of height $\le s-1$. When $s=1$, a NestNet degenerates to a standard network with a two-dimensional architecture. It is proved by construction that height-$s$ ReLU NestNets with $\mathcal{O}(n)$ parameters can approximate Lipschitz continuous functions on $[0,1]^d$ with an error $\mathcal{O}(n^{-(s+1)/d})$, while the optimal approximation error of standard ReLU networks with $\mathcal{O}(n)$ parameters is $\mathcal{O}(n^{-2/d})$. Furthermore, such a result is extended to generic continuous functions on $[0,1]^d$ with the approximation error characterized by the modulus of continuity. Finally, a numerical example is provided to explore the advantages of the super approximation power of ReLU NestNets.

IAE-Net: Integral Autoencoders for Discretization-Invariant Learning

Discretization invariant learning aims at learning in the infinite-dimensional function spaces with the capacity to process heterogeneous discrete representations of functions as inputs and/or outputs of a learning model. This paper proposes a novel deep learning framework based on integral autoencoders (IAE-Net) for discretization invariant learning. The basic building block of IAE-Net consists of an encoder and a decoder as integral transforms with data-driven kernels, and a fully connected neural network between the encoder and decoder. This basic building block is applied in parallel in a wide multi-channel structure, which are repeatedly composed to form a deep and densely connected neural network with skip connections as IAE-Net. IAE-Net is trained with randomized data augmentation that generates training data with heterogeneous structures to facilitate the performance of discretization invariant learning. The proposed IAE-Net is tested with various applications in predictive data science, solving forward and inverse problems in scientific computing, and signal/image processing. Compared with alternatives in the literature, IAE-Net achieves state-of-the-art performance in existing applications and creates a wide range of new applications.

ReLU Network Approximation in Terms of Intrinsic Parameters

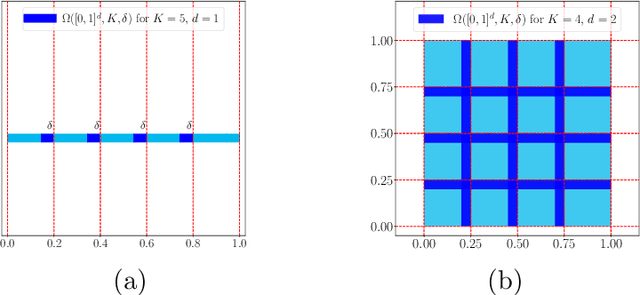
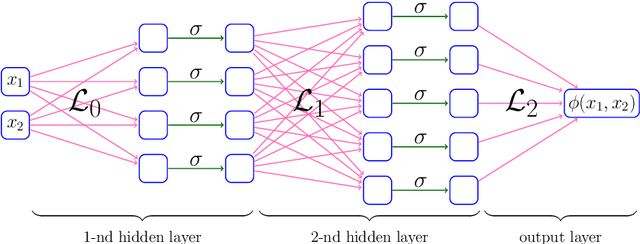
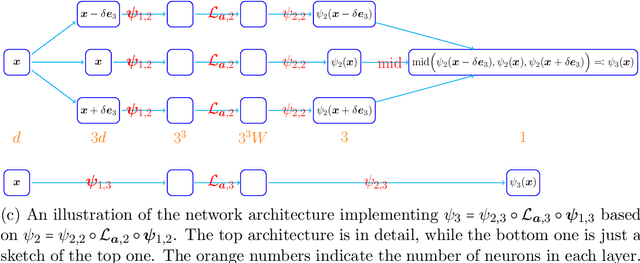
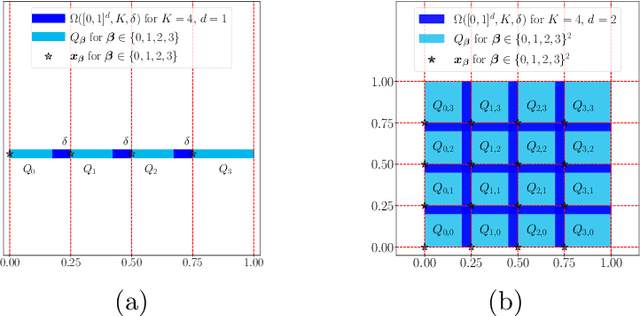
This paper studies the approximation error of ReLU networks in terms of the number of intrinsic parameters (i.e., those depending on the target function $f$). First, we prove by construction that, for any Lipschitz continuous function $f$ on $[0,1]^d$ with a Lipschitz constant $\lambda>0$, a ReLU network with $n+2$ intrinsic parameters can approximate $f$ with an exponentially small error $5\lambda \sqrt{d}\,2^{-n}$ measured in the $L^p$-norm for $p\in [1,\infty)$. More generally for an arbitrary continuous function $f$ on $[0,1]^d$ with a modulus of continuity $\omega_f(\cdot)$, the approximation error is $\omega_f(\sqrt{d}\, 2^{-n})+2^{-n+2}\omega_f(\sqrt{d})$. Next, we extend these two results from the $L^p$-norm to the $L^\infty$-norm at a price of $3^d n+2$ intrinsic parameters. Finally, by using a high-precision binary representation and the bit extraction technique via a fixed ReLU network independent of the target function, we design, theoretically, a ReLU network with only three intrinsic parameters to approximate H\"older continuous functions with an arbitrarily small error.

Deep Network Approximation: Achieving Arbitrary Accuracy with Fixed Number of Neurons

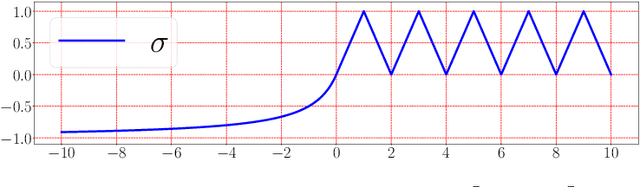
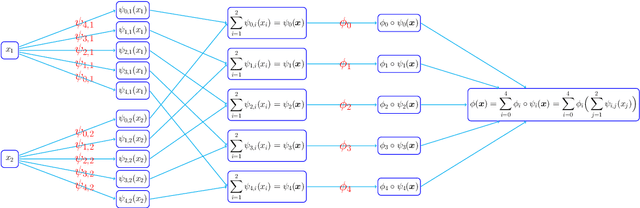
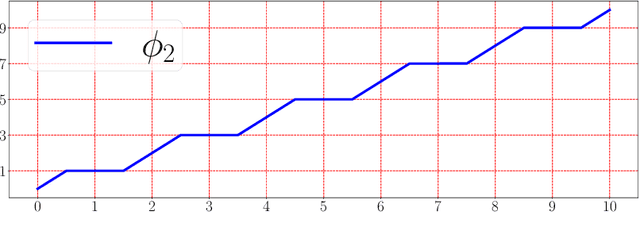
This paper develops simple feed-forward neural networks that achieve the universal approximation property for all continuous functions with a fixed finite number of neurons. These neural networks are simple because they are designed with a simple and computable continuous activation function $\sigma$ leveraging a triangular-wave function and a softsign function. We prove that $\sigma$-activated networks with width $36d(2d+1)$ and depth $11$ can approximate any continuous function on a $d$-dimensioanl hypercube within an arbitrarily small error. Hence, for supervised learning and its related regression problems, the hypothesis space generated by these networks with a size not smaller than $36d(2d+1)\times 11$ is dense in the space of continuous functions. Furthermore, classification functions arising from image and signal classification are in the hypothesis space generated by $\sigma$-activated networks with width $36d(2d+1)$ and depth $12$, when there exist pairwise disjoint closed bounded subsets of $\mathbb{R}^d$ such that the samples of the same class are located in the same subset.

Optimal Approximation Rate of ReLU Networks in terms of Width and Depth

This paper concentrates on the approximation power of deep feed-forward neural networks in terms of width and depth. It is proved by construction that ReLU networks with width $\mathcal{O}\big(\max\{d\lfloor N^{1/d}\rfloor,\, N+2\}\big)$ and depth $\mathcal{O}(L)$ can approximate a H\"older continuous function on $[0,1]^d$ with an approximation rate $\mathcal{O}\big(\lambda\sqrt{d} (N^2L^2\ln N)^{-\alpha/d}\big)$, where $\alpha\in (0,1]$ and $\lambda>0$ are H\"older order and constant, respectively. Such a rate is optimal up to a constant in terms of width and depth separately, while existing results are only nearly optimal without the logarithmic factor in the approximation rate. More generally, for an arbitrary continuous function $f$ on $[0,1]^d$, the approximation rate becomes $\mathcal{O}\big(\,\sqrt{d}\,\omega_f\big( (N^2L^2\ln N)^{-1/d}\big)\,\big)$, where $\omega_f(\cdot)$ is the modulus of continuity. We also extend our analysis to any continuous function $f$ on a bounded set. Particularly, if ReLU networks with depth $31$ and width $\mathcal{O}(N)$ are used to approximate one-dimensional Lipschitz continuous functions on $[0,1]$ with a Lipschitz constant $\lambda>0$, the approximation rate in terms of the total number of parameters, $W=\mathcal{O}(N^2)$, becomes $\mathcal{O}(\tfrac{\lambda}{W\ln W})$, which has not been discovered in the literature for fixed-depth ReLU networks.

Neural Network Approximation: Three Hidden Layers Are Enough

A three-hidden-layer neural network with super approximation power is introduced. This network is built with the Floor function ($\lfloor x\rfloor$), the exponential function ($2^x$), the step function ($\one_{x\geq 0}$), or their compositions as activation functions in each neuron and hence we call such networks as Floor-Exponential-Step (FLES) networks. For any width hyper-parameter $N\in\mathbb{N}^+$, it is shown that FLES networks with a width $\max\{d,\, N\}$ and three hidden layers can uniformly approximate a H{\"o}lder function $f$ on $[0,1]^d$ with an exponential approximation rate $3\lambda d^{\alpha/2}2^{-\alpha N}$, where $\alpha \in(0,1]$ and $\lambda$ are the H{\"o}lder order and constant, respectively. More generally for an arbitrary continuous function $f$ on $[0,1]^d$ with a modulus of continuity $\omega_f(\cdot)$, the constructive approximation rate is $\omega_f(\sqrt{d}\,2^{-N})+2\omega_f(\sqrt{d}){2^{-N}}$. As a consequence, this new {class of networks} overcomes the curse of dimensionality in approximation power when the variation of $\omega_f(r)$ as $r\rightarrow 0$ is moderate (e.g., $\omega_f(r){\lesssim} r^\alpha$ for H{\"o}lder continuous functions), since the major term to be concerned in our approximation rate is essentially $\sqrt{d}$ times a function of $N$ independent of $d$ within the modulus of continuity.

Deep Network Approximation with Discrepancy Being Reciprocal of Width to Power of Depth

A new network with super approximation power is introduced. This network is built with Floor ($\lfloor x\rfloor$) and ReLU ($\max\{0,x\}$) activation functions and hence we call such networks as Floor-ReLU networks. It is shown by construction that Floor-ReLU networks with width $\max\{d,\, 5N+13\}$ and depth $64dL+3$ can pointwise approximate a Lipschitz continuous function $f$ on $[0,1]^d$ with an exponential approximation rate $3\mu\sqrt{d}\,N^{-\sqrt{L}}$, where $\mu$ is the Lipschitz constant of $f$. More generally for an arbitrary continuous function $f$ on $[0,1]^d$ with a modulus of continuity $\omega_f(\cdot)$, the constructive approximation rate is $\omega_f(\sqrt{d}\,N^{-\sqrt{L}})+2\omega_f(\sqrt{d}){N^{-\sqrt{L}}}$. As a consequence, this new network overcomes the curse of dimensionality in approximation power since this approximation order is essentially $\sqrt{d}$ times a function of $N$ and $L$ independent of $d$.