Hamiltonian Monte Carlo Acceleration Using Surrogate Functions with Random Bases
Paper and Code
Apr 17, 2017
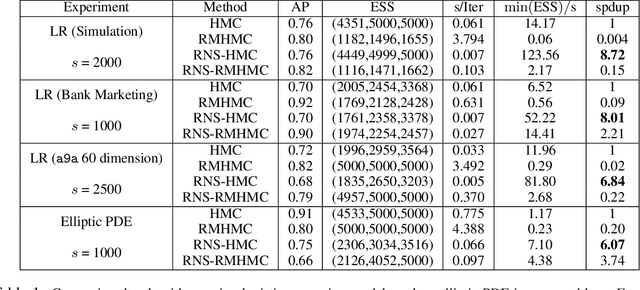
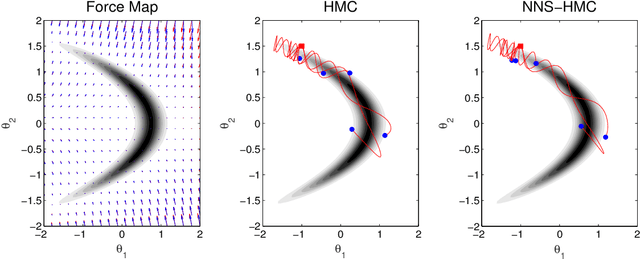

For big data analysis, high computational cost for Bayesian methods often limits their applications in practice. In recent years, there have been many attempts to improve computational efficiency of Bayesian inference. Here we propose an efficient and scalable computational technique for a state-of-the-art Markov Chain Monte Carlo (MCMC) methods, namely, Hamiltonian Monte Carlo (HMC). The key idea is to explore and exploit the structure and regularity in parameter space for the underlying probabilistic model to construct an effective approximation of its geometric properties. To this end, we build a surrogate function to approximate the target distribution using properly chosen random bases and an efficient optimization process. The resulting method provides a flexible, scalable, and efficient sampling algorithm, which converges to the correct target distribution. We show that by choosing the basis functions and optimization process differently, our method can be related to other approaches for the construction of surrogate functions such as generalized additive models or Gaussian process models. Experiments based on simulated and real data show that our approach leads to substantially more efficient sampling algorithms compared to existing state-of-the art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge