Hybrid Reinforcement Learning Framework for Mixed-Variable Problems

Optimization problems characterized by both discrete and continuous variables are common across various disciplines, presenting unique challenges due to their complex solution landscapes and the difficulty of navigating mixed-variable spaces effectively. To Address these challenges, we introduce a hybrid Reinforcement Learning (RL) framework that synergizes RL for discrete variable selection with Bayesian Optimization for continuous variable adjustment. This framework stands out by its strategic integration of RL and continuous optimization techniques, enabling it to dynamically adapt to the problem's mixed-variable nature. By employing RL for exploring discrete decision spaces and Bayesian Optimization to refine continuous parameters, our approach not only demonstrates flexibility but also enhances optimization performance. Our experiments on synthetic functions and real-world machine learning hyperparameter tuning tasks reveal that our method consistently outperforms traditional RL, random search, and standalone Bayesian optimization in terms of effectiveness and efficiency.

Path Planning in Unknown Environments Using Optimal Transport Theory

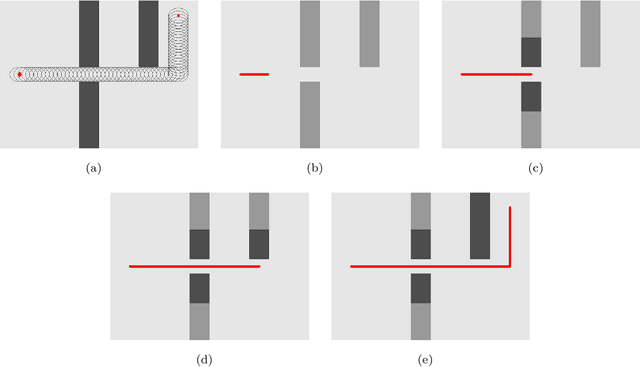
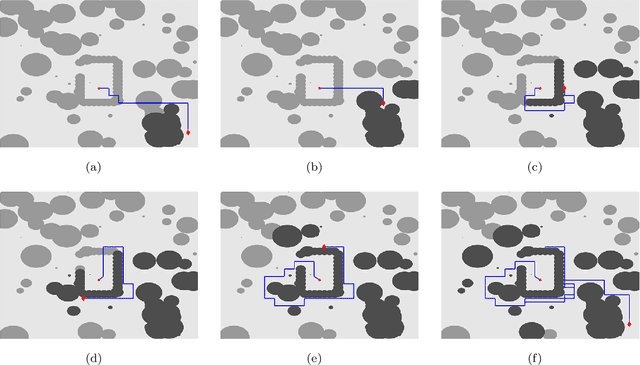
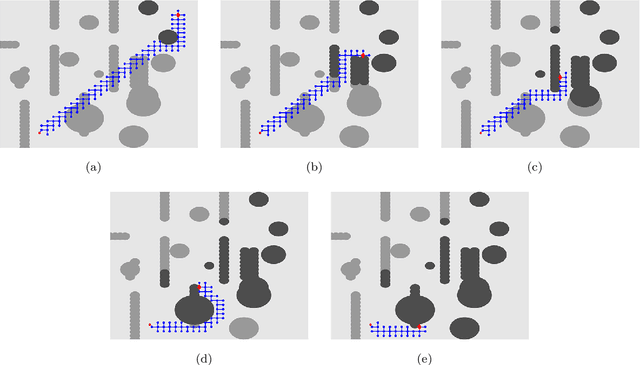
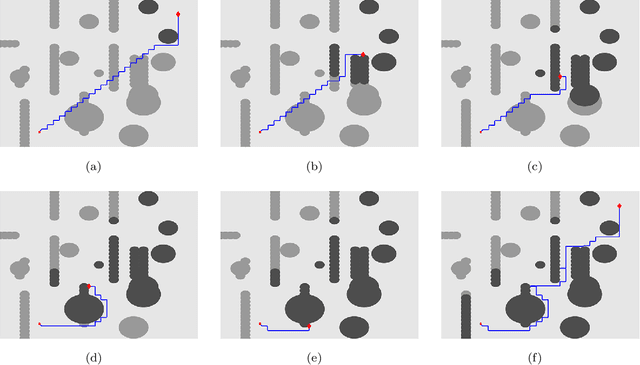
This paper introduces a graph-based, potential-guided method for path planning problems in unknown environments, where obstacles are unknown until the robots are in close proximity to the obstacle locations. Inspired by optimal transport theory, the proposed method generates a graph connecting the initial and target configurations, and then finds a path over the graph using the available environmental information. The graph and path are updated iteratively when newly encountered obstacle information becomes available. The resulting method is a deterministic procedure proven to be complete, i.e., it is guaranteed to find a feasible path, when one exists, in a finite number of iterations. The method is scalable to high-dimensional problems. In addition, our method does not search the entire domain for the path, instead, the algorithm only explores a sub-region that can be described by the evolution of the Fokker-Planck equation. We demonstrate the performance of our algorithm via several numerical examples with different environments and dimensions, including high-dimensional cases.

A cost-reducing partial labeling estimator in text classification problem

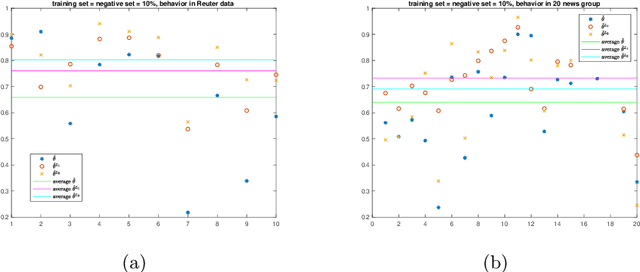
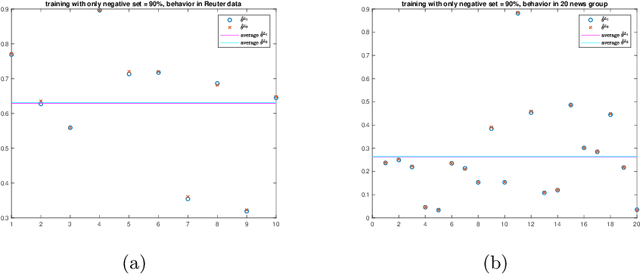
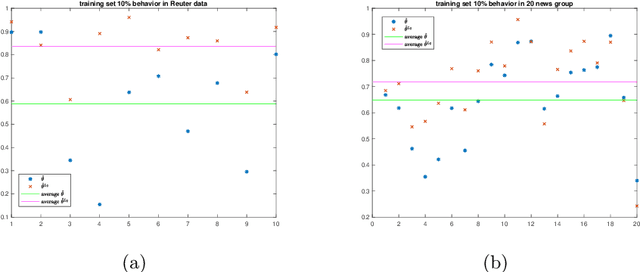
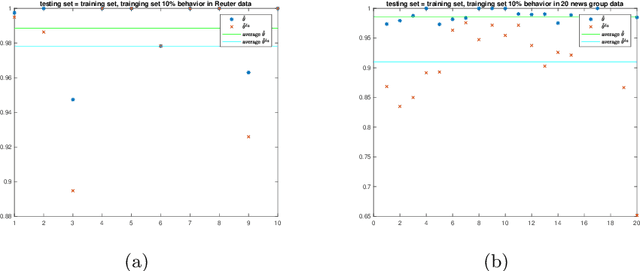
We propose a new approach to address the text classification problems when learning with partial labels is beneficial. Instead of offering each training sample a set of candidate labels, we assign negative-oriented labels to the ambiguous training examples if they are unlikely fall into certain classes. We construct our new maximum likelihood estimators with self-correction property, and prove that under some conditions, our estimators converge faster. Also we discuss the advantages of applying one of our estimator to a fully supervised learning problem. The proposed method has potential applicability in many areas, such as crowdsourcing, natural language processing and medical image analysis.

Centroid estimation based on symmetric KL divergence for Multinomial text classification problem

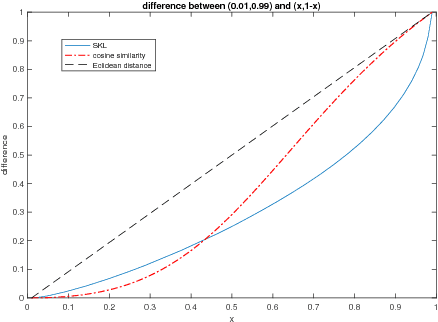
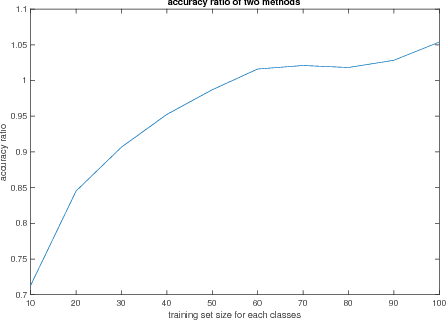
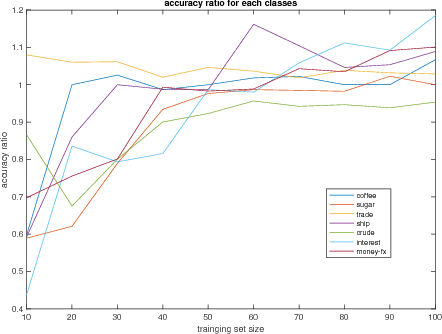
We define a new method to estimate centroid for text classification based on the symmetric KL-divergence between the distribution of words in training documents and their class centroids. Experiments on several standard data sets indicate that the new method achieves substantial improvements over the traditional classifiers.