Path Planning in Unknown Environments Using Optimal Transport Theory
Paper and Code
Sep 25, 2019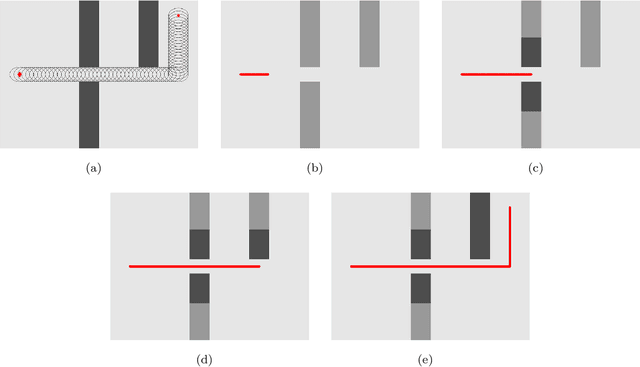
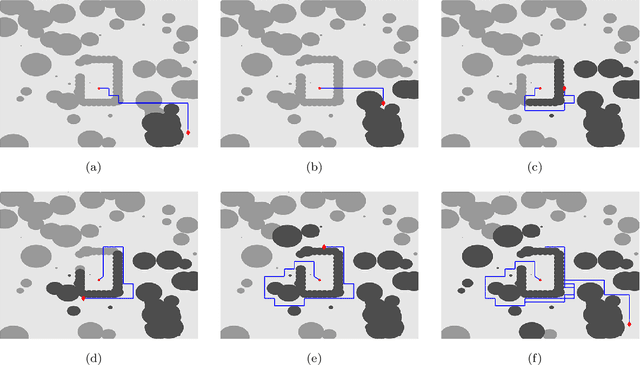
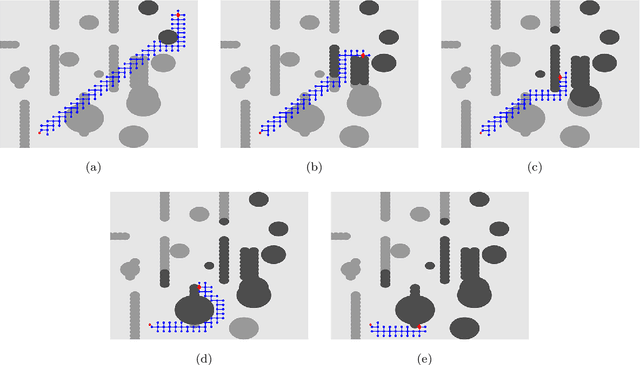
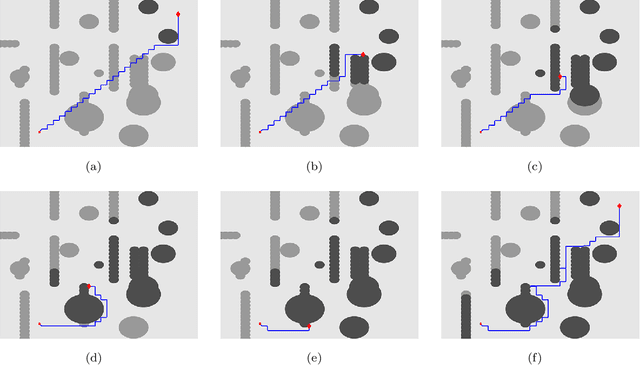
This paper introduces a graph-based, potential-guided method for path planning problems in unknown environments, where obstacles are unknown until the robots are in close proximity to the obstacle locations. Inspired by optimal transport theory, the proposed method generates a graph connecting the initial and target configurations, and then finds a path over the graph using the available environmental information. The graph and path are updated iteratively when newly encountered obstacle information becomes available. The resulting method is a deterministic procedure proven to be complete, i.e., it is guaranteed to find a feasible path, when one exists, in a finite number of iterations. The method is scalable to high-dimensional problems. In addition, our method does not search the entire domain for the path, instead, the algorithm only explores a sub-region that can be described by the evolution of the Fokker-Planck equation. We demonstrate the performance of our algorithm via several numerical examples with different environments and dimensions, including high-dimensional cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge