Improving Sampling Accuracy of Stochastic Gradient MCMC Methods via Non-uniform Subsampling of Gradients

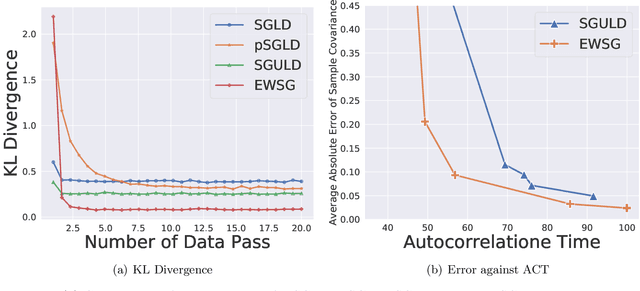
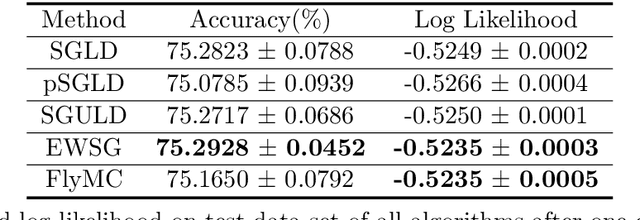
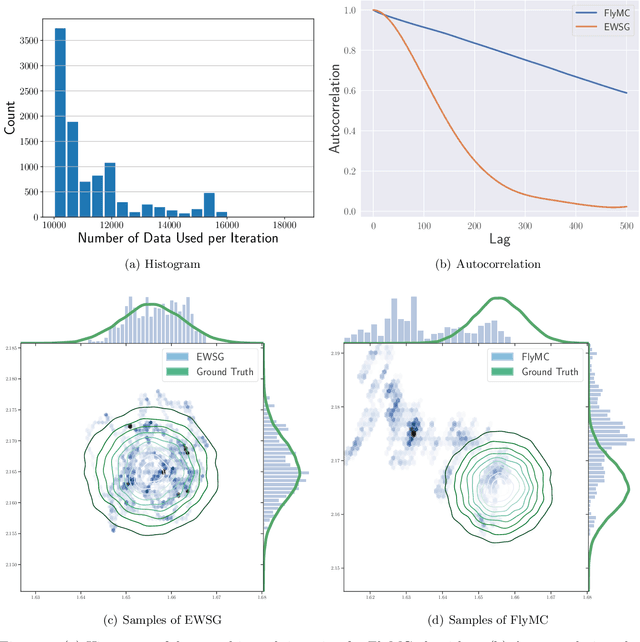
Common Stochastic Gradient MCMC methods approximate gradients by stochastic ones via uniformly subsampled data points. We propose that a non-uniform subsampling can reduce the variance introduced by the stochastic approximation, hence making the sampling of a target distribution more accurate. An exponentially weighted stochastic gradient approach (EWSG) is developed for this objective by matching the transition kernels of SG-MCMC methods respectively based on stochastic and batch gradients. A demonstration of EWSG combined with second-order Langevin equation for sampling purposes is provided. In our method, non-uniform subsampling is done efficiently via a Metropolis-Hasting chain on the data index, which is coupled to the sampling algorithm. The fact that our method has reduced local variance with high probability is theoretically analyzed. A non-asymptotic global error analysis is also presented. Numerical experiments based on both synthetic and real world data sets are also provided to demonstrate the efficacy of the proposed approaches. While statistical accuracy has improved, the speed of convergence was empirically observed to be at least comparable to the uniform version.