Hau-tieng Wu
Enhancing Missing Data Imputation of Non-stationary Signals with Harmonic Decomposition
Sep 08, 2023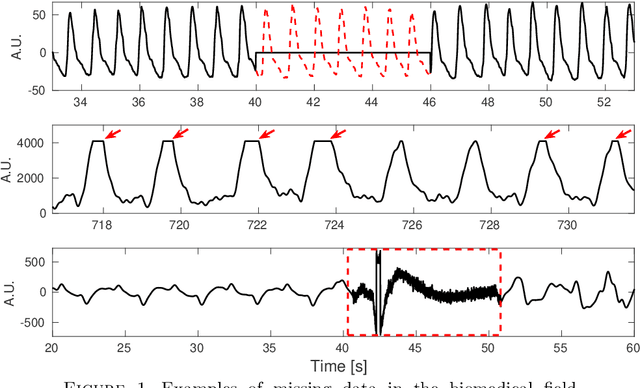
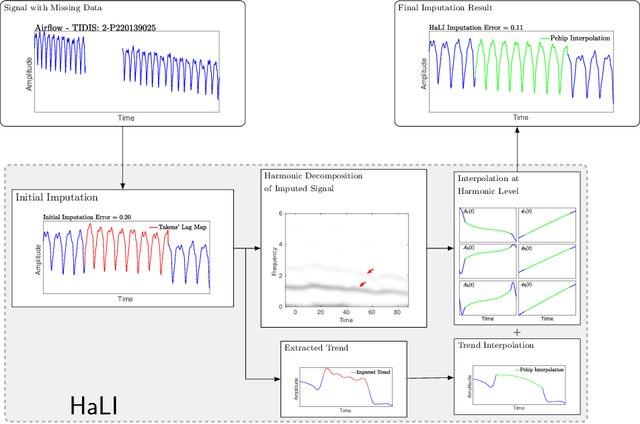
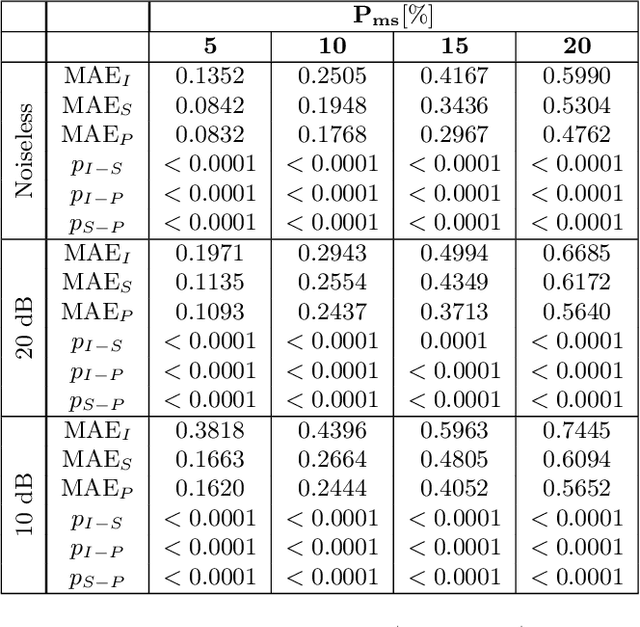
Abstract:Dealing with time series with missing values, including those afflicted by low quality or over-saturation, presents a significant signal processing challenge. The task of recovering these missing values, known as imputation, has led to the development of several algorithms. However, we have observed that the efficacy of these algorithms tends to diminish when the time series exhibit non-stationary oscillatory behavior. In this paper, we introduce a novel algorithm, coined Harmonic Level Interpolation (HaLI), which enhances the performance of existing imputation algorithms for oscillatory time series. After running any chosen imputation algorithm, HaLI leverages the harmonic decomposition based on the adaptive nonharmonic model of the initial imputation to improve the imputation accuracy for oscillatory time series. Experimental assessments conducted on synthetic and real signals consistently highlight that HaLI enhances the performance of existing imputation algorithms. The algorithm is made publicly available as a readily employable Matlab code for other researchers to use.
Sleep-wake classification via quantifying heart rate variability by convolutional neural network
Aug 01, 2018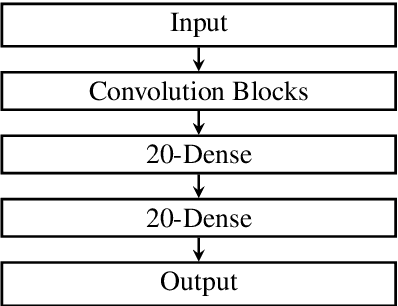

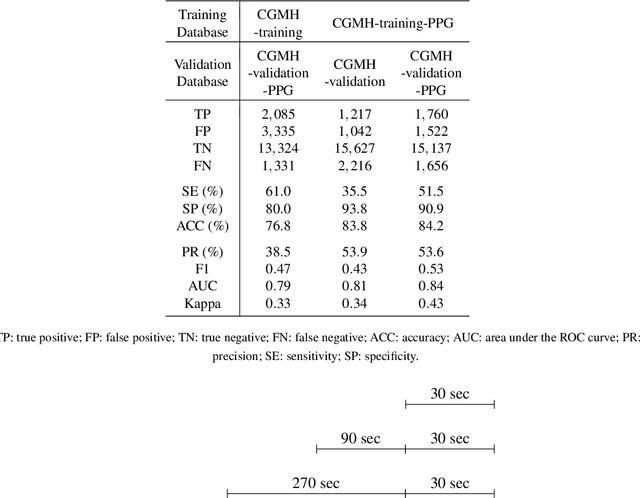
Abstract:Fluctuations in heart rate are intimately tied to changes in the physiological state of the organism. We examine and exploit this relationship by classifying a human subject's wake/sleep status using his instantaneous heart rate (IHR) series. We use a convolutional neural network (CNN) to build features from the IHR series extracted from a whole-night electrocardiogram (ECG) and predict every 30 seconds whether the subject is awake or asleep. Our training database consists of 56 normal subjects, and we consider three different databases for validation; one is private, and two are public with different races and apnea severities. On our private database of 27 subjects, our accuracy, sensitivity, specificity, and AUC values for predicting the wake stage are 83.1%, 52.4%, 89.4%, and 0.83, respectively. Validation performance is similar on our two public databases. When we use the photoplethysmography instead of the ECG to obtain the IHR series, the performance is also comparable. A robustness check is carried out to confirm the obtained performance statistics. This result advocates for an effective and scalable method for recognizing changes in physiological state using non-invasive heart rate monitoring. The CNN model adaptively quantifies IHR fluctuation as well as its location in time and is suitable for differentiating between the wake and sleep stages.
A Novel Blaschke Unwinding Adaptive Fourier Decomposition based Signal Compression Algorithm with Application on ECG Signals
Mar 17, 2018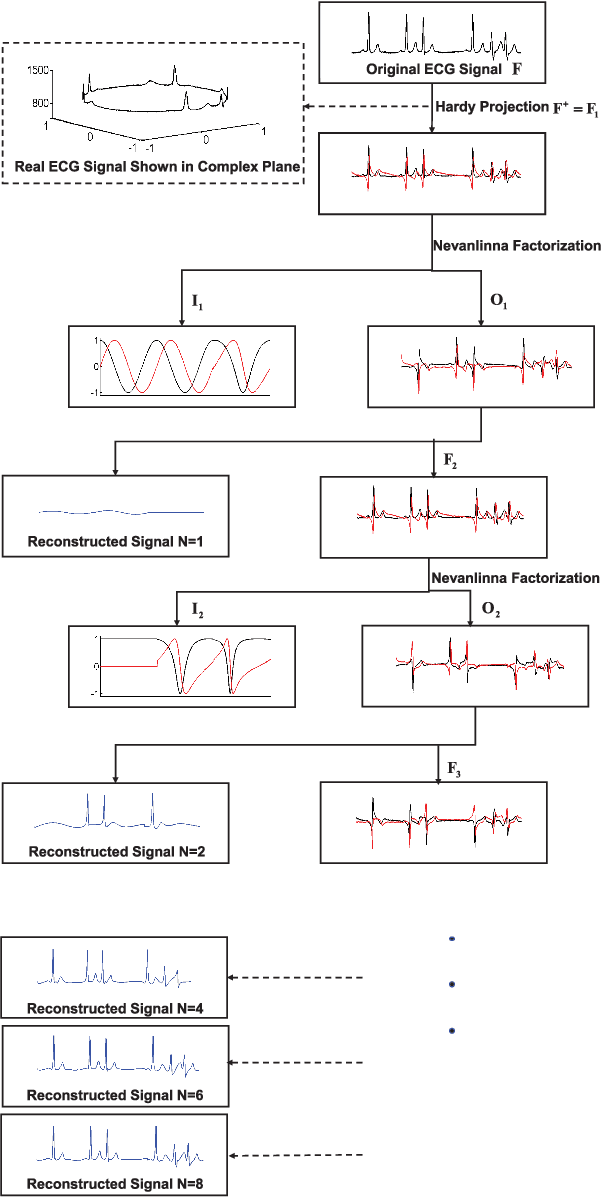
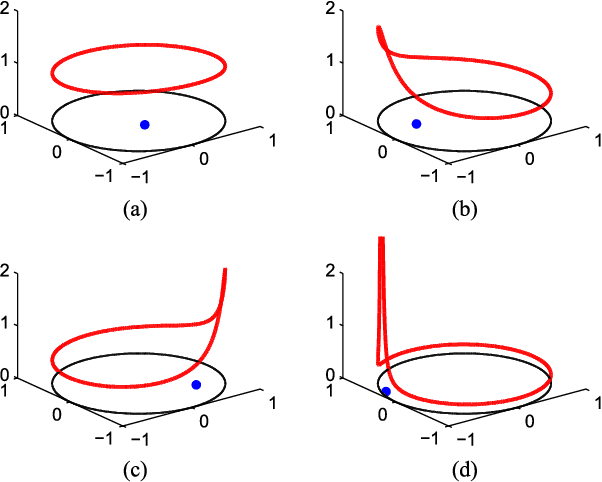
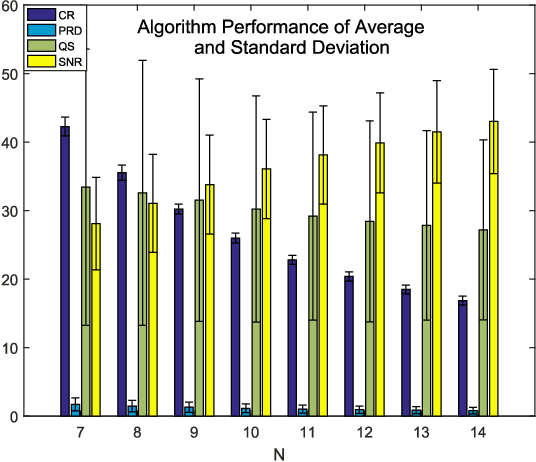
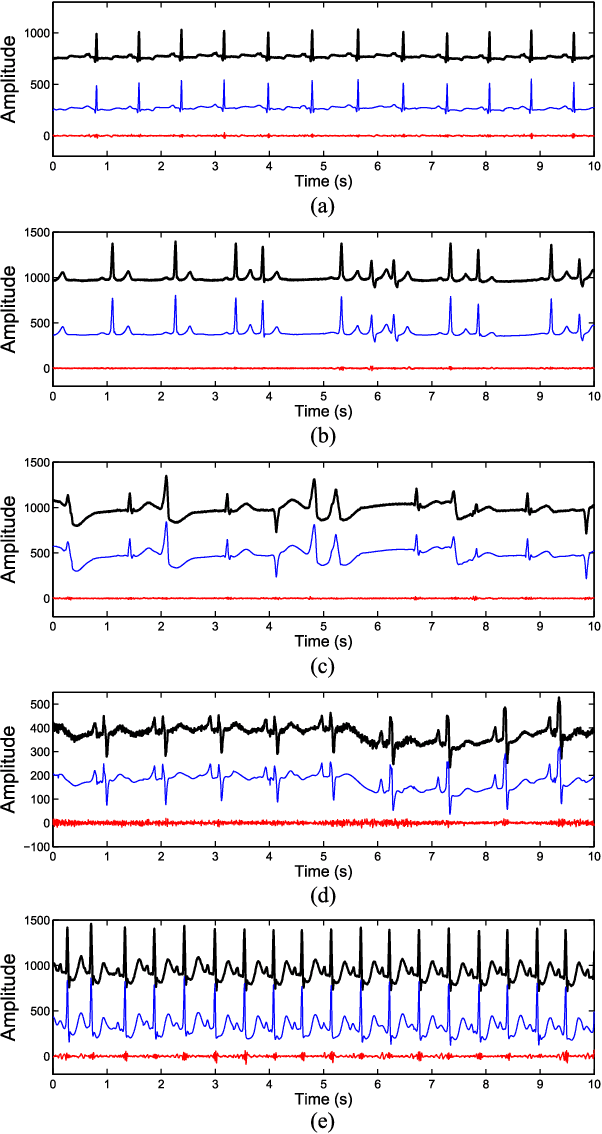
Abstract:This paper presents a novel signal compression algorithm based on the Blaschke unwinding adaptive Fourier decomposition (AFD). The Blaschke unwinding AFD is a newly developed signal decomposition theory. It utilizes the Nevanlinna factorization and the maximal selection principle in each decomposition step, and achieves a faster convergence rate with higher fidelity. The proposed compression algorithm is applied to the electrocardiogram signal. To assess the performance of the proposed compression algorithm, in addition to the generic assessment criteria, we consider the less discussed criteria related to the clinical needs -- for the heart rate variability analysis purpose, how accurate the R peak information is preserved is evaluated. The experiments are conducted on the MIT-BIH arrhythmia benchmark database. The results show that the proposed algorithm performs better than other state-of-the-art approaches. Meanwhile, it also well preserves the R peak information.
Embedding Riemannian Manifolds by the Heat Kernel of the Connection Laplacian
Sep 13, 2017Abstract:Given a class of closed Riemannian manifolds with prescribed geometric conditions, we introduce an embedding of the manifolds into $\ell^2$ based on the heat kernel of the Connection Laplacian associated with the Levi-Civita connection on the tangent bundle. As a result, we can construct a distance in this class which leads to a pre-compactness theorem on the class under consideration.
Latent common manifold learning with alternating diffusion: analysis and applications
Aug 03, 2017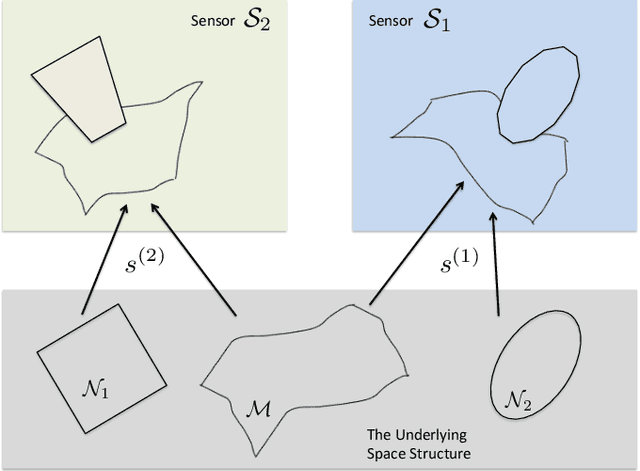

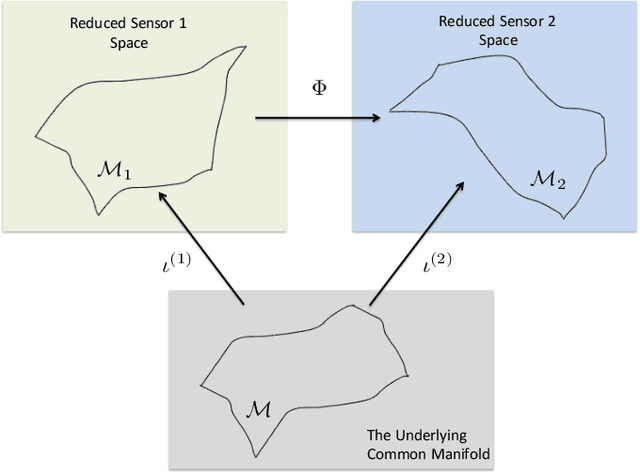
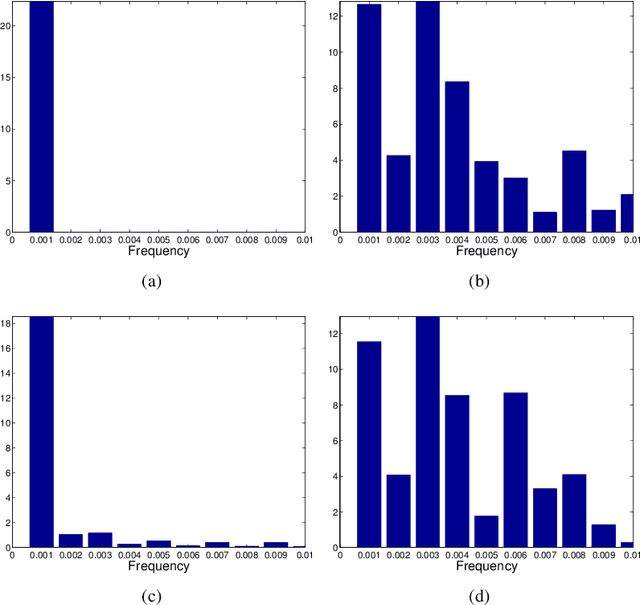
Abstract:The analysis of data sets arising from multiple sensors has drawn significant research attention over the years. Traditional methods, including kernel-based methods, are typically incapable of capturing nonlinear geometric structures. We introduce a latent common manifold model underlying multiple sensor observations for the purpose of multimodal data fusion. A method based on alternating diffusion is presented and analyzed; we provide theoretical analysis of the method under the latent common manifold model. To exemplify the power of the proposed framework, experimental results in several applications are reported.
Efficient fetal-maternal ECG signal separation from two channel maternal abdominal ECG via diffusion-based channel selection
Feb 07, 2017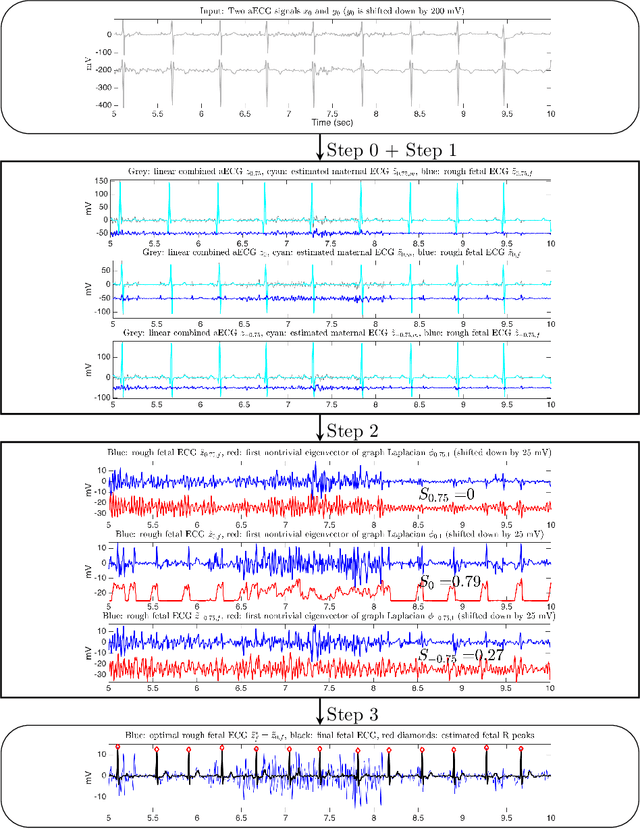
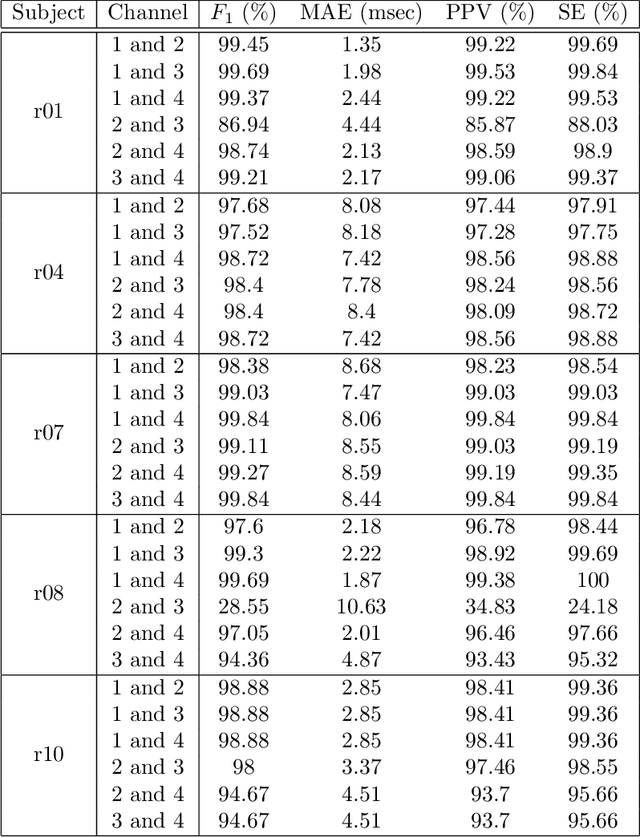
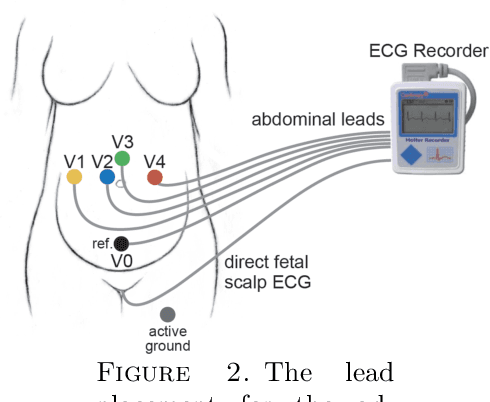
Abstract:There is a need for affordable, widely deployable maternal-fetal ECG monitors to improve maternal and fetal health during pregnancy and delivery. Based on the diffusion-based channel selection, here we present the mathematical formalism and clinical validation of an algorithm capable of accurate separation of maternal and fetal ECG from a two channel signal acquired over maternal abdomen.
Extract fetal ECG from single-lead abdominal ECG by de-shape short time Fourier transform and nonlocal median
Sep 09, 2016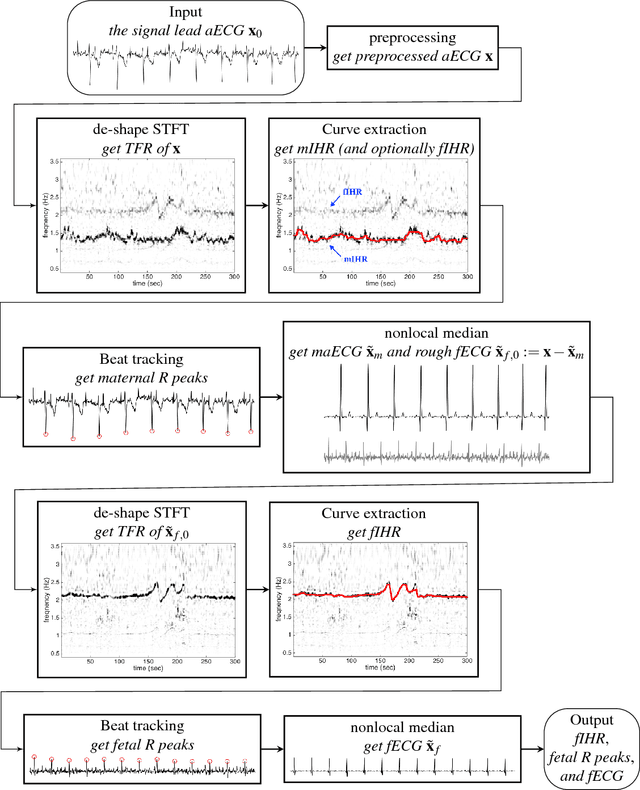
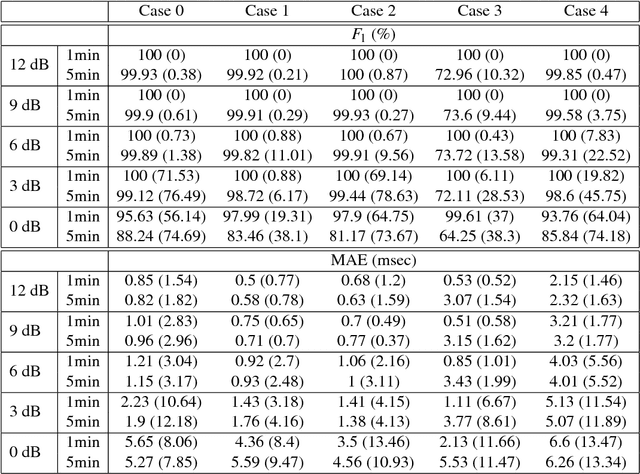
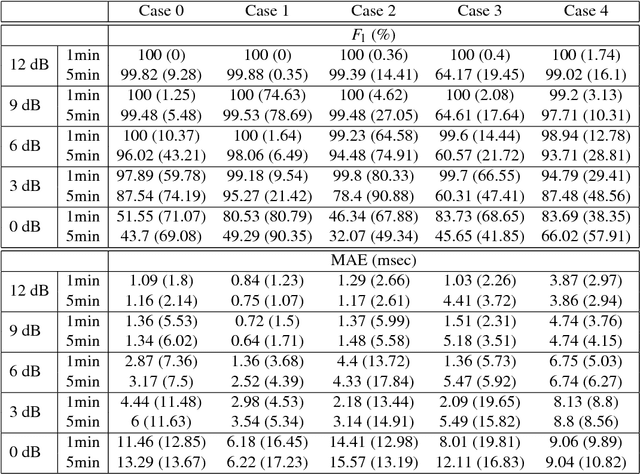

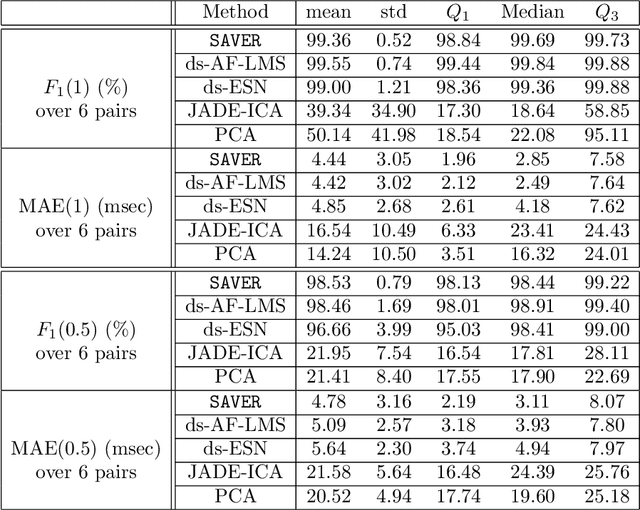
Abstract:The multiple fundamental frequency detection problem and the source separation problem from a single-channel signal containing multiple oscillatory components and a nonstationary noise are both challenging tasks. To extract the fetal electrocardiogram (ECG) from a single-lead maternal abdominal ECG, we face both challenges. In this paper, we propose a novel method to extract the fetal ECG signal from the single channel maternal abdominal ECG signal, without any additional measurement. The algorithm is composed of three main ingredients. First, the maternal and fetal heart rates are estimated by the de-shape short time Fourier transform, which is a recently proposed nonlinear time-frequency analysis technique; second, the beat tracking technique is applied to accurately obtain the maternal and fetal R peaks; third, the maternal and fetal ECG waveforms are established by the nonlocal median. The algorithm is evaluated on a simulated fetal ECG signal database ({\em fecgsyn} database), and tested on two real databases with the annotation provided by experts ({\em adfecgdb} database and {\em CinC2013} database). In general, the algorithm could be applied to solve other detection and source separation problems, and reconstruct the time-varying wave-shape function of each oscillatory component.
Spectral Convergence of the connection Laplacian from random samples
May 31, 2015Abstract:Spectral methods that are based on eigenvectors and eigenvalues of discrete graph Laplacians, such as Diffusion Maps and Laplacian Eigenmaps are often used for manifold learning and non-linear dimensionality reduction. It was previously shown by Belkin and Niyogi \cite{belkin_niyogi:2007} that the eigenvectors and eigenvalues of the graph Laplacian converge to the eigenfunctions and eigenvalues of the Laplace-Beltrami operator of the manifold in the limit of infinitely many data points sampled independently from the uniform distribution over the manifold. Recently, we introduced Vector Diffusion Maps and showed that the connection Laplacian of the tangent bundle of the manifold can be approximated from random samples. In this paper, we present a unified framework for approximating other connection Laplacians over the manifold by considering its principle bundle structure. We prove that the eigenvectors and eigenvalues of these Laplacians converge in the limit of infinitely many independent random samples. We generalize the spectral convergence results to the case where the data points are sampled from a non-uniform distribution, and for manifolds with and without boundary.
Graph connection Laplacian and random matrices with random blocks
Nov 16, 2014



Abstract:Graph connection Laplacian (GCL) is a modern data analysis technique that is starting to be applied for the analysis of high dimensional and massive datasets. Motivated by this technique, we study matrices that are akin to the ones appearing in the null case of GCL, i.e the case where there is no structure in the dataset under investigation. Developing this understanding is important in making sense of the output of the algorithms based on GCL. We hence develop a theory explaining the behavior of the spectral distribution of a large class of random matrices, in particular random matrices with random block entries of fixed size. Part of the theory covers the case where there is significant dependence between the blocks. Numerical work shows that the agreement between our theoretical predictions and numerical simulations is generally very good.
Connection graph Laplacian methods can be made robust to noise
May 23, 2014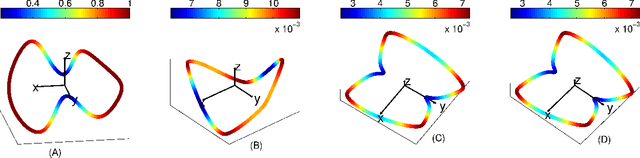
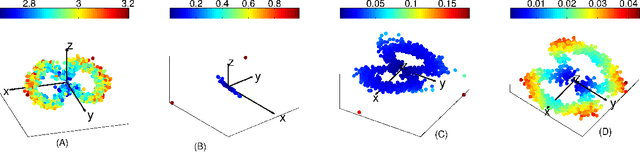


Abstract:Recently, several data analytic techniques based on connection graph laplacian (CGL) ideas have appeared in the literature. At this point, the properties of these methods are starting to be understood in the setting where the data is observed without noise. We study the impact of additive noise on these methods, and show that they are remarkably robust. As a by-product of our analysis, we propose modifications of the standard algorithms that increase their robustness to noise. We illustrate our results in numerical simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge