Latent common manifold learning with alternating diffusion: analysis and applications
Paper and Code
Aug 03, 2017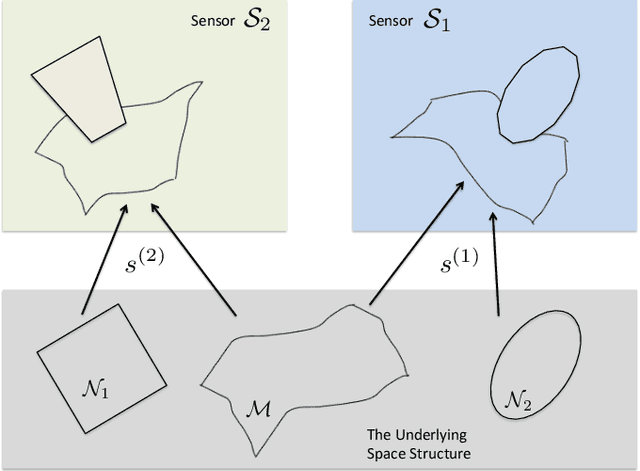

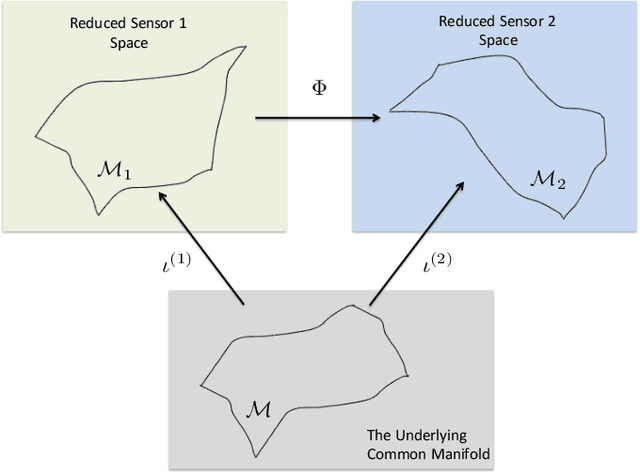
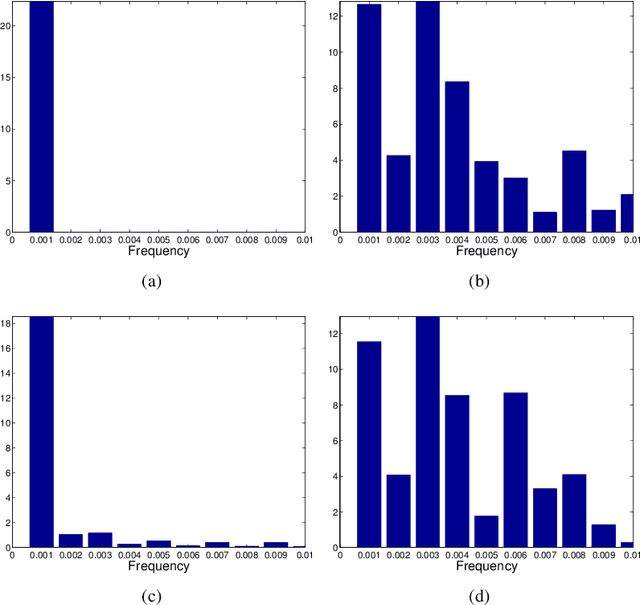
The analysis of data sets arising from multiple sensors has drawn significant research attention over the years. Traditional methods, including kernel-based methods, are typically incapable of capturing nonlinear geometric structures. We introduce a latent common manifold model underlying multiple sensor observations for the purpose of multimodal data fusion. A method based on alternating diffusion is presented and analyzed; we provide theoretical analysis of the method under the latent common manifold model. To exemplify the power of the proposed framework, experimental results in several applications are reported.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge