Wave-shape Function Model Order Estimation by Trigonometric Regression

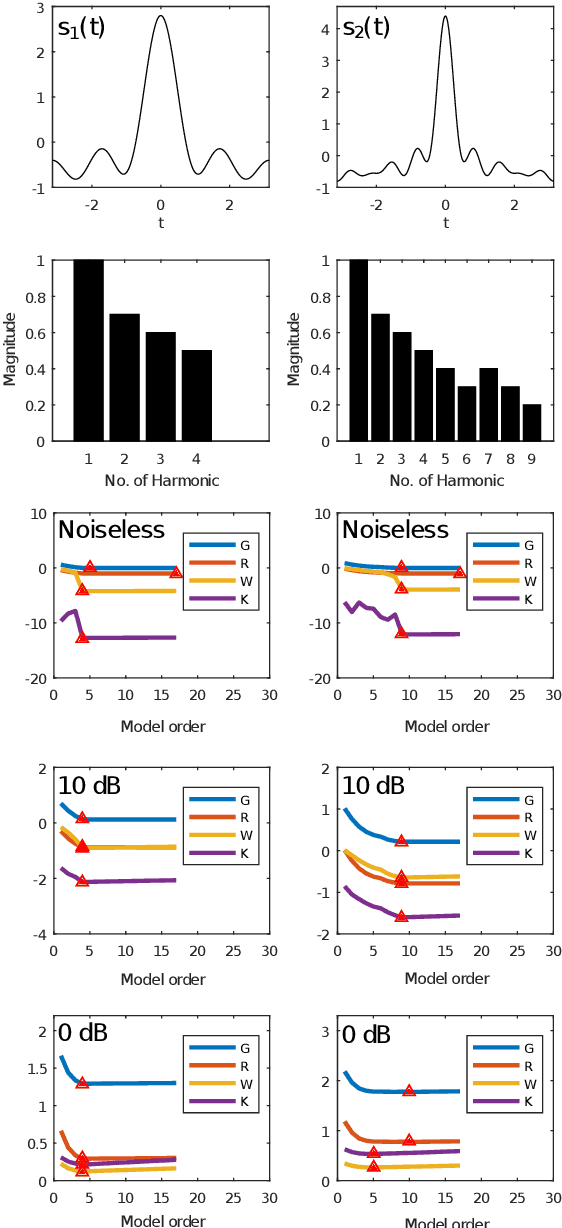
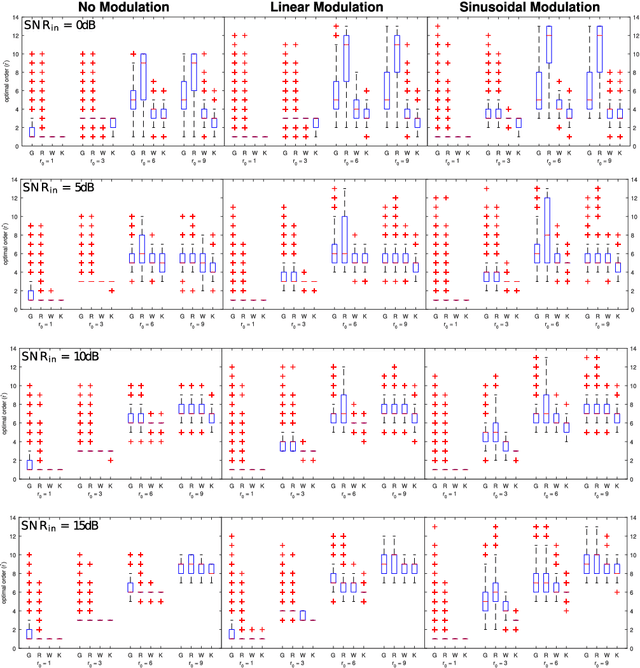
The adaptive non-harmonic (ANH) model is a powerful tool to compactly represent oscillating signals with time-varying amplitude and phase, and non-sinusoidal oscillating morphology. Given good estimators of instantaneous amplitude and phase we can construct an adaptive model, where the morphology of the oscillation is described by the wave-shape function (WSF), a 2{\pi}-periodic more general periodic function. In this paper, we address the problem of estimating the number of harmonic components of the WSF, a problem that remains underresearched, by adapting trigonometric regression model selection criteria into this context. We study the application of these criteria, originally developed in the context of stationary signals, to the case of signals with time-varying amplitudes and phases. We then incorporate the order estimation to the ANH model reconstruction procedure and analyze its performance for noisy AM-FM signals. Experimental results on synthethic signals indicate that these criteria enable the adaptive estimation of the waveform of non-stationary signals with non-sinusoidal oscillatory patterns, even in the presence of considerable amount of noise. We also apply our reconstruction procedure to the task of denoising simulated pulse wave signals and determine that the proposed technique performs competitively to other denoising schemes. We conclude this work by showing that our adaptive order estimation algorithm takes into account the interpatient waveform variability of the electrocardiogram (ECG) and respiratory signals by analyzing recordings from the Fantasia Database.

Fully Adaptive Time-Varying Wave-Shape Model: Applications in Biomedical Signal Processing

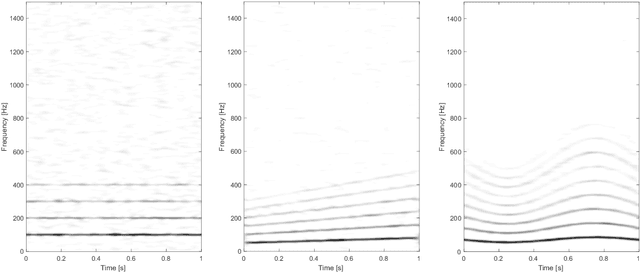
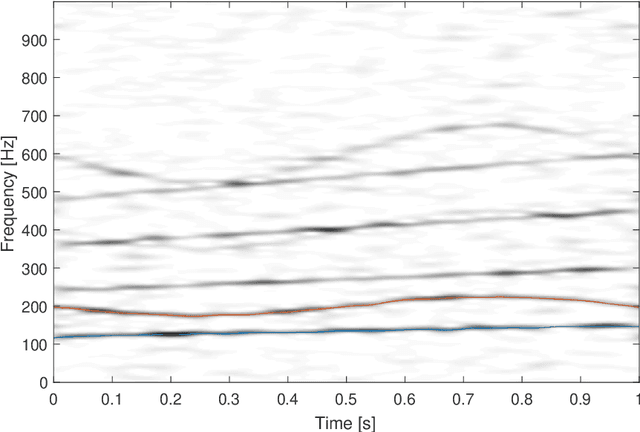
In this work, we propose a time-varying wave-shape extraction algorithm based on a modified version of the adaptive non-harmonic model for non-stationary signals. The model codifies the time-varying wave-shape information in the relative amplitude and phase of the harmonic components of the wave-shape. The algorithm was validated on both real and synthetic signals for the tasks of denoising, decomposition and adaptive segmentation. For the denoising task, both monocomponent and multicomponent synthetic signals were considered. In both cases, the proposed algorithm can accurately recover the time-varying wave-shape of non-stationary signals, even in the presence of high levels of noise, outperforming existing wave-shape estimation algorithms and denoising methods based on short-time Fourier transform thresholding. The denoising of an electroencephalograph signal was also performed, giving similar results. For decomposition, our proposal was able to recover the composing waveforms more accurately by considering the time variations from the harmonic amplitude functions when compared to existing methods. Finally, the algorithm was used for the adaptive segmentation of synthetic signals and an electrocardiograph of a patient undergoing ventricular fibrillation.

Enhancing Missing Data Imputation of Non-stationary Signals with Harmonic Decomposition

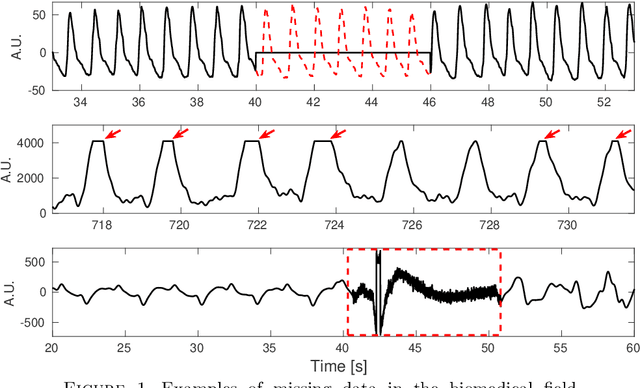
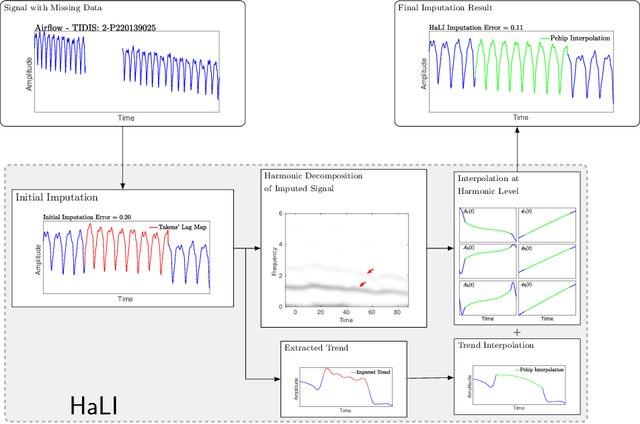
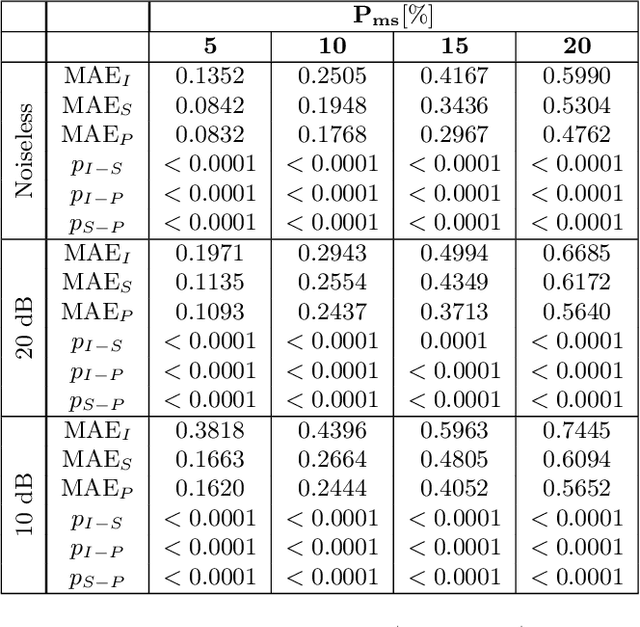
Dealing with time series with missing values, including those afflicted by low quality or over-saturation, presents a significant signal processing challenge. The task of recovering these missing values, known as imputation, has led to the development of several algorithms. However, we have observed that the efficacy of these algorithms tends to diminish when the time series exhibit non-stationary oscillatory behavior. In this paper, we introduce a novel algorithm, coined Harmonic Level Interpolation (HaLI), which enhances the performance of existing imputation algorithms for oscillatory time series. After running any chosen imputation algorithm, HaLI leverages the harmonic decomposition based on the adaptive nonharmonic model of the initial imputation to improve the imputation accuracy for oscillatory time series. Experimental assessments conducted on synthetic and real signals consistently highlight that HaLI enhances the performance of existing imputation algorithms. The algorithm is made publicly available as a readily employable Matlab code for other researchers to use.