Wave-shape Function Model Order Estimation by Trigonometric Regression

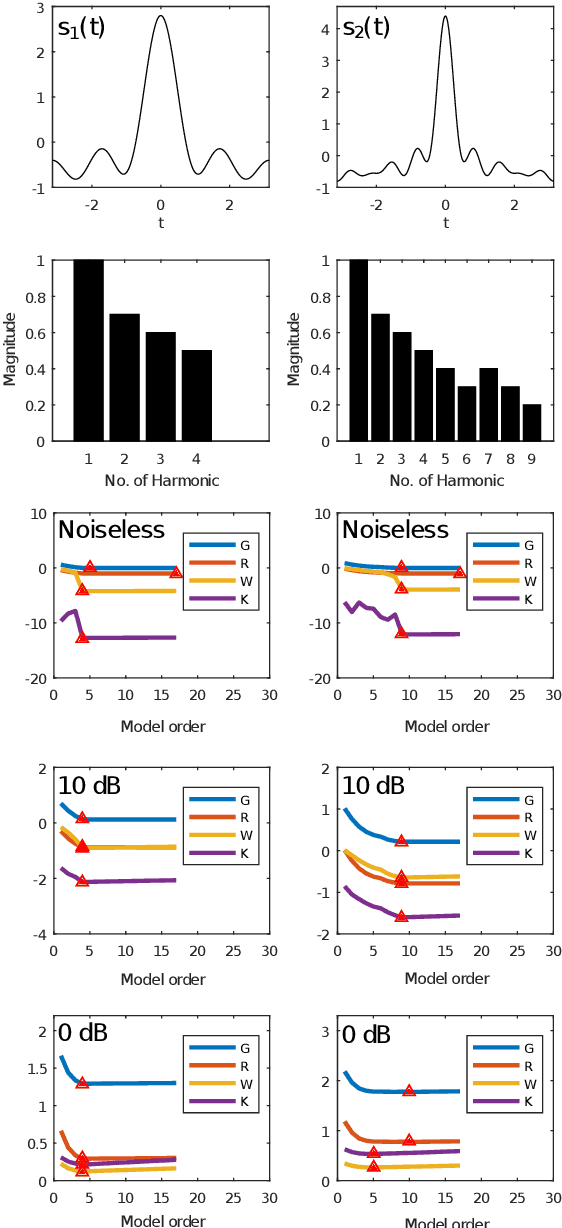
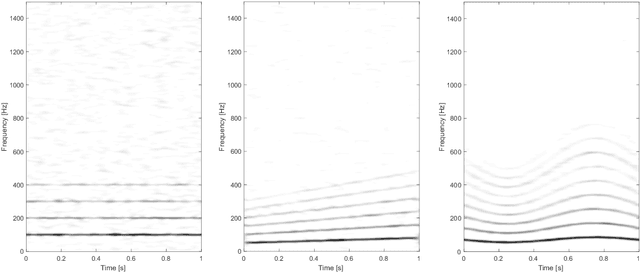
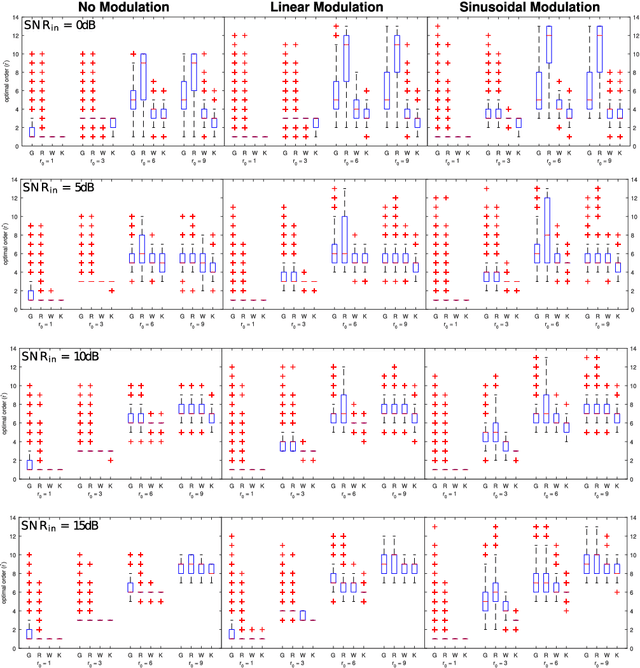
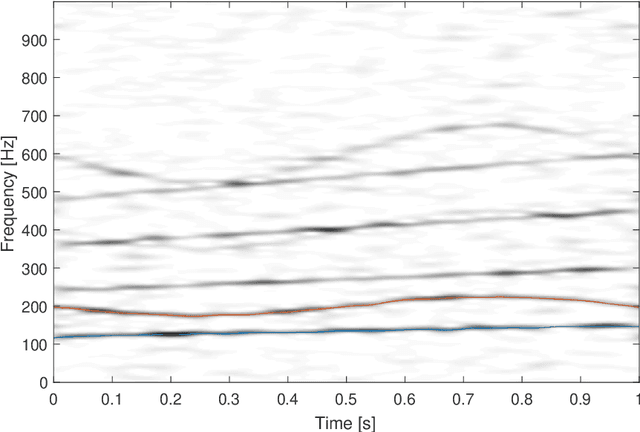
The adaptive non-harmonic (ANH) model is a powerful tool to compactly represent oscillating signals with time-varying amplitude and phase, and non-sinusoidal oscillating morphology. Given good estimators of instantaneous amplitude and phase we can construct an adaptive model, where the morphology of the oscillation is described by the wave-shape function (WSF), a 2{\pi}-periodic more general periodic function. In this paper, we address the problem of estimating the number of harmonic components of the WSF, a problem that remains underresearched, by adapting trigonometric regression model selection criteria into this context. We study the application of these criteria, originally developed in the context of stationary signals, to the case of signals with time-varying amplitudes and phases. We then incorporate the order estimation to the ANH model reconstruction procedure and analyze its performance for noisy AM-FM signals. Experimental results on synthethic signals indicate that these criteria enable the adaptive estimation of the waveform of non-stationary signals with non-sinusoidal oscillatory patterns, even in the presence of considerable amount of noise. We also apply our reconstruction procedure to the task of denoising simulated pulse wave signals and determine that the proposed technique performs competitively to other denoising schemes. We conclude this work by showing that our adaptive order estimation algorithm takes into account the interpatient waveform variability of the electrocardiogram (ECG) and respiratory signals by analyzing recordings from the Fantasia Database.