Adam symmetry theorem: characterization of the convergence of the stochastic Adam optimizer

Beside the standard stochastic gradient descent (SGD) method, the Adam optimizer due to Kingma & Ba (2014) is currently probably the best-known optimization method for the training of deep neural networks in artificial intelligence (AI) systems. Despite the popularity and the success of Adam it remains an \emph{open research problem} to provide a rigorous convergence analysis for Adam even for the class of strongly convex SOPs. In one of the main results of this work we establish convergence rates for Adam in terms of the number of gradient steps (convergence rate \nicefrac{1}{2} w.r.t. the size of the learning rate), the size of the mini-batches (convergence rate 1 w.r.t. the size of the mini-batches), and the size of the second moment parameter of Adam (convergence rate 1 w.r.t. the distance of the second moment parameter to 1) for the class of strongly convex SOPs. In a further main result of this work, which we refer to as \emph{Adam symmetry theorem}, we illustrate the optimality of the established convergence rates by proving for a special class of simple quadratic strongly convex SOPs that Adam converges as the number of gradient steps increases to infinity to the solution of the SOP (the unique minimizer of the strongly convex objective function) if and \emph{only} if the random variables in the SOP (the data in the SOP) are \emph{symmetrically distributed}. In particular, in the standard case where the random variables in the SOP are not symmetrically distributed we \emph{disprove} that Adam converges to the minimizer of the SOP as the number of Adam steps increases to infinity. We also complement the conclusions of our convergence analysis and the Adam symmetry theorem by several numerical simulations that indicate the sharpness of the established convergence rates and that illustrate the practical appearance of the phenomena revealed in the \emph{Adam symmetry theorem}.

An overview of diffusion models for generative artificial intelligence

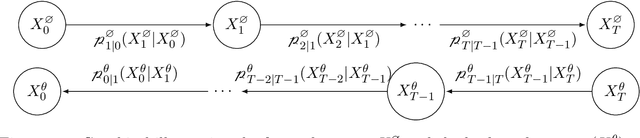
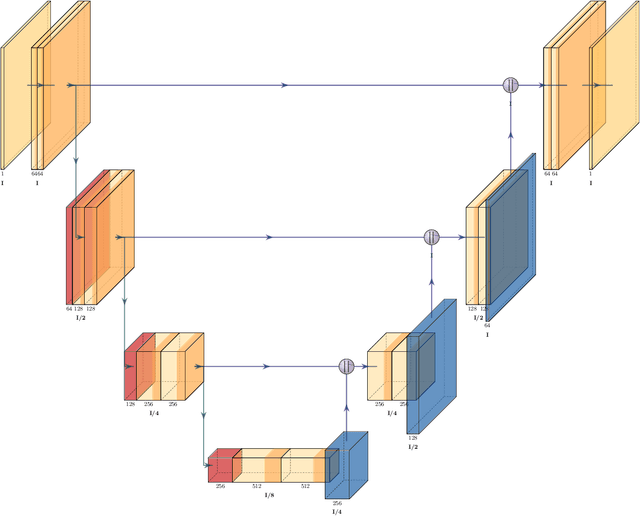
This article provides a mathematically rigorous introduction to denoising diffusion probabilistic models (DDPMs), sometimes also referred to as diffusion probabilistic models or diffusion models, for generative artificial intelligence. We provide a detailed basic mathematical framework for DDPMs and explain the main ideas behind training and generation procedures. In this overview article we also review selected extensions and improvements of the basic framework from the literature such as improved DDPMs, denoising diffusion implicit models, classifier-free diffusion guidance models, and latent diffusion models.

An Overview on Machine Learning Methods for Partial Differential Equations: from Physics Informed Neural Networks to Deep Operator Learning

The approximation of solutions of partial differential equations (PDEs) with numerical algorithms is a central topic in applied mathematics. For many decades, various types of methods for this purpose have been developed and extensively studied. One class of methods which has received a lot of attention in recent years are machine learning-based methods, which typically involve the training of artificial neural networks (ANNs) by means of stochastic gradient descent type optimization methods. While approximation methods for PDEs using ANNs have first been proposed in the 1990s they have only gained wide popularity in the last decade with the rise of deep learning. This article aims to provide an introduction to some of these methods and the mathematical theory on which they are based. We discuss methods such as physics-informed neural networks (PINNs) and deep BSDE methods and consider several operator learning approaches.

Mathematical Introduction to Deep Learning: Methods, Implementations, and Theory

This book aims to provide an introduction to the topic of deep learning algorithms. We review essential components of deep learning algorithms in full mathematical detail including different artificial neural network (ANN) architectures (such as fully-connected feedforward ANNs, convolutional ANNs, recurrent ANNs, residual ANNs, and ANNs with batch normalization) and different optimization algorithms (such as the basic stochastic gradient descent (SGD) method, accelerated methods, and adaptive methods). We also cover several theoretical aspects of deep learning algorithms such as approximation capacities of ANNs (including a calculus for ANNs), optimization theory (including Kurdyka-{\L}ojasiewicz inequalities), and generalization errors. In the last part of the book some deep learning approximation methods for PDEs are reviewed including physics-informed neural networks (PINNs) and deep Galerkin methods. We hope that this book will be useful for students and scientists who do not yet have any background in deep learning at all and would like to gain a solid foundation as well as for practitioners who would like to obtain a firmer mathematical understanding of the objects and methods considered in deep learning.

Algorithmically Designed Artificial Neural Networks (ADANNs): Higher order deep operator learning for parametric partial differential equations

In this article we propose a new deep learning approach to solve parametric partial differential equations (PDEs) approximately. In particular, we introduce a new strategy to design specific artificial neural network (ANN) architectures in conjunction with specific ANN initialization schemes which are tailor-made for the particular scientific computing approximation problem under consideration. In the proposed approach we combine efficient classical numerical approximation techniques such as higher-order Runge-Kutta schemes with sophisticated deep (operator) learning methodologies such as the recently introduced Fourier neural operators (FNOs). Specifically, we introduce customized adaptions of existing standard ANN architectures together with specialized initializations for these ANN architectures so that at initialization we have that the ANNs closely mimic a chosen efficient classical numerical algorithm for the considered approximation problem. The obtained ANN architectures and their initialization schemes are thus strongly inspired by numerical algorithms as well as by popular deep learning methodologies from the literature and in that sense we refer to the introduced ANNs in conjunction with their tailor-made initialization schemes as Algorithmically Designed Artificial Neural Networks (ADANNs). We numerically test the proposed ADANN approach in the case of some parametric PDEs. In the tested numerical examples the ADANN approach significantly outperforms existing traditional approximation algorithms as well as existing deep learning methodologies from the literature.

A proof that artificial neural networks overcome the curse of dimensionality in the numerical approximation of Black-Scholes partial differential equations

Artificial neural networks (ANNs) have very successfully been used in numerical simulations for a series of computational problems ranging from image classification/image recognition, speech recognition, time series analysis, game intelligence, and computational advertising to numerical approximations of partial differential equations (PDEs). Such numerical simulations suggest that ANNs have the capacity to very efficiently approximate high-dimensional functions and, especially, such numerical simulations indicate that ANNs seem to admit the fundamental power to overcome the curse of dimensionality when approximating the high-dimensional functions appearing in the above named computational problems. There are also a series of rigorous mathematical approximation results for ANNs in the scientific literature. Some of these mathematical results prove convergence without convergence rates and some of these mathematical results even rigorously establish convergence rates but there are only a few special cases where mathematical results can rigorously explain the empirical success of ANNs when approximating high-dimensional functions. The key contribution of this article is to disclose that ANNs can efficiently approximate high-dimensional functions in the case of numerical approximations of Black-Scholes PDEs. More precisely, this work reveals that the number of required parameters of an ANN to approximate the solution of the Black-Scholes PDE grows at most polynomially in both the reciprocal of the prescribed approximation accuracy $\varepsilon > 0$ and the PDE dimension $d \in \mathbb{N}$ and we thereby prove, for the first time, that ANNs do indeed overcome the curse of dimensionality in the numerical approximation of Black-Scholes PDEs.

Lower error bounds for the stochastic gradient descent optimization algorithm: Sharp convergence rates for slowly and fast decaying learning rates

The stochastic gradient descent (SGD) optimization algorithm plays a central role in a series of machine learning applications. The scientific literature provides a vast amount of upper error bounds for the SGD method. Much less attention as been paid to proving lower error bounds for the SGD method. It is the key contribution of this paper to make a step in this direction. More precisely, in this article we establish for every $\gamma, \nu \in (0,\infty)$ essentially matching lower and upper bounds for the mean square error of the SGD process with learning rates $(\frac{\gamma}{n^\nu})_{n \in \mathbb{N}}$ associated to a simple quadratic stochastic optimization problem. This allows us to precisely quantify the mean square convergence rate of the SGD method in dependence on the asymptotic behavior of the learning rates.