Benno Kuckuck
On the logical skills of large language models: evaluations using arbitrarily complex first-order logic problems
Feb 20, 2025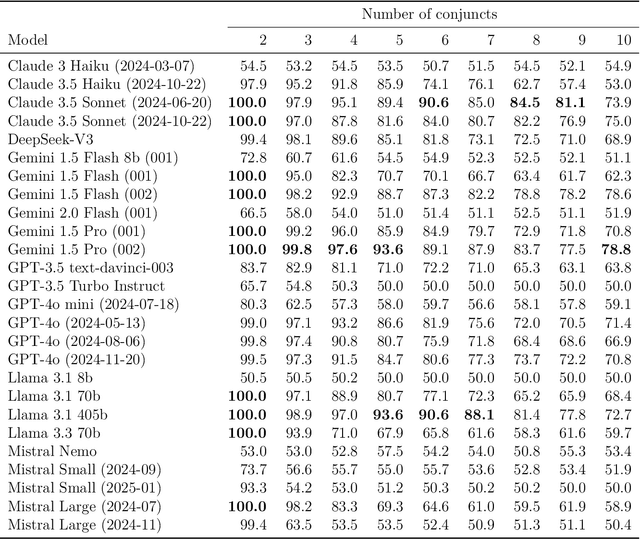
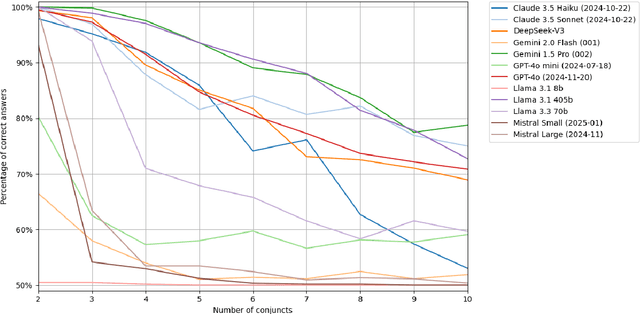
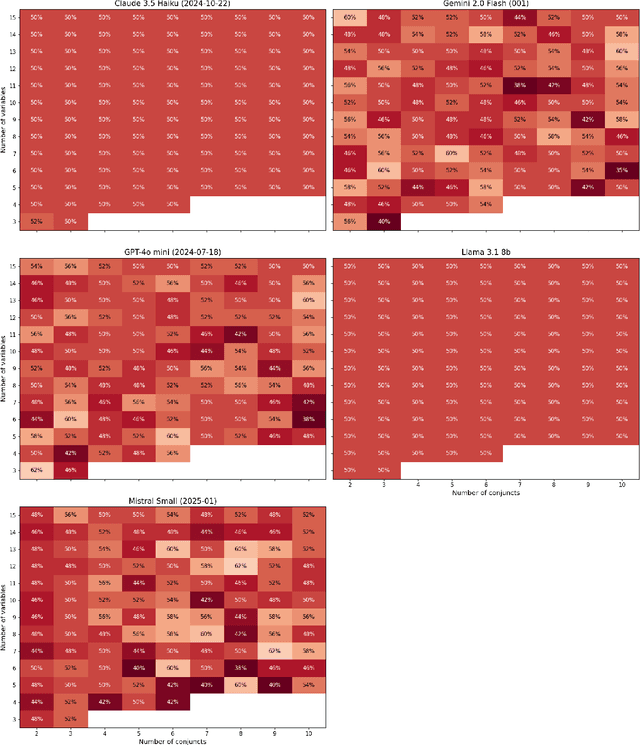
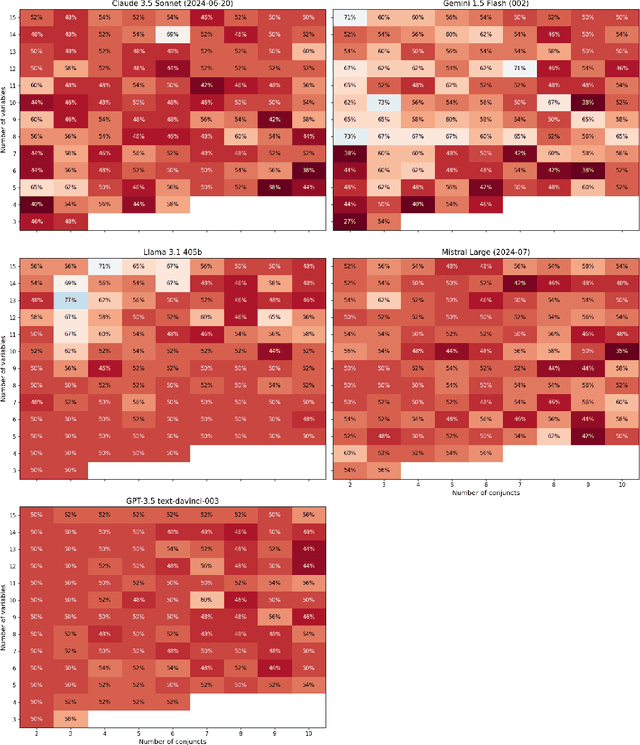
Abstract:We present a method of generating first-order logic statements whose complexity can be controlled along multiple dimensions. We use this method to automatically create several datasets consisting of questions asking for the truth or falsity of first-order logic statements in Zermelo-Fraenkel set theory. While the resolution of these questions does not require any knowledge beyond basic notation of first-order logic and set theory, it does require a degree of planning and logical reasoning, which can be controlled up to arbitrarily high difficulty by the complexity of the generated statements. Furthermore, we do extensive evaluations of the performance of various large language models, including recent models such as DeepSeek-R1 and OpenAI's o3-mini, on these datasets. All of the datasets along with the code used for generating them, as well as all data from the evaluations is publicly available at https://github.com/bkuckuck/logical-skills-of-llms.
An Overview on Machine Learning Methods for Partial Differential Equations: from Physics Informed Neural Networks to Deep Operator Learning
Aug 23, 2024



Abstract:The approximation of solutions of partial differential equations (PDEs) with numerical algorithms is a central topic in applied mathematics. For many decades, various types of methods for this purpose have been developed and extensively studied. One class of methods which has received a lot of attention in recent years are machine learning-based methods, which typically involve the training of artificial neural networks (ANNs) by means of stochastic gradient descent type optimization methods. While approximation methods for PDEs using ANNs have first been proposed in the 1990s they have only gained wide popularity in the last decade with the rise of deep learning. This article aims to provide an introduction to some of these methods and the mathematical theory on which they are based. We discuss methods such as physics-informed neural networks (PINNs) and deep BSDE methods and consider several operator learning approaches.
Mathematical Introduction to Deep Learning: Methods, Implementations, and Theory
Oct 31, 2023Abstract:This book aims to provide an introduction to the topic of deep learning algorithms. We review essential components of deep learning algorithms in full mathematical detail including different artificial neural network (ANN) architectures (such as fully-connected feedforward ANNs, convolutional ANNs, recurrent ANNs, residual ANNs, and ANNs with batch normalization) and different optimization algorithms (such as the basic stochastic gradient descent (SGD) method, accelerated methods, and adaptive methods). We also cover several theoretical aspects of deep learning algorithms such as approximation capacities of ANNs (including a calculus for ANNs), optimization theory (including Kurdyka-{\L}ojasiewicz inequalities), and generalization errors. In the last part of the book some deep learning approximation methods for PDEs are reviewed including physics-informed neural networks (PINNs) and deep Galerkin methods. We hope that this book will be useful for students and scientists who do not yet have any background in deep learning at all and would like to gain a solid foundation as well as for practitioners who would like to obtain a firmer mathematical understanding of the objects and methods considered in deep learning.
Deep neural networks with ReLU, leaky ReLU, and softplus activation provably overcome the curse of dimensionality for Kolmogorov partial differential equations with Lipschitz nonlinearities in the $L^p$-sense
Sep 24, 2023Abstract:Recently, several deep learning (DL) methods for approximating high-dimensional partial differential equations (PDEs) have been proposed. The interest that these methods have generated in the literature is in large part due to simulations which appear to demonstrate that such DL methods have the capacity to overcome the curse of dimensionality (COD) for PDEs in the sense that the number of computational operations they require to achieve a certain approximation accuracy $\varepsilon\in(0,\infty)$ grows at most polynomially in the PDE dimension $d\in\mathbb N$ and the reciprocal of $\varepsilon$. While there is thus far no mathematical result that proves that one of such methods is indeed capable of overcoming the COD, there are now a number of rigorous results in the literature that show that deep neural networks (DNNs) have the expressive power to approximate PDE solutions without the COD in the sense that the number of parameters used to describe the approximating DNN grows at most polynomially in both the PDE dimension $d\in\mathbb N$ and the reciprocal of the approximation accuracy $\varepsilon>0$. Roughly speaking, in the literature it is has been proved for every $T>0$ that solutions $u_d\colon [0,T]\times\mathbb R^d\to \mathbb R$, $d\in\mathbb N$, of semilinear heat PDEs with Lipschitz continuous nonlinearities can be approximated by DNNs with ReLU activation at the terminal time in the $L^2$-sense without the COD provided that the initial value functions $\mathbb R^d\ni x\mapsto u_d(0,x)\in\mathbb R$, $d\in\mathbb N$, can be approximated by ReLU DNNs without the COD. It is the key contribution of this work to generalize this result by establishing this statement in the $L^p$-sense with $p\in(0,\infty)$ and by allowing the activation function to be more general covering the ReLU, the leaky ReLU, and the softplus activation functions as special cases.
Deep learning approximations for non-local nonlinear PDEs with Neumann boundary conditions
May 07, 2022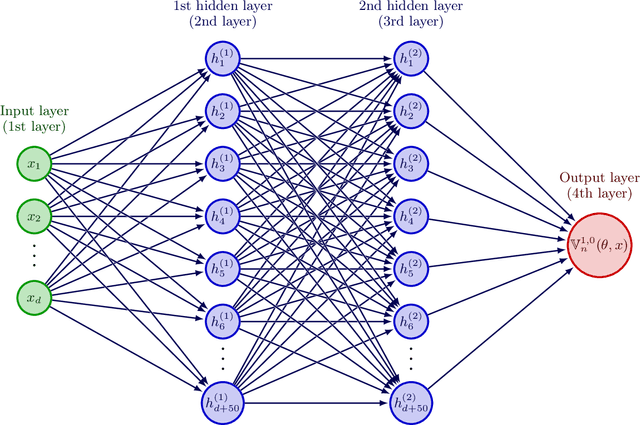
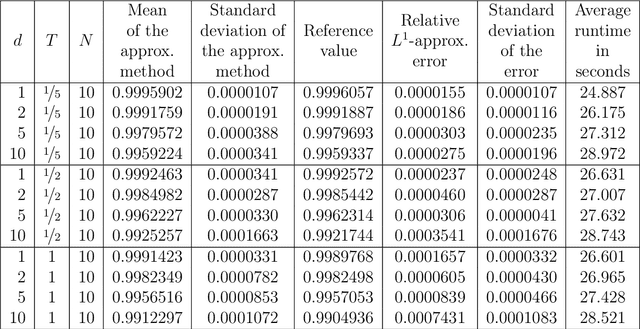
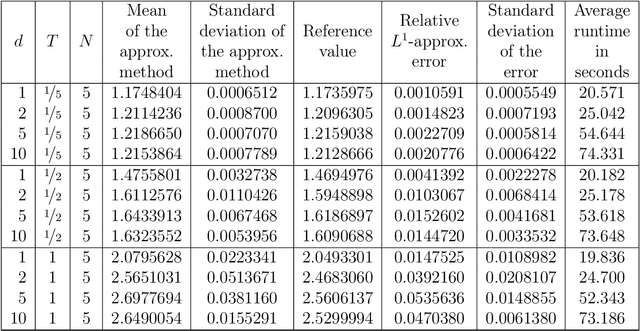
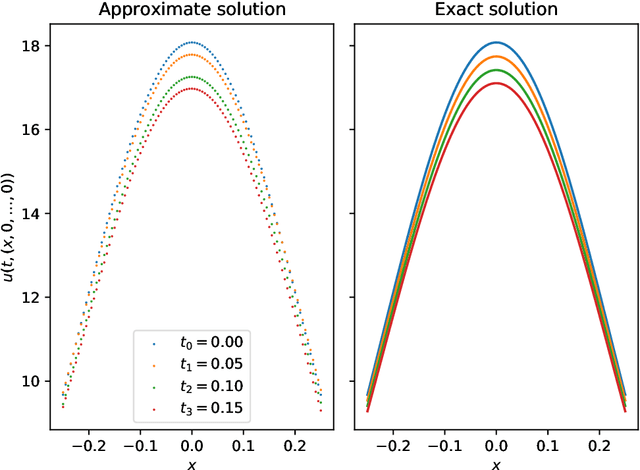
Abstract:Nonlinear partial differential equations (PDEs) are used to model dynamical processes in a large number of scientific fields, ranging from finance to biology. In many applications standard local models are not sufficient to accurately account for certain non-local phenomena such as, e.g., interactions at a distance. In order to properly capture these phenomena non-local nonlinear PDE models are frequently employed in the literature. In this article we propose two numerical methods based on machine learning and on Picard iterations, respectively, to approximately solve non-local nonlinear PDEs. The proposed machine learning-based method is an extended variant of a deep learning-based splitting-up type approximation method previously introduced in the literature and utilizes neural networks to provide approximate solutions on a subset of the spatial domain of the solution. The Picard iterations-based method is an extended variant of the so-called full history recursive multilevel Picard approximation scheme previously introduced in the literature and provides an approximate solution for a single point of the domain. Both methods are mesh-free and allow non-local nonlinear PDEs with Neumann boundary conditions to be solved in high dimensions. In the two methods, the numerical difficulties arising due to the dimensionality of the PDEs are avoided by (i) using the correspondence between the expected trajectory of reflected stochastic processes and the solution of PDEs (given by the Feynman-Kac formula) and by (ii) using a plain vanilla Monte Carlo integration to handle the non-local term. We evaluate the performance of the two methods on five different PDEs arising in physics and biology. In all cases, the methods yield good results in up to 10 dimensions with short run times. Our work extends recently developed methods to overcome the curse of dimensionality in solving PDEs.
An overview on deep learning-based approximation methods for partial differential equations
Dec 22, 2020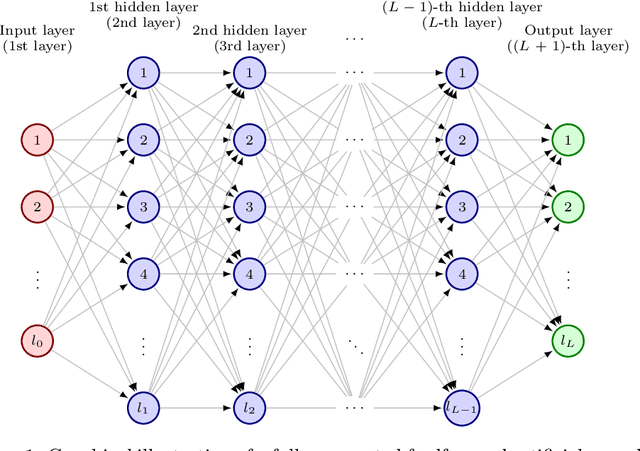
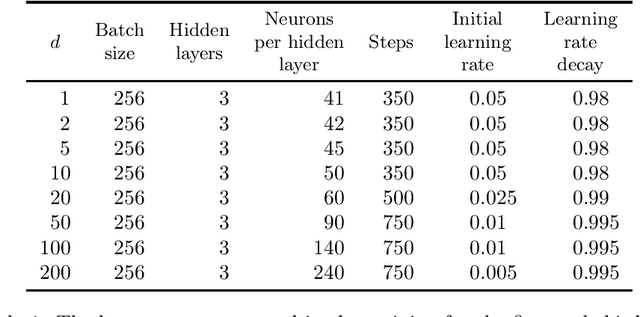
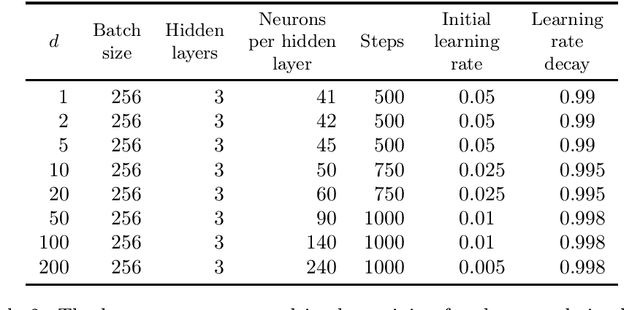
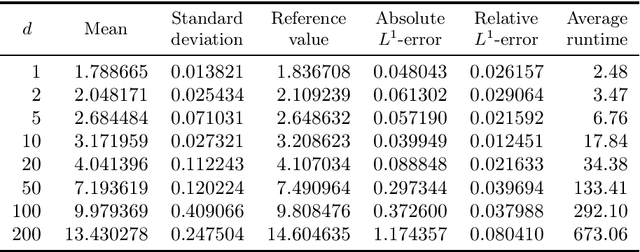
Abstract:It is one of the most challenging problems in applied mathematics to approximatively solve high-dimensional partial differential equations (PDEs). Recently, several deep learning-based approximation algorithms for attacking this problem have been proposed and tested numerically on a number of examples of high-dimensional PDEs. This has given rise to a lively field of research in which deep learning-based methods and related Monte Carlo methods are applied to the approximation of high-dimensional PDEs. In this article we offer an introduction to this field of research, we review some of the main ideas of deep learning-based approximation methods for PDEs, we revisit one of the central mathematical results for deep neural network approximations for PDEs, and we provide an overview of the recent literature in this area of research.
Full error analysis for the training of deep neural networks
Sep 30, 2019Abstract:Deep learning algorithms have been applied very successfully in recent years to a range of problems out of reach for classical solution paradigms. Nevertheless, there is no completely rigorous mathematical error and convergence analysis which explains the success of deep learning algorithms. The error of a deep learning algorithm can in many situations be decomposed into three parts, the approximation error, the generalization error, and the optimization error. In this work we estimate for a certain deep learning algorithm each of these three errors and combine these three error estimates to obtain an overall error analysis for the deep learning algorithm under consideration. In particular, we thereby establish convergence with a suitable convergence speed for the overall error of the deep learning algorithm under consideration. Our convergence speed analysis is far from optimal and the convergence speed that we establish is rather slow, increases exponentially in the dimensions, and, in particular, suffers from the curse of dimensionality. The main contribution of this work is, instead, to provide a full error analysis (i) which covers each of the three different sources of errors usually emerging in deep learning algorithms and (ii) which merges these three sources of errors into one overall error estimate for the considered deep learning algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge