An overview on deep learning-based approximation methods for partial differential equations

It is one of the most challenging problems in applied mathematics to approximatively solve high-dimensional partial differential equations (PDEs). Recently, several deep learning-based approximation algorithms for attacking this problem have been proposed and tested numerically on a number of examples of high-dimensional PDEs. This has given rise to a lively field of research in which deep learning-based methods and related Monte Carlo methods are applied to the approximation of high-dimensional PDEs. In this article we offer an introduction to this field of research, we review some of the main ideas of deep learning-based approximation methods for PDEs, we revisit one of the central mathematical results for deep neural network approximations for PDEs, and we provide an overview of the recent literature in this area of research.

Deep learning based numerical approximation algorithms for stochastic partial differential equations and high-dimensional nonlinear filtering problems

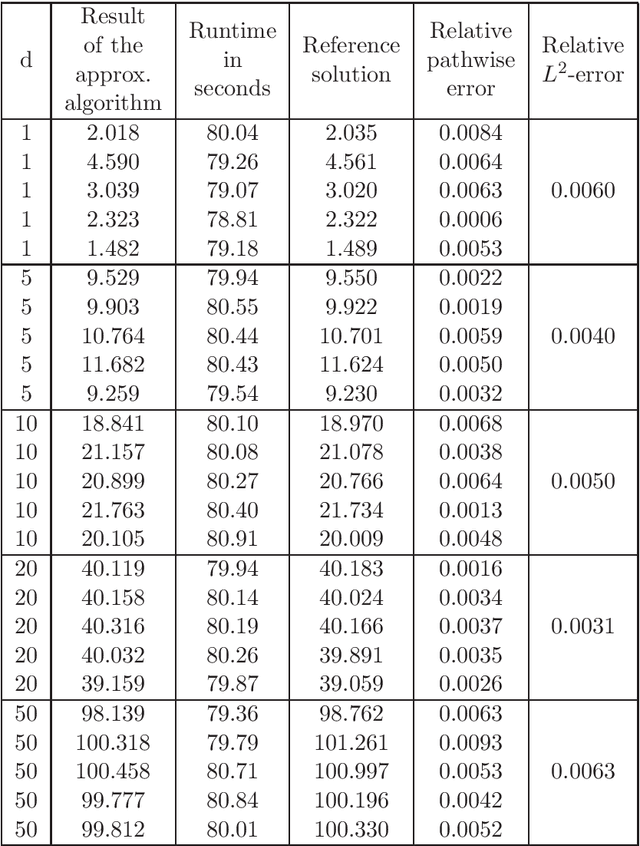
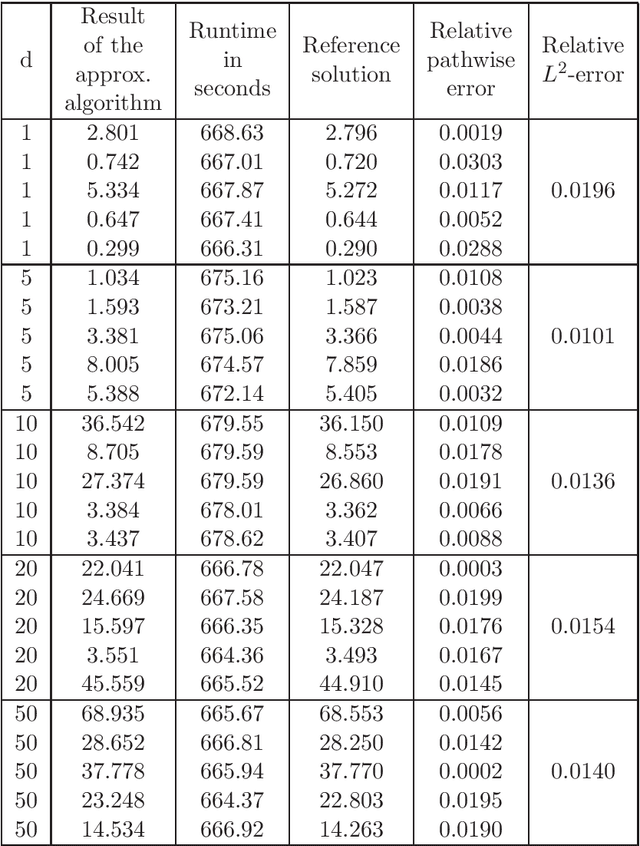
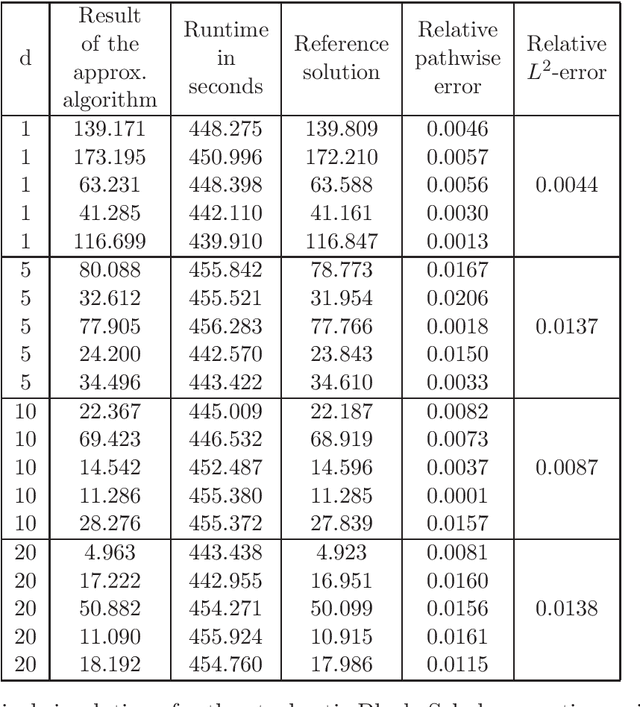
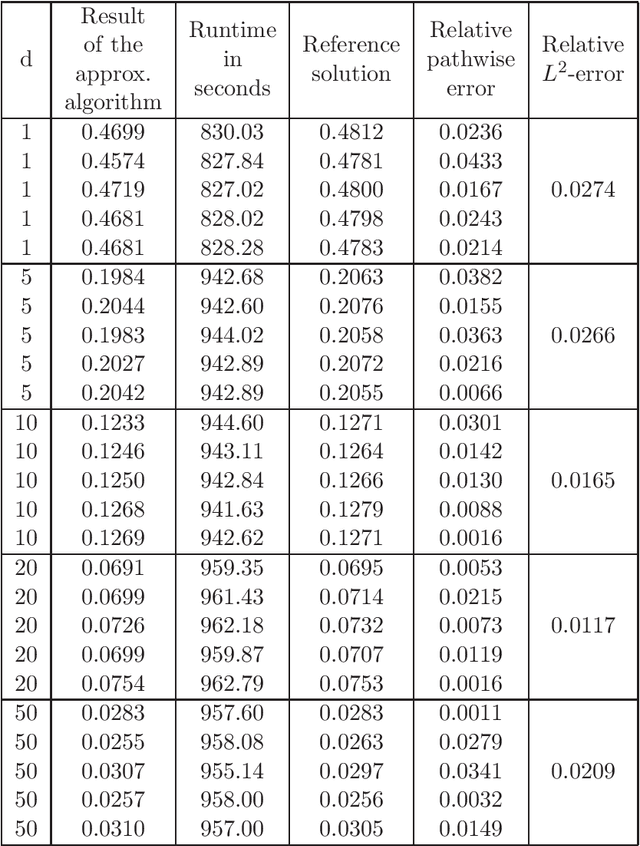
In this article we introduce and study a deep learning based approximation algorithm for solutions of stochastic partial differential equations (SPDEs). In the proposed approximation algorithm we employ a deep neural network for every realization of the driving noise process of the SPDE to approximate the solution process of the SPDE under consideration. We test the performance of the proposed approximation algorithm in the case of stochastic heat equations with additive noise, stochastic heat equations with multiplicative noise, stochastic Black--Scholes equations with multiplicative noise, and Zakai equations from nonlinear filtering. In each of these SPDEs the proposed approximation algorithm produces accurate results with short run times in up to 50 space dimensions.

Deep splitting method for parabolic PDEs

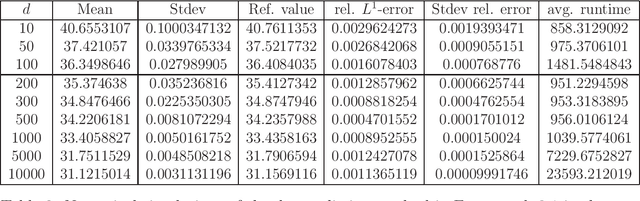
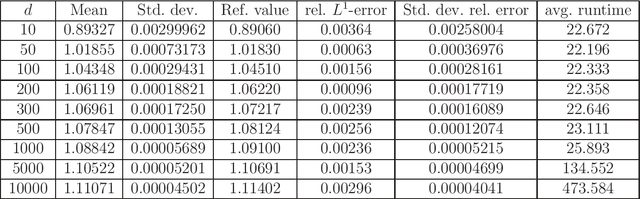
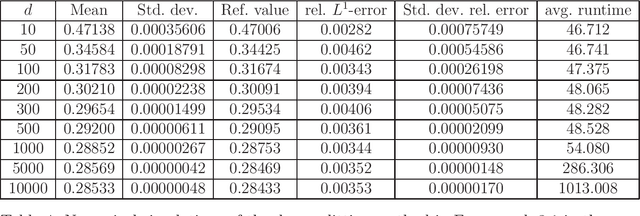
In this paper we introduce a numerical method for parabolic PDEs that combines operator splitting with deep learning. It divides the PDE approximation problem into a sequence of separate learning problems. Since the computational graph for each of the subproblems is comparatively small, the approach can handle extremely high-dimensional PDEs. We test the method on different examples from physics, stochastic control, and mathematical finance. In all cases, it yields very good results in up to 10,000 dimensions with short run times.

Solving stochastic differential equations and Kolmogorov equations by means of deep learning

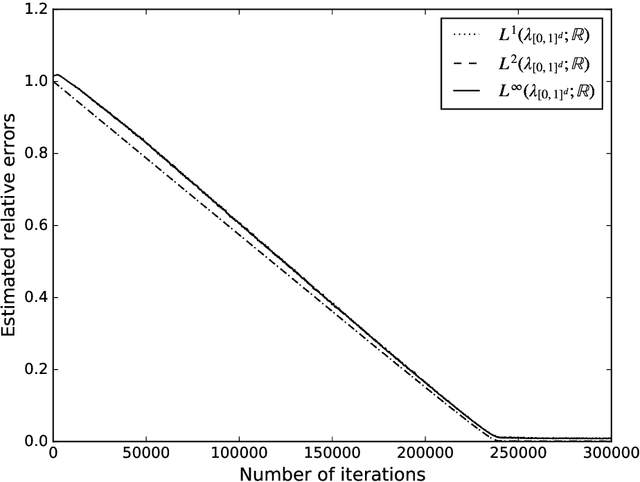
Stochastic differential equations (SDEs) and the Kolmogorov partial differential equations (PDEs) associated to them have been widely used in models from engineering, finance, and the natural sciences. In particular, SDEs and Kolmogorov PDEs, respectively, are highly employed in models for the approximative pricing of financial derivatives. Kolmogorov PDEs and SDEs, respectively, can typically not be solved explicitly and it has been and still is an active topic of research to design and analyze numerical methods which are able to approximately solve Kolmogorov PDEs and SDEs, respectively. Nearly all approximation methods for Kolmogorov PDEs in the literature suffer under the curse of dimensionality or only provide approximations of the solution of the PDE at a single fixed space-time point. In this paper we derive and propose a numerical approximation method which aims to overcome both of the above mentioned drawbacks and intends to deliver a numerical approximation of the Kolmogorov PDE on an entire region $[a,b]^d$ without suffering from the curse of dimensionality. Numerical results on examples including the heat equation, the Black-Scholes model, the stochastic Lorenz equation, and the Heston model suggest that the proposed approximation algorithm is quite effective in high dimensions in terms of both accuracy and speed.

Machine learning approximation algorithms for high-dimensional fully nonlinear partial differential equations and second-order backward stochastic differential equations

High-dimensional partial differential equations (PDE) appear in a number of models from the financial industry, such as in derivative pricing models, credit valuation adjustment (CVA) models, or portfolio optimization models. The PDEs in such applications are high-dimensional as the dimension corresponds to the number of financial assets in a portfolio. Moreover, such PDEs are often fully nonlinear due to the need to incorporate certain nonlinear phenomena in the model such as default risks, transaction costs, volatility uncertainty (Knightian uncertainty), or trading constraints in the model. Such high-dimensional fully nonlinear PDEs are exceedingly difficult to solve as the computational effort for standard approximation methods grows exponentially with the dimension. In this work we propose a new method for solving high-dimensional fully nonlinear second-order PDEs. Our method can in particular be used to sample from high-dimensional nonlinear expectations. The method is based on (i) a connection between fully nonlinear second-order PDEs and second-order backward stochastic differential equations (2BSDEs), (ii) a merged formulation of the PDE and the 2BSDE problem, (iii) a temporal forward discretization of the 2BSDE and a spatial approximation via deep neural nets, and (iv) a stochastic gradient descent-type optimization procedure. Numerical results obtained using ${\rm T{\small ENSOR}F{\small LOW}}$ in ${\rm P{\small YTHON}}$ illustrate the efficiency and the accuracy of the method in the cases of a $100$-dimensional Black-Scholes-Barenblatt equation, a $100$-dimensional Hamilton-Jacobi-Bellman equation, and a nonlinear expectation of a $ 100 $-dimensional $ G $-Brownian motion.