Deep learning based numerical approximation algorithms for stochastic partial differential equations and high-dimensional nonlinear filtering problems
Paper and Code
Dec 02, 2020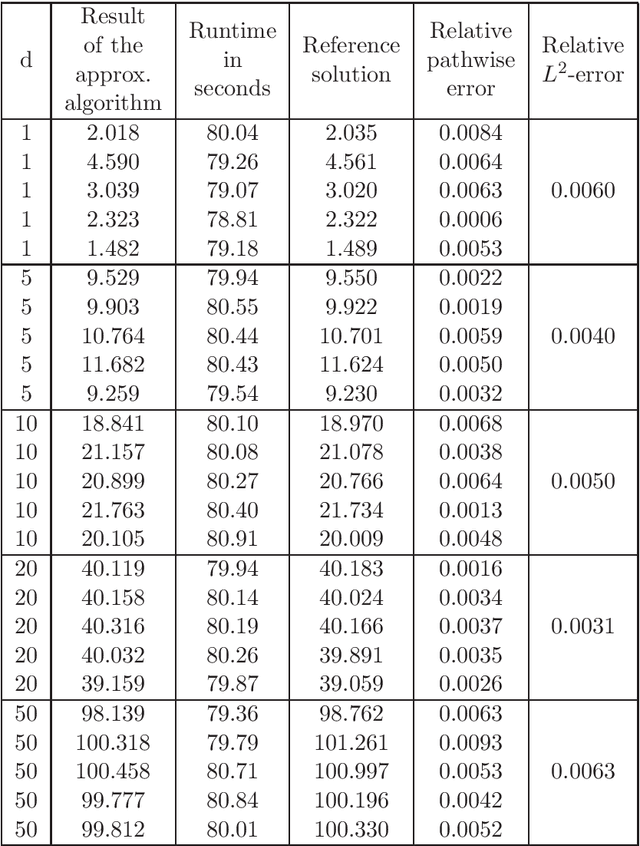
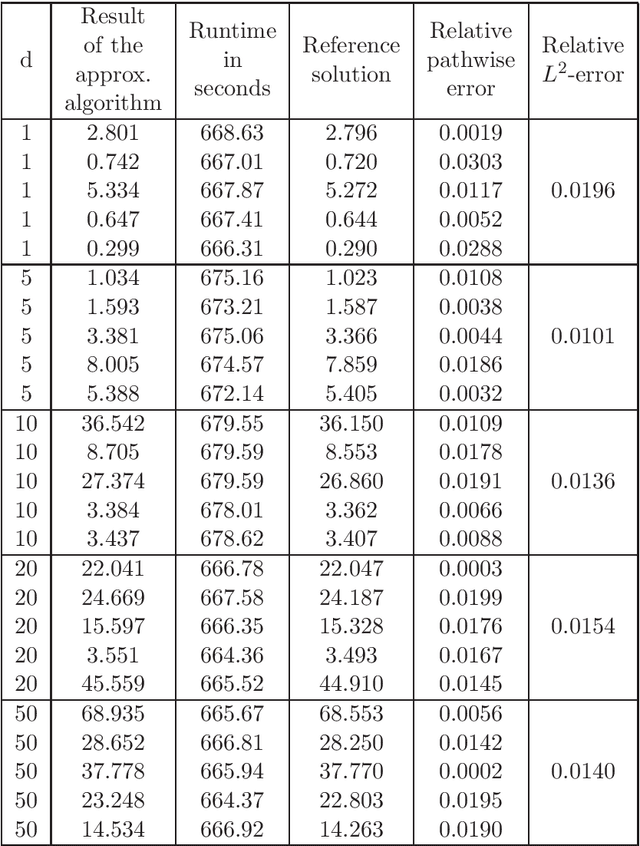
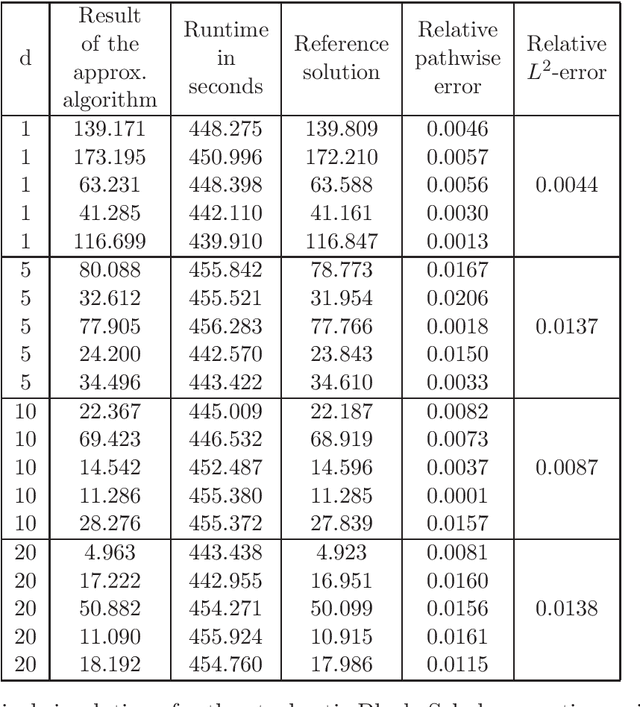
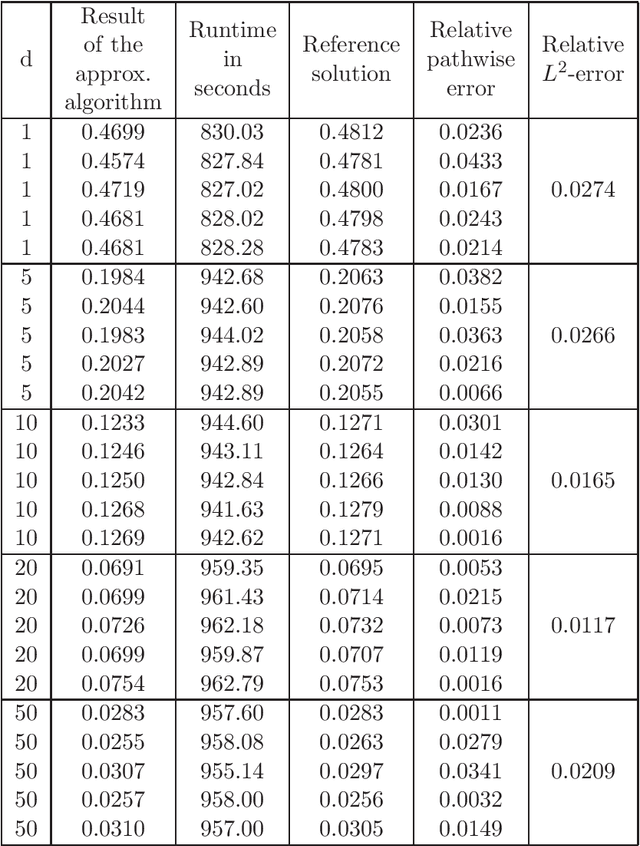
In this article we introduce and study a deep learning based approximation algorithm for solutions of stochastic partial differential equations (SPDEs). In the proposed approximation algorithm we employ a deep neural network for every realization of the driving noise process of the SPDE to approximate the solution process of the SPDE under consideration. We test the performance of the proposed approximation algorithm in the case of stochastic heat equations with additive noise, stochastic heat equations with multiplicative noise, stochastic Black--Scholes equations with multiplicative noise, and Zakai equations from nonlinear filtering. In each of these SPDEs the proposed approximation algorithm produces accurate results with short run times in up to 50 space dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge