Deep learning approximations for non-local nonlinear PDEs with Neumann boundary conditions

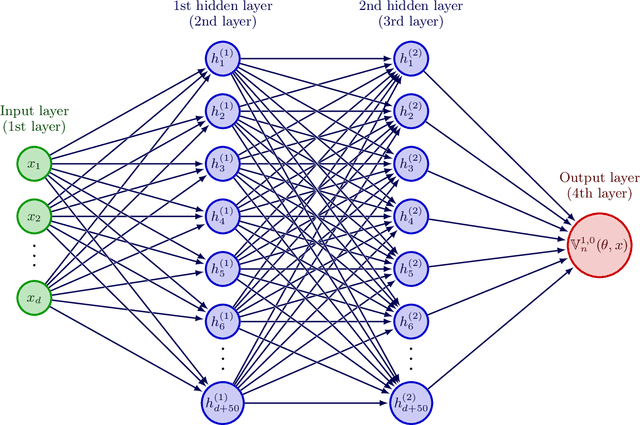
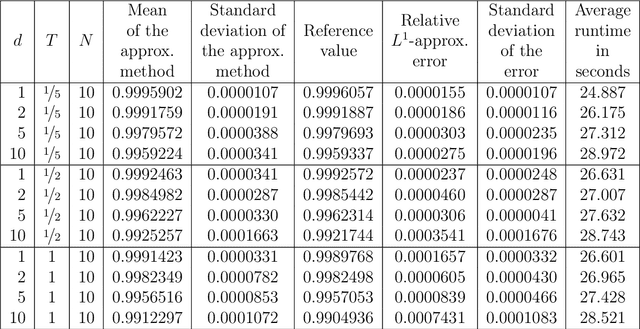
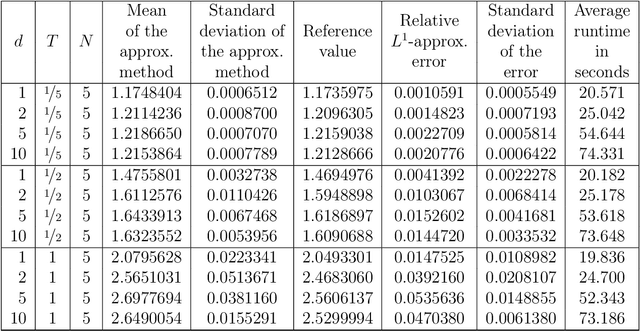
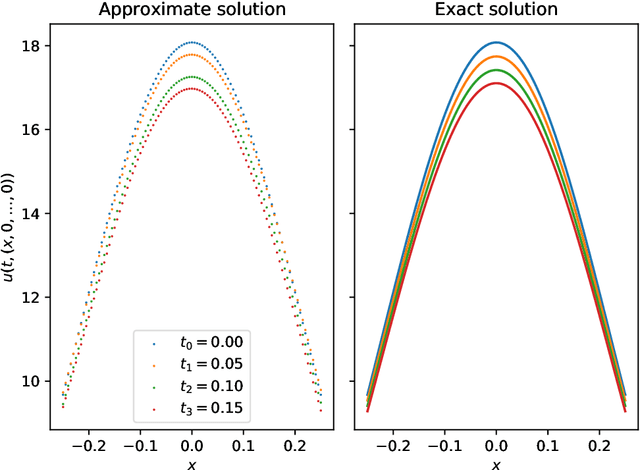
Nonlinear partial differential equations (PDEs) are used to model dynamical processes in a large number of scientific fields, ranging from finance to biology. In many applications standard local models are not sufficient to accurately account for certain non-local phenomena such as, e.g., interactions at a distance. In order to properly capture these phenomena non-local nonlinear PDE models are frequently employed in the literature. In this article we propose two numerical methods based on machine learning and on Picard iterations, respectively, to approximately solve non-local nonlinear PDEs. The proposed machine learning-based method is an extended variant of a deep learning-based splitting-up type approximation method previously introduced in the literature and utilizes neural networks to provide approximate solutions on a subset of the spatial domain of the solution. The Picard iterations-based method is an extended variant of the so-called full history recursive multilevel Picard approximation scheme previously introduced in the literature and provides an approximate solution for a single point of the domain. Both methods are mesh-free and allow non-local nonlinear PDEs with Neumann boundary conditions to be solved in high dimensions. In the two methods, the numerical difficulties arising due to the dimensionality of the PDEs are avoided by (i) using the correspondence between the expected trajectory of reflected stochastic processes and the solution of PDEs (given by the Feynman-Kac formula) and by (ii) using a plain vanilla Monte Carlo integration to handle the non-local term. We evaluate the performance of the two methods on five different PDEs arising in physics and biology. In all cases, the methods yield good results in up to 10 dimensions with short run times. Our work extends recently developed methods to overcome the curse of dimensionality in solving PDEs.

Deep learning based numerical approximation algorithms for stochastic partial differential equations and high-dimensional nonlinear filtering problems

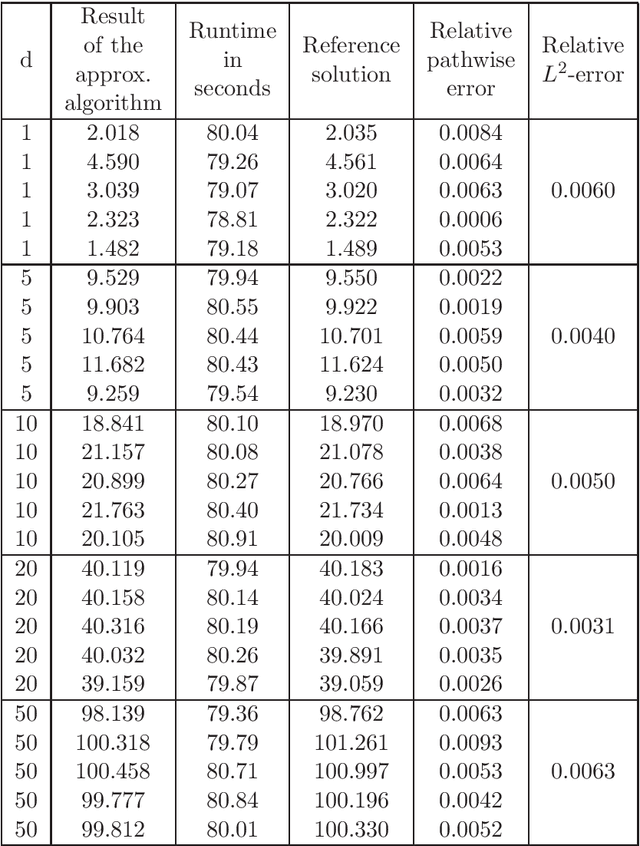
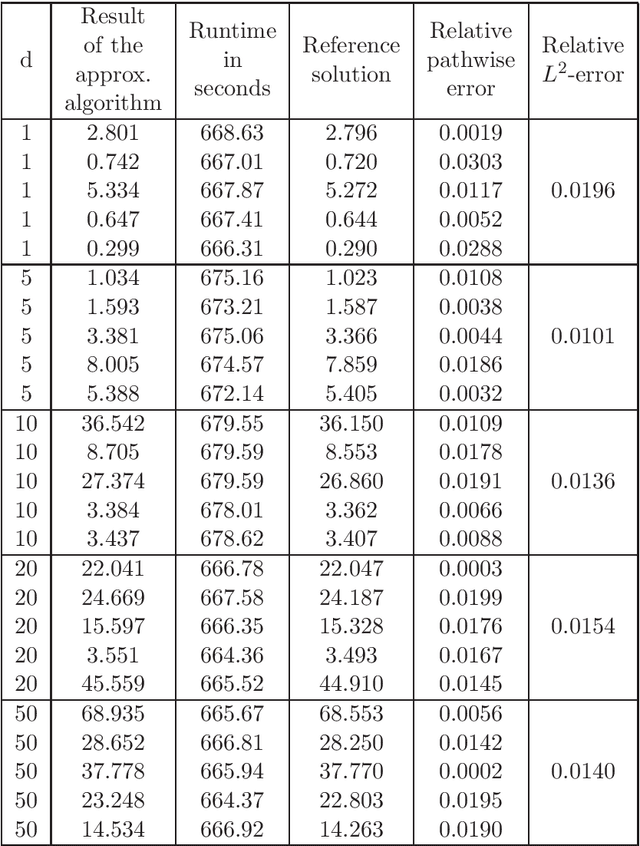
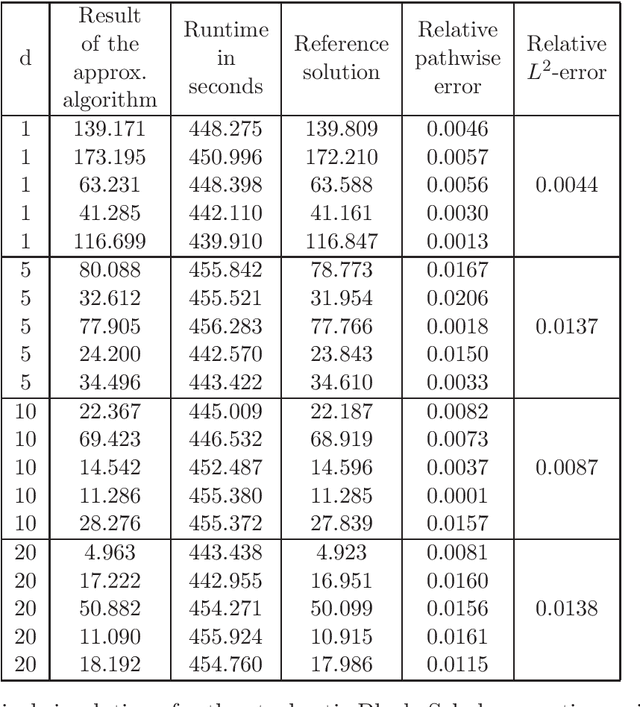
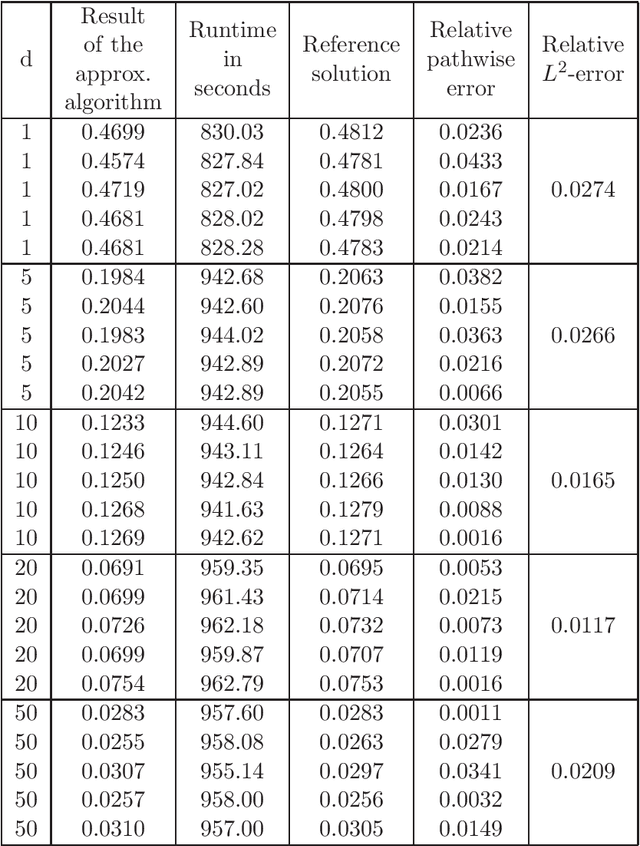
In this article we introduce and study a deep learning based approximation algorithm for solutions of stochastic partial differential equations (SPDEs). In the proposed approximation algorithm we employ a deep neural network for every realization of the driving noise process of the SPDE to approximate the solution process of the SPDE under consideration. We test the performance of the proposed approximation algorithm in the case of stochastic heat equations with additive noise, stochastic heat equations with multiplicative noise, stochastic Black--Scholes equations with multiplicative noise, and Zakai equations from nonlinear filtering. In each of these SPDEs the proposed approximation algorithm produces accurate results with short run times in up to 50 space dimensions.

Solving high-dimensional optimal stopping problems using deep learning

Nowadays many financial derivatives which are traded on stock and futures exchanges, such as American or Bermudan options, are of early exercise type. Often the pricing of early exercise options gives rise to high-dimensional optimal stopping problems, since the dimension corresponds to the number of underlyings in the associated hedging portfolio. High-dimensional optimal stopping problems are, however, notoriously difficult to solve due to the well-known curse of dimensionality. In this work we propose an algorithm for solving such problems, which is based on deep learning and computes, in the context of early exercise option pricing, both approximations for an optimal exercise strategy and the price of the considered option. The proposed algorithm can also be applied to optimal stopping problems that arise in other areas where the underlying stochastic process can be efficiently simulated. We present numerical results for a large number of example problems, which include the pricing of many high-dimensional American and Bermudan options such as, for example, Bermudan max-call options in up to 5000 dimensions. Most of the obtained results are compared to reference values computed by exploiting the specific problem design or, where available, to reference values from the literature. These numerical results suggest that the proposed algorithm is highly effective in the case of many underlyings, in terms of both accuracy and speed.

Deep splitting method for parabolic PDEs

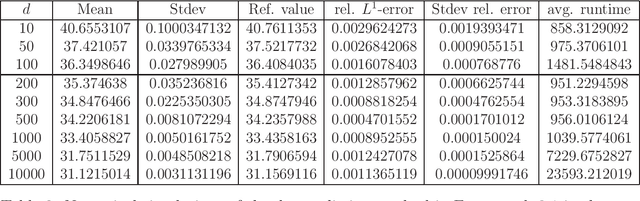
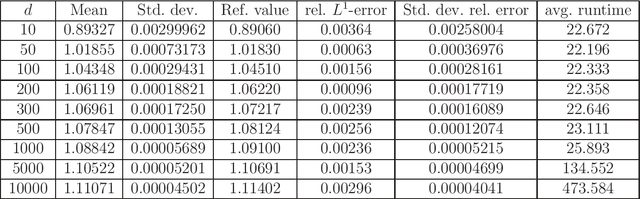
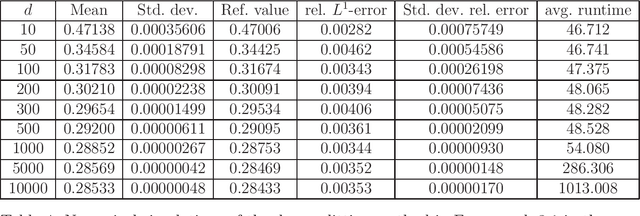
In this paper we introduce a numerical method for parabolic PDEs that combines operator splitting with deep learning. It divides the PDE approximation problem into a sequence of separate learning problems. Since the computational graph for each of the subproblems is comparatively small, the approach can handle extremely high-dimensional PDEs. We test the method on different examples from physics, stochastic control, and mathematical finance. In all cases, it yields very good results in up to 10,000 dimensions with short run times.

Solving stochastic differential equations and Kolmogorov equations by means of deep learning

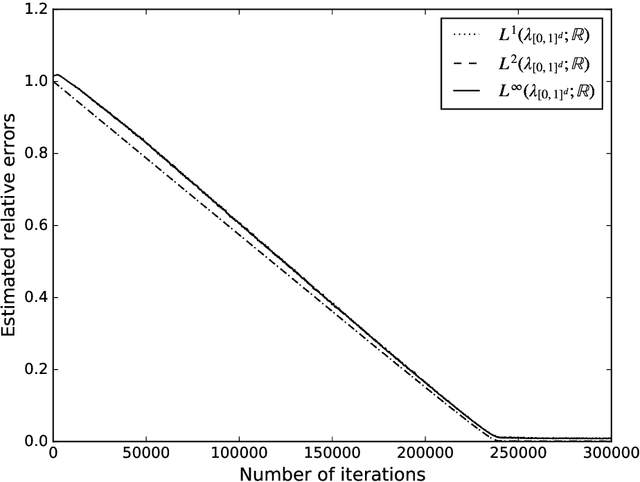
Stochastic differential equations (SDEs) and the Kolmogorov partial differential equations (PDEs) associated to them have been widely used in models from engineering, finance, and the natural sciences. In particular, SDEs and Kolmogorov PDEs, respectively, are highly employed in models for the approximative pricing of financial derivatives. Kolmogorov PDEs and SDEs, respectively, can typically not be solved explicitly and it has been and still is an active topic of research to design and analyze numerical methods which are able to approximately solve Kolmogorov PDEs and SDEs, respectively. Nearly all approximation methods for Kolmogorov PDEs in the literature suffer under the curse of dimensionality or only provide approximations of the solution of the PDE at a single fixed space-time point. In this paper we derive and propose a numerical approximation method which aims to overcome both of the above mentioned drawbacks and intends to deliver a numerical approximation of the Kolmogorov PDE on an entire region $[a,b]^d$ without suffering from the curse of dimensionality. Numerical results on examples including the heat equation, the Black-Scholes model, the stochastic Lorenz equation, and the Heston model suggest that the proposed approximation algorithm is quite effective in high dimensions in terms of both accuracy and speed.