QuLTSF: Long-Term Time Series Forecasting with Quantum Machine Learning

Long-term time series forecasting (LTSF) involves predicting a large number of future values of a time series based on the past values and is an essential task in a wide range of domains including weather forecasting, stock market analysis, disease outbreak prediction. Over the decades LTSF algorithms have transitioned from statistical models to deep learning models like transformer models. Despite the complex architecture of transformer based LTSF models `Are Transformers Effective for Time Series Forecasting? (Zeng et al., 2023)' showed that simple linear models can outperform the state-of-the-art transformer based LTSF models. Recently, quantum machine learning (QML) is evolving as a domain to enhance the capabilities of classical machine learning models. In this paper we initiate the application of QML to LTSF problems by proposing QuLTSF, a simple hybrid QML model for multivariate LTSF. Through extensive experiments on a widely used weather dataset we show the advantages of QuLTSF over the state-of-the-art classical linear models, in terms of reduced mean squared error and mean absolute error.

Solving stochastic partial differential equations using neural networks in the Wiener chaos expansion

In this paper, we solve stochastic partial differential equations (SPDEs) numerically by using (possibly random) neural networks in the truncated Wiener chaos expansion of their corresponding solution. Moreover, we provide some approximation rates for learning the solution of SPDEs with additive and/or multiplicative noise. Finally, we apply our results in numerical examples to approximate the solution of three SPDEs: the stochastic heat equation, the Heath-Jarrow-Morton equation, and the Zakai equation.

Universal approximation results for neural networks with non-polynomial activation function over non-compact domains

In this paper, we generalize the universal approximation property of single-hidden-layer feed-forward neural networks beyond the classical formulation over compact domains. More precisely, by assuming that the activation function is non-polynomial, we derive universal approximation results for neural networks within function spaces over non-compact subsets of a Euclidean space, e.g., weighted spaces, $L^p$-spaces, and (weighted) Sobolev spaces over unbounded domains, where the latter includes the approximation of the (weak) derivatives. Furthermore, we provide some dimension-independent rates for approximating a function with sufficiently regular and integrable Fourier transform by neural networks with non-polynomial activation function.

Multilevel Picard approximations and deep neural networks with ReLU, leaky ReLU, and softplus activation overcome the curse of dimensionality when approximating semilinear parabolic partial differential equations in $L^p$-sense

We prove that multilevel Picard approximations and deep neural networks with ReLU, leaky ReLU, and softplus activation are capable of approximating solutions of semilinear Kolmogorov PDEs in $L^\mathfrak{p}$-sense, $\mathfrak{p}\in [2,\infty)$, in the case of gradient-independent, Lipschitz-continuous nonlinearities, while the computational effort of the multilevel Picard approximations and the required number of parameters in the neural networks grow at most polynomially in both dimension $d\in \mathbb{N}$ and reciprocal of the prescribed accuracy $\epsilon$.

Non-asymptotic convergence analysis of the stochastic gradient Hamiltonian Monte Carlo algorithm with discontinuous stochastic gradient with applications to training of ReLU neural networks

In this paper, we provide a non-asymptotic analysis of the convergence of the stochastic gradient Hamiltonian Monte Carlo (SGHMC) algorithm to a target measure in Wasserstein-1 and Wasserstein-2 distance. Crucially, compared to the existing literature on SGHMC, we allow its stochastic gradient to be discontinuous. This allows us to provide explicit upper bounds, which can be controlled to be arbitrarily small, for the expected excess risk of non-convex stochastic optimization problems with discontinuous stochastic gradients, including, among others, the training of neural networks with ReLU activation function. To illustrate the applicability of our main results, we consider numerical experiments on quantile estimation and on several optimization problems involving ReLU neural networks relevant in finance and artificial intelligence.

Non-asymptotic estimates for accelerated high order Langevin Monte Carlo algorithms

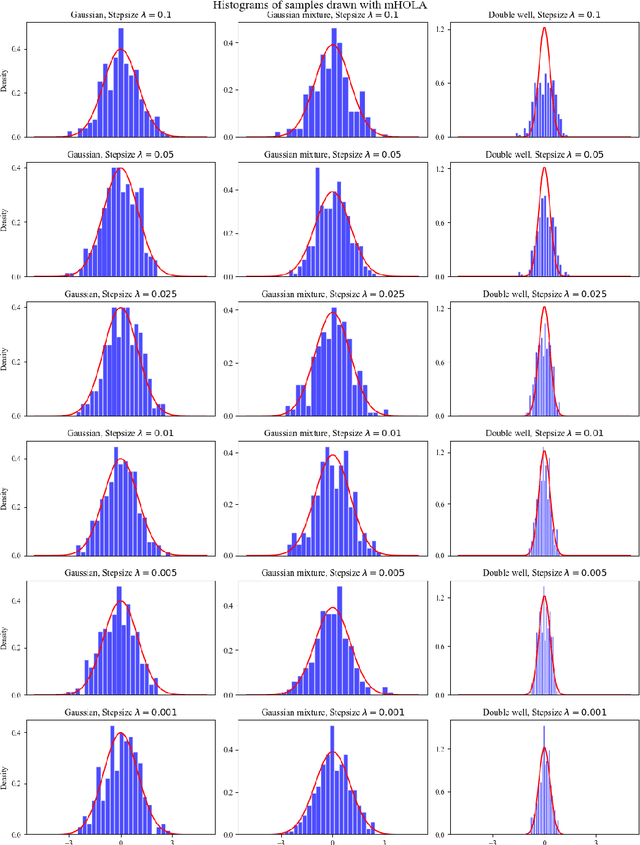
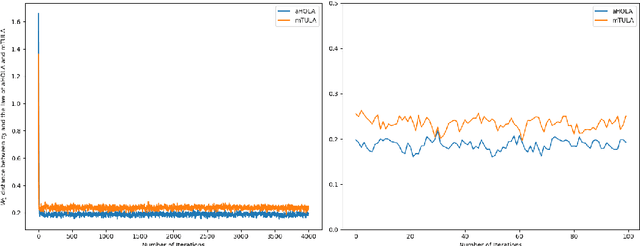
In this paper, we propose two new algorithms, namely aHOLA and aHOLLA, to sample from high-dimensional target distributions with possibly super-linearly growing potentials. We establish non-asymptotic convergence bounds for aHOLA in Wasserstein-1 and Wasserstein-2 distances with rates of convergence equal to $1+q/2$ and $1/2+q/4$, respectively, under a local H\"{o}lder condition with exponent $q\in(0,1]$ and a convexity at infinity condition on the potential of the target distribution. Similar results are obtained for aHOLLA under certain global continuity conditions and a dissipativity condition. Crucially, we achieve state-of-the-art rates of convergence of the proposed algorithms in the non-convex setting which are higher than those of the existing algorithms. Numerical experiments are conducted to sample from several distributions and the results support our main findings.

Full error analysis of the random deep splitting method for nonlinear parabolic PDEs and PIDEs with infinite activity

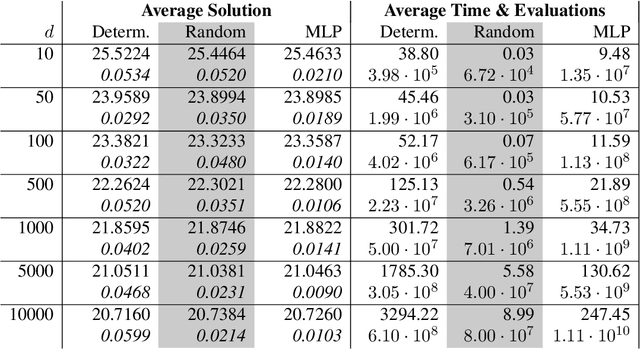
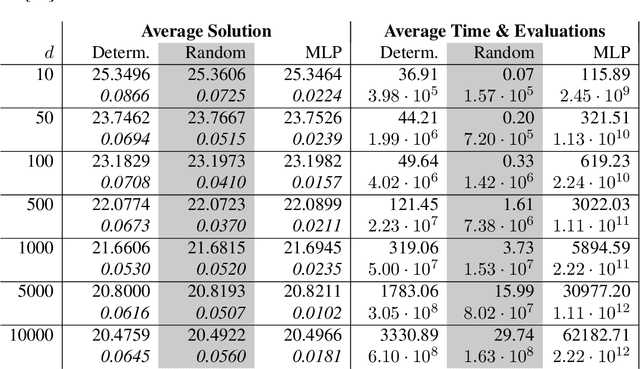
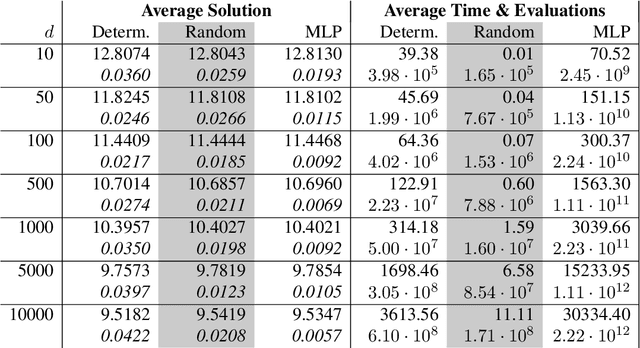
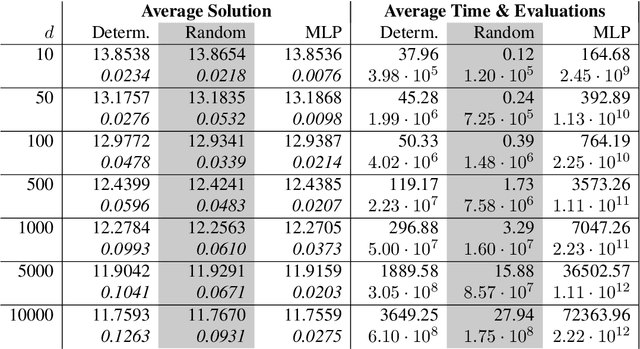
In this paper, we present a randomized extension of the deep splitting algorithm introduced in [Beck, Becker, Cheridito, Jentzen, and Neufeld (2021)] using random neural networks suitable to approximately solve both high-dimensional nonlinear parabolic PDEs and PIDEs with jumps having (possibly) infinite activity. We provide a full error analysis of our so-called random deep splitting method. In particular, we prove that our random deep splitting method converges to the (unique viscosity) solution of the nonlinear PDE or PIDE under consideration. Moreover, we empirically analyze our random deep splitting method by considering several numerical examples including both nonlinear PDEs and nonlinear PIDEs relevant in the context of pricing of financial derivatives under default risk. In particular, we empirically demonstrate in all examples that our random deep splitting method can approximately solve nonlinear PDEs and PIDEs in 10'000 dimensions within seconds.

Universal Approximation Property of Random Neural Networks

In this paper, we study random neural networks which are single-hidden-layer feedforward neural networks whose weights and biases are randomly initialized. After this random initialization, only the linear readout needs to be trained, which can be performed efficiently, e.g., by the least squares method. By viewing random neural networks as Banach space-valued random variables, we prove a universal approximation theorem within a large class of Bochner spaces. Hereby, the corresponding Banach space can be significantly more general than the space of continuous functions over a compact subset of a Euclidean space, namely, e.g., an $L^p$-space or a Sobolev space, where the latter includes the approximation of the derivatives. Moreover, we derive approximation rates and an explicit algorithm to learn a deterministic function by a random neural network. In addition, we provide a full error analysis and study when random neural networks overcome the curse of dimensionality in the sense that the training costs scale at most polynomially in the input and output dimension. Furthermore, we show in two numerical examples the empirical advantages of random neural networks compared to fully trained deterministic neural networks.

Neural networks can detect model-free static arbitrage strategies

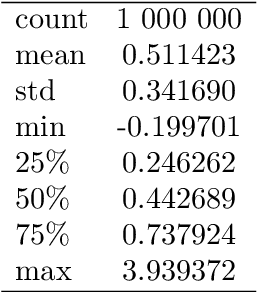
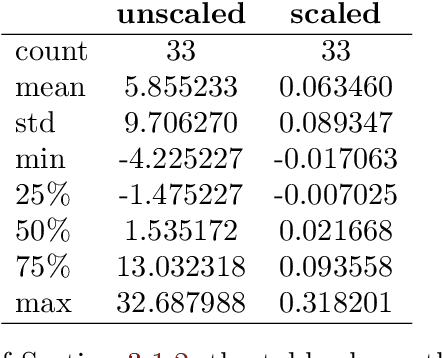
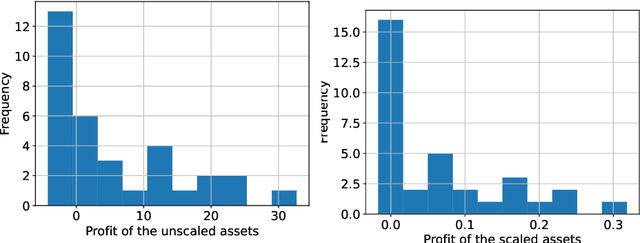
In this paper we demonstrate both theoretically as well as numerically that neural networks can detect model-free static arbitrage opportunities whenever the market admits some. Due to the use of neural networks, our method can be applied to financial markets with a high number of traded securities and ensures almost immediate execution of the corresponding trading strategies. To demonstrate its tractability, effectiveness, and robustness we provide examples using real financial data. From a technical point of view, we prove that a single neural network can approximately solve a class of convex semi-infinite programs, which is the key result in order to derive our theoretical results that neural networks can detect model-free static arbitrage strategies whenever the financial market admits such opportunities.

Langevin dynamics based algorithm e-TH$\varepsilon$O POULA for stochastic optimization problems with discontinuous stochastic gradient

We introduce a new Langevin dynamics based algorithm, called e-TH$\varepsilon$O POULA, to solve optimization problems with discontinuous stochastic gradients which naturally appear in real-world applications such as quantile estimation, vector quantization, CVaR minimization, and regularized optimization problems involving ReLU neural networks. We demonstrate both theoretically and numerically the applicability of the e-TH$\varepsilon$O POULA algorithm. More precisely, under the conditions that the stochastic gradient is locally Lipschitz in average and satisfies a certain convexity at infinity condition, we establish non-asymptotic error bounds for e-TH$\varepsilon$O POULA in Wasserstein distances and provide a non-asymptotic estimate for the expected excess risk, which can be controlled to be arbitrarily small. Three key applications in finance and insurance are provided, namely, multi-period portfolio optimization, transfer learning in multi-period portfolio optimization, and insurance claim prediction, which involve neural networks with (Leaky)-ReLU activation functions. Numerical experiments conducted using real-world datasets illustrate the superior empirical performance of e-TH$\varepsilon$O POULA compared to SGLD, ADAM, and AMSGrad in terms of model accuracy.