Robust Q-Learning for finite ambiguity sets

In this paper we propose a novel $Q$-learning algorithm allowing to solve distributionally robust Markov decision problems for which the ambiguity set of probability measures can be chosen arbitrarily as long as it comprises only a finite amount of measures. Therefore, our approach goes beyond the well-studied cases involving ambiguity sets of balls around some reference measure with the distance to reference measure being measured with respect to the Wasserstein distance or the Kullback--Leibler divergence. Hence, our approach allows the applicant to create ambiguity sets better tailored to her needs and to solve the associated robust Markov decision problem via a $Q$-learning algorithm whose convergence is guaranteed by our main result. Moreover, we showcase in several numerical experiments the tractability of our approach.

Neural networks can detect model-free static arbitrage strategies

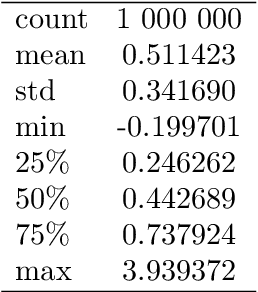
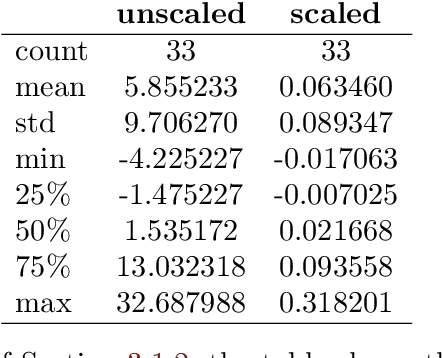
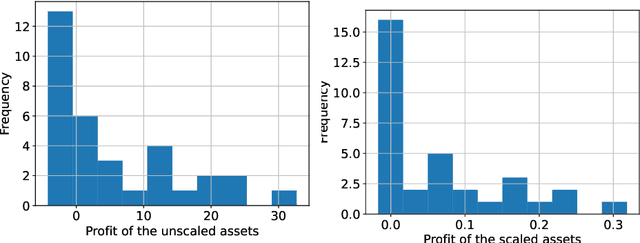
In this paper we demonstrate both theoretically as well as numerically that neural networks can detect model-free static arbitrage opportunities whenever the market admits some. Due to the use of neural networks, our method can be applied to financial markets with a high number of traded securities and ensures almost immediate execution of the corresponding trading strategies. To demonstrate its tractability, effectiveness, and robustness we provide examples using real financial data. From a technical point of view, we prove that a single neural network can approximately solve a class of convex semi-infinite programs, which is the key result in order to derive our theoretical results that neural networks can detect model-free static arbitrage strategies whenever the financial market admits such opportunities.

Robust $Q$-learning Algorithm for Markov Decision Processes under Wasserstein Uncertainty

We present a novel $Q$-learning algorithm to solve distributionally robust Markov decision problems, where the corresponding ambiguity set of transition probabilities for the underlying Markov decision process is a Wasserstein ball around a (possibly estimated) reference measure. We prove convergence of the presented algorithm and provide several examples also using real data to illustrate both the tractability of our algorithm as well as the benefits of considering distributional robustness when solving stochastic optimal control problems, in particular when the estimated distributions turn out to be misspecified in practice.

Markov Decision Processes under Model Uncertainty

We introduce a general framework for Markov decision problems under model uncertainty in a discrete-time infinite horizon setting. By providing a dynamic programming principle we obtain a local-to-global paradigm, namely solving a local, i.e., a one time-step robust optimization problem leads to an optimizer of the global (i.e. infinite time-steps) robust stochastic optimal control problem, as well as to a corresponding worst-case measure. Moreover, we apply this framework to portfolio optimization involving data of the S&P 500. We present two different types of ambiguity sets; one is fully data-driven given by a Wasserstein-ball around the empirical measure, the second one is described by a parametric set of multivariate normal distributions, where the corresponding uncertainty sets of the parameters are estimated from the data. It turns out that in scenarios where the market is volatile or bearish, the optimal portfolio strategies from the corresponding robust optimization problem outperforms the ones without model uncertainty, showcasing the importance of taking model uncertainty into account.

Detecting data-driven robust statistical arbitrage strategies with deep neural networks

We present an approach, based on deep neural networks, that allows identifying robust statistical arbitrage strategies in financial markets. Robust statistical arbitrage strategies refer to self-financing trading strategies that enable profitable trading under model ambiguity. The presented novel methodology does not suffer from the curse of dimensionality nor does it depend on the identification of cointegrated pairs of assets and is therefore applicable even on high-dimensional financial markets or in markets where classical pairs trading approaches fail. Moreover, we provide a method to build an ambiguity set of admissible probability measures that can be derived from observed market data. Thus, the approach can be considered as being model-free and entirely data-driven. We showcase the applicability of our method by providing empirical investigations with highly profitable trading performances even in 50 dimensions, during financial crises, and when the cointegration relationship between asset pairs stops to persist.

A deep learning approach to data-driven model-free pricing and to martingale optimal transport

We introduce a novel and highly tractable supervised learning approach based on neural networks that can be applied for the computation of model-free price bounds of, potentially high-dimensional, financial derivatives and for the determination of optimal hedging strategies attaining these bounds. In particular, our methodology allows to train a single neural network offline and then to use it online for the fast determination of model-free price bounds of a whole class of financial derivatives with current market data. We show the applicability of this approach and highlight its accuracy in several examples involving real market data. Further, we show how a neural network can be trained to solve martingale optimal transport problems involving fixed marginal distributions instead of financial market data.