Daiying Yin
A Structure-Preserving Kernel Method for Learning Hamiltonian Systems
Mar 15, 2024Abstract:A structure-preserving kernel ridge regression method is presented that allows the recovery of potentially high-dimensional and nonlinear Hamiltonian functions out of datasets made of noisy observations of Hamiltonian vector fields. The method proposes a closed-form solution that yields excellent numerical performances that surpass other techniques proposed in the literature in this setup. From the methodological point of view, the paper extends kernel regression methods to problems in which loss functions involving linear functions of gradients are required and, in particular, a differential reproducing property and a Representer Theorem are proved in this context. The relation between the structure-preserving kernel estimator and the Gaussian posterior mean estimator is analyzed. A full error analysis is conducted that provides convergence rates using fixed and adaptive regularization parameters. The good performance of the proposed estimator is illustrated with various numerical experiments.
Detecting data-driven robust statistical arbitrage strategies with deep neural networks
Mar 10, 2022



Abstract:We present an approach, based on deep neural networks, that allows identifying robust statistical arbitrage strategies in financial markets. Robust statistical arbitrage strategies refer to self-financing trading strategies that enable profitable trading under model ambiguity. The presented novel methodology does not suffer from the curse of dimensionality nor does it depend on the identification of cointegrated pairs of assets and is therefore applicable even on high-dimensional financial markets or in markets where classical pairs trading approaches fail. Moreover, we provide a method to build an ambiguity set of admissible probability measures that can be derived from observed market data. Thus, the approach can be considered as being model-free and entirely data-driven. We showcase the applicability of our method by providing empirical investigations with highly profitable trading performances even in 50 dimensions, during financial crises, and when the cointegration relationship between asset pairs stops to persist.
Performance Optimization for Federated Person Re-identification via Benchmark Analysis
Aug 26, 2020
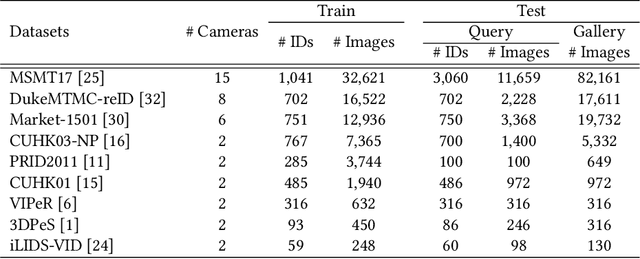
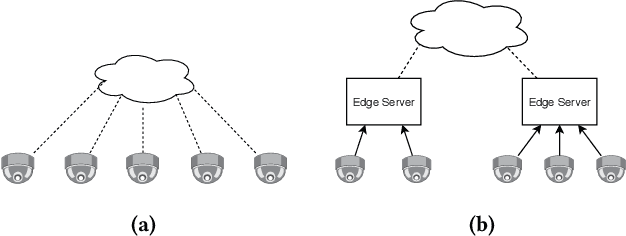
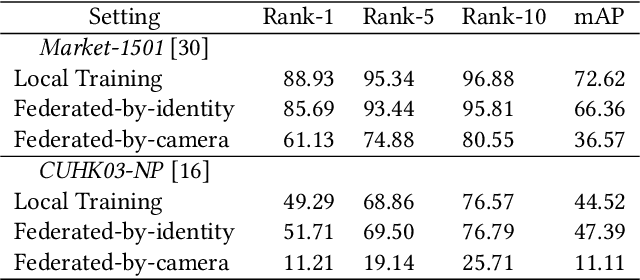
Abstract:Federated learning is a privacy-preserving machine learning technique that learns a shared model across decentralized clients. It can alleviate privacy concerns of personal re-identification, an important computer vision task. In this work, we implement federated learning to person re-identification (FedReID) and optimize its performance affected by statistical heterogeneity in the real-world scenario. We first construct a new benchmark to investigate the performance of FedReID. This benchmark consists of (1) nine datasets with different volumes sourced from different domains to simulate the heterogeneous situation in reality, (2) two federated scenarios, and (3) an enhanced federated algorithm for FedReID. The benchmark analysis shows that the client-edge-cloud architecture, represented by the federated-by-dataset scenario, has better performance than client-server architecture in FedReID. It also reveals the bottlenecks of FedReID under the real-world scenario, including poor performance of large datasets caused by unbalanced weights in model aggregation and challenges in convergence. Then we propose two optimization methods: (1) To address the unbalanced weight problem, we propose a new method to dynamically change the weights according to the scale of model changes in clients in each training round; (2) To facilitate convergence, we adopt knowledge distillation to refine the server model with knowledge generated from client models on a public dataset. Experiment results demonstrate that our strategies can achieve much better convergence with superior performance on all datasets. We believe that our work will inspire the community to further explore the implementation of federated learning on more computer vision tasks in real-world scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge