Enhancing Gradient-based Discrete Sampling via Parallel Tempering

While gradient-based discrete samplers are effective in sampling from complex distributions, they are susceptible to getting trapped in local minima, particularly in high-dimensional, multimodal discrete distributions, owing to the discontinuities inherent in these landscapes. To circumvent this issue, we combine parallel tempering, also known as replica exchange, with the discrete Langevin proposal and develop the Parallel Tempering enhanced Discrete Langevin Proposal (PTDLP), which are simulated at a series of temperatures. Significant energy differences prompt sample swaps, which are governed by a Metropolis criterion specifically designed for discrete sampling to ensure detailed balance is maintained. Additionally, we introduce an automatic scheme to determine the optimal temperature schedule and the number of chains, ensuring adaptability across diverse tasks with minimal tuning. Theoretically, we establish that our algorithm converges non-asymptotically to the target energy and exhibits faster mixing compared to a single chain. Empirical results further emphasize the superiority of our method in sampling from complex, multimodal discrete distributions, including synthetic problems, restricted Boltzmann machines, and deep energy-based models.

Non-asymptotic convergence analysis of the stochastic gradient Hamiltonian Monte Carlo algorithm with discontinuous stochastic gradient with applications to training of ReLU neural networks

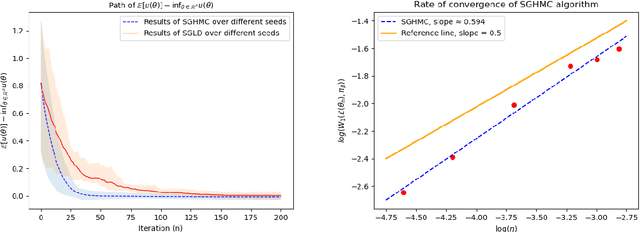
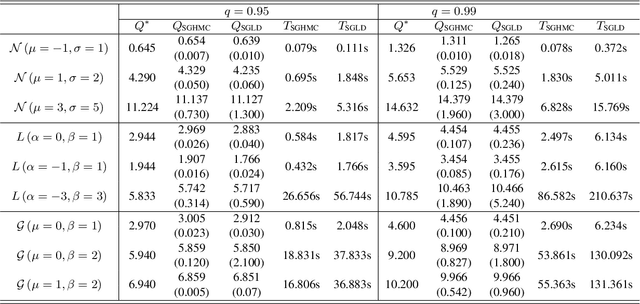
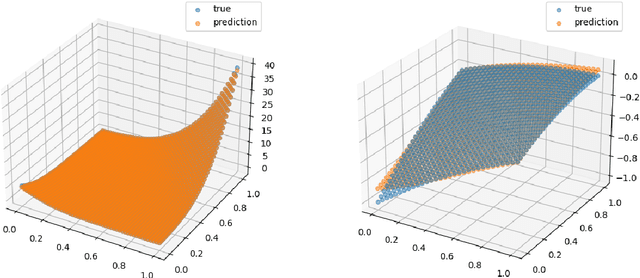
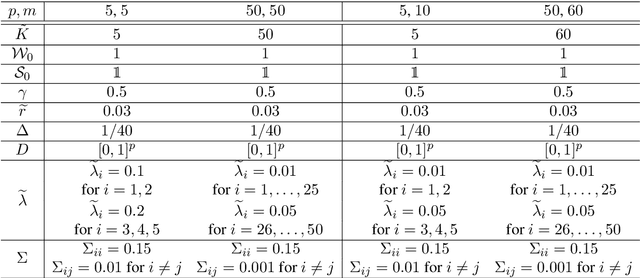
In this paper, we provide a non-asymptotic analysis of the convergence of the stochastic gradient Hamiltonian Monte Carlo (SGHMC) algorithm to a target measure in Wasserstein-1 and Wasserstein-2 distance. Crucially, compared to the existing literature on SGHMC, we allow its stochastic gradient to be discontinuous. This allows us to provide explicit upper bounds, which can be controlled to be arbitrarily small, for the expected excess risk of non-convex stochastic optimization problems with discontinuous stochastic gradients, including, among others, the training of neural networks with ReLU activation function. To illustrate the applicability of our main results, we consider numerical experiments on quantile estimation and on several optimization problems involving ReLU neural networks relevant in finance and artificial intelligence.