Non-asymptotic estimates for accelerated high order Langevin Monte Carlo algorithms
Paper and Code
May 09, 2024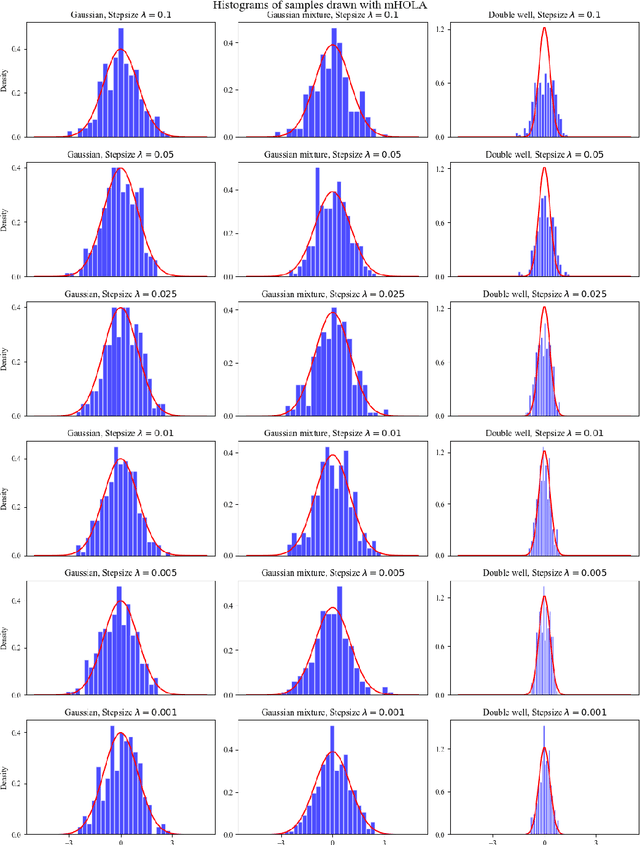
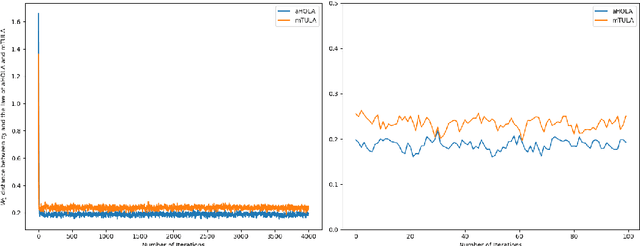
In this paper, we propose two new algorithms, namely aHOLA and aHOLLA, to sample from high-dimensional target distributions with possibly super-linearly growing potentials. We establish non-asymptotic convergence bounds for aHOLA in Wasserstein-1 and Wasserstein-2 distances with rates of convergence equal to $1+q/2$ and $1/2+q/4$, respectively, under a local H\"{o}lder condition with exponent $q\in(0,1]$ and a convexity at infinity condition on the potential of the target distribution. Similar results are obtained for aHOLLA under certain global continuity conditions and a dissipativity condition. Crucially, we achieve state-of-the-art rates of convergence of the proposed algorithms in the non-convex setting which are higher than those of the existing algorithms. Numerical experiments are conducted to sample from several distributions and the results support our main findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge