Dong-Young Lim
Controllable Machine Unlearning via Gradient Pivoting
Oct 22, 2025Abstract:Machine unlearning (MU) aims to remove the influence of specific data from a trained model. However, approximate unlearning methods, often formulated as a single-objective optimization (SOO) problem, face a critical trade-off between unlearning efficacy and model fidelity. This leads to three primary challenges: the risk of over-forgetting, a lack of fine-grained control over the unlearning process, and the absence of metrics to holistically evaluate the trade-off. To address these issues, we reframe MU as a multi-objective optimization (MOO) problem. We then introduce a novel algorithm, Controllable Unlearning by Pivoting Gradient (CUP), which features a unique pivoting mechanism. Unlike traditional MOO methods that converge to a single solution, CUP's mechanism is designed to controllably navigate the entire Pareto frontier. This navigation is governed by a single intuitive hyperparameter, the `unlearning intensity', which allows for precise selection of a desired trade-off. To evaluate this capability, we adopt the hypervolume indicator, a metric that captures both the quality and diversity of the entire set of solutions an algorithm can generate. Our experimental results demonstrate that CUP produces a superior set of Pareto-optimal solutions, consistently outperforming existing methods across various vision tasks.
Flatness-Aware Stochastic Gradient Langevin Dynamics
Oct 02, 2025Abstract:Generalization in deep learning is closely tied to the pursuit of flat minima in the loss landscape, yet classical Stochastic Gradient Langevin Dynamics (SGLD) offers no mechanism to bias its dynamics toward such low-curvature solutions. This work introduces Flatness-Aware Stochastic Gradient Langevin Dynamics (fSGLD), designed to efficiently and provably seek flat minima in high-dimensional nonconvex optimization problems. At each iteration, fSGLD uses the stochastic gradient evaluated at parameters perturbed by isotropic Gaussian noise, commonly referred to as Random Weight Perturbation (RWP), thereby optimizing a randomized-smoothing objective that implicitly captures curvature information. Leveraging these properties, we prove that the invariant measure of fSGLD stays close to a stationary measure concentrated on the global minimizers of a loss function regularized by the Hessian trace whenever the inverse temperature and the scale of random weight perturbation are properly coupled. This result provides a rigorous theoretical explanation for the benefits of random weight perturbation. In particular, we establish non-asymptotic convergence guarantees in Wasserstein distance with the best known rate and derive an excess-risk bound for the Hessian-trace regularized objective. Extensive experiments on noisy-label and large-scale vision tasks, in both training-from-scratch and fine-tuning settings, demonstrate that fSGLD achieves superior or comparable generalization and robustness to baseline algorithms while maintaining the computational cost of SGD, about half that of SAM. Hessian-spectrum analysis further confirms that fSGLD converges to significantly flatter minima.
Modeling Irregular Astronomical Time Series with Neural Stochastic Delay Differential Equations
Aug 24, 2025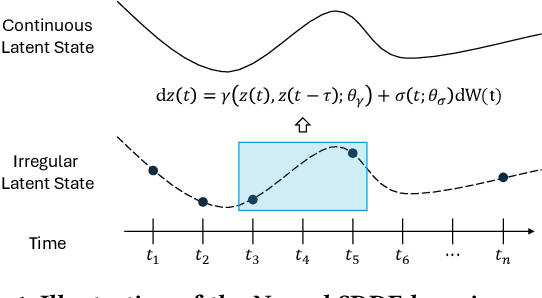
Abstract:Astronomical time series from large-scale surveys like LSST are often irregularly sampled and incomplete, posing challenges for classification and anomaly detection. We introduce a new framework based on Neural Stochastic Delay Differential Equations (Neural SDDEs) that combines stochastic modeling with neural networks to capture delayed temporal dynamics and handle irregular observations. Our approach integrates a delay-aware neural architecture, a numerical solver for SDDEs, and mechanisms to robustly learn from noisy, sparse sequences. Experiments on irregularly sampled astronomical data demonstrate strong classification accuracy and effective detection of novel astrophysical events, even with partial labels. This work highlights Neural SDDEs as a principled and practical tool for time series analysis under observational constraints.
TANDEM: Temporal Attention-guided Neural Differential Equations for Missingness in Time Series Classification
Aug 24, 2025Abstract:Handling missing data in time series classification remains a significant challenge in various domains. Traditional methods often rely on imputation, which may introduce bias or fail to capture the underlying temporal dynamics. In this paper, we propose TANDEM (Temporal Attention-guided Neural Differential Equations for Missingness), an attention-guided neural differential equation framework that effectively classifies time series data with missing values. Our approach integrates raw observation, interpolated control path, and continuous latent dynamics through a novel attention mechanism, allowing the model to focus on the most informative aspects of the data. We evaluate TANDEM on 30 benchmark datasets and a real-world medical dataset, demonstrating its superiority over existing state-of-the-art methods. Our framework not only improves classification accuracy but also provides insights into the handling of missing data, making it a valuable tool in practice.
DGSAM: Domain Generalization via Individual Sharpness-Aware Minimization
Mar 30, 2025Abstract:Domain generalization (DG) aims to learn models that can generalize well to unseen domains by training only on a set of source domains. Sharpness-Aware Minimization (SAM) has been a popular approach for this, aiming to find flat minima in the total loss landscape. However, we show that minimizing the total loss sharpness does not guarantee sharpness across individual domains. In particular, SAM can converge to fake flat minima, where the total loss may exhibit flat minima, but sharp minima are present in individual domains. Moreover, the current perturbation update in gradient ascent steps is ineffective in directly updating the sharpness of individual domains. Motivated by these findings, we introduce a novel DG algorithm, Decreased-overhead Gradual Sharpness-Aware Minimization (DGSAM), that applies gradual domain-wise perturbation to reduce sharpness consistently across domains while maintaining computational efficiency. Our experiments demonstrate that DGSAM outperforms state-of-the-art DG methods, achieving improved robustness to domain shifts and better performance across various benchmarks, while reducing computational overhead compared to SAM.
Dual Cone Gradient Descent for Training Physics-Informed Neural Networks
Sep 27, 2024Abstract:Physics-informed neural networks (PINNs) have emerged as a prominent approach for solving partial differential equations (PDEs) by minimizing a combined loss function that incorporates both boundary loss and PDE residual loss. Despite their remarkable empirical performance in various scientific computing tasks, PINNs often fail to generate reasonable solutions, and such pathological behaviors remain difficult to explain and resolve. In this paper, we identify that PINNs can be adversely trained when gradients of each loss function exhibit a significant imbalance in their magnitudes and present a negative inner product value. To address these issues, we propose a novel optimization framework, Dual Cone Gradient Descent (DCGD), which adjusts the direction of the updated gradient to ensure it falls within a dual cone region. This region is defined as a set of vectors where the inner products with both the gradients of the PDE residual loss and the boundary loss are non-negative. Theoretically, we analyze the convergence properties of DCGD algorithms in a non-convex setting. On a variety of benchmark equations, we demonstrate that DCGD outperforms other optimization algorithms in terms of various evaluation metrics. In particular, DCGD achieves superior predictive accuracy and enhances the stability of training for failure modes of PINNs and complex PDEs, compared to existing optimally tuned models. Moreover, DCGD can be further improved by combining it with popular strategies for PINNs, including learning rate annealing and the Neural Tangent Kernel (NTK).
On diffusion-based generative models and their error bounds: The log-concave case with full convergence estimates
Nov 22, 2023

Abstract:We provide full theoretical guarantees for the convergence behaviour of diffusion-based generative models under the assumption of strongly logconcave data distributions while our approximating class of functions used for score estimation is made of Lipschitz continuous functions. We demonstrate via a motivating example, sampling from a Gaussian distribution with unknown mean, the powerfulness of our approach. In this case, explicit estimates are provided for the associated optimization problem, i.e. score approximation, while these are combined with the corresponding sampling estimates. As a result, we obtain the best known upper bound estimates in terms of key quantities of interest, such as the dimension and rates of convergence, for the Wasserstein-2 distance between the data distribution (Gaussian with unknown mean) and our sampling algorithm. Beyond the motivating example and in order to allow for the use of a diverse range of stochastic optimizers, we present our results using an $L^2$-accurate score estimation assumption, which crucially is formed under an expectation with respect to the stochastic optimizer and our novel auxiliary process that uses only known information. This approach yields the best known convergence rate for our sampling algorithm.
Langevin dynamics based algorithm e-TH$\varepsilon$O POULA for stochastic optimization problems with discontinuous stochastic gradient
Oct 24, 2022
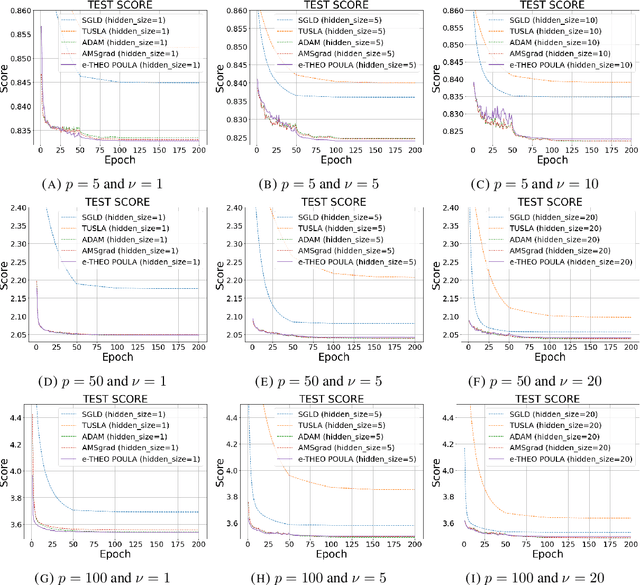
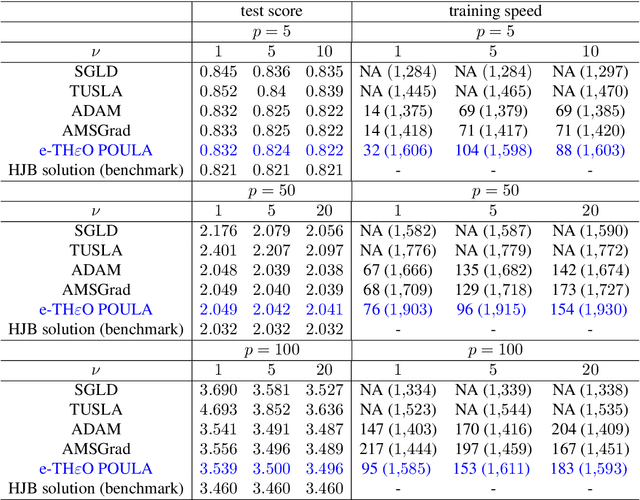
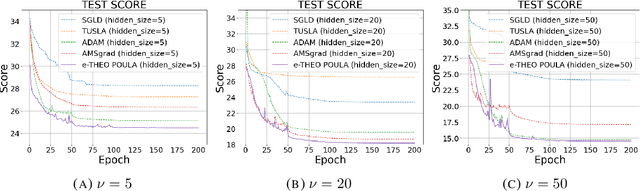
Abstract:We introduce a new Langevin dynamics based algorithm, called e-TH$\varepsilon$O POULA, to solve optimization problems with discontinuous stochastic gradients which naturally appear in real-world applications such as quantile estimation, vector quantization, CVaR minimization, and regularized optimization problems involving ReLU neural networks. We demonstrate both theoretically and numerically the applicability of the e-TH$\varepsilon$O POULA algorithm. More precisely, under the conditions that the stochastic gradient is locally Lipschitz in average and satisfies a certain convexity at infinity condition, we establish non-asymptotic error bounds for e-TH$\varepsilon$O POULA in Wasserstein distances and provide a non-asymptotic estimate for the expected excess risk, which can be controlled to be arbitrarily small. Three key applications in finance and insurance are provided, namely, multi-period portfolio optimization, transfer learning in multi-period portfolio optimization, and insurance claim prediction, which involve neural networks with (Leaky)-ReLU activation functions. Numerical experiments conducted using real-world datasets illustrate the superior empirical performance of e-TH$\varepsilon$O POULA compared to SGLD, ADAM, and AMSGrad in terms of model accuracy.
Non-asymptotic estimates for TUSLA algorithm for non-convex learning with applications to neural networks with ReLU activation function
Jul 19, 2021

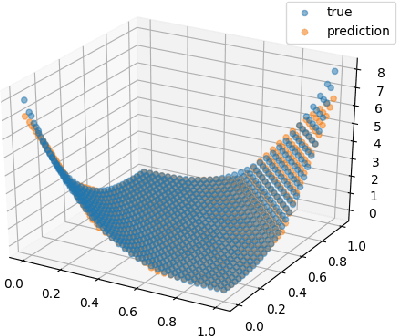

Abstract:We consider non-convex stochastic optimization problems where the objective functions have super-linearly growing and discontinuous stochastic gradients. In such a setting, we provide a non-asymptotic analysis for the tamed unadjusted stochastic Langevin algorithm (TUSLA) introduced in Lovas et al. (2021). In particular, we establish non-asymptotic error bounds for the TUSLA algorithm in Wasserstein-1 and Wasserstein-2 distances. The latter result enables us to further derive non-asymptotic estimates for the expected excess risk. To illustrate the applicability of the main results, we consider an example from transfer learning with ReLU neural networks, which represents a key paradigm in machine learning. Numerical experiments are presented for the aforementioned example which supports our theoretical findings. Hence, in this setting, we demonstrate both theoretically and numerically that the TUSLA algorithm can solve the optimization problem involving neural networks with ReLU activation function. Besides, we provide simulation results for synthetic examples where popular algorithms, e.g. ADAM, AMSGrad, RMSProp, and (vanilla) SGD, may fail to find the minimizer of the objective functions due to the super-linear growth and the discontinuity of the corresponding stochastic gradient, while the TUSLA algorithm converges rapidly to the optimal solution.
Polygonal Unadjusted Langevin Algorithms: Creating stable and efficient adaptive algorithms for neural networks
May 28, 2021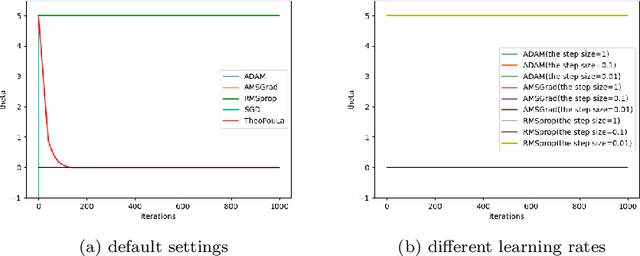

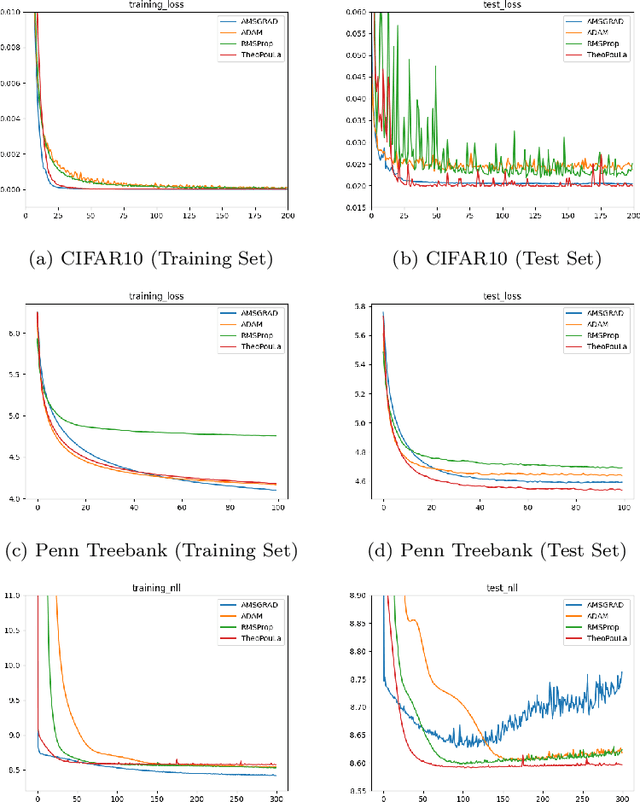

Abstract:We present a new class of adaptive stochastic optimization algorithms, which overcomes many of the known shortcomings of popular adaptive optimizers that are currently used for the fine tuning of artificial neural networks (ANNs). Its underpinning theory relies on advances of Euler's polygonal approximations for stochastic differential equations (SDEs) with monotone coefficients. As a result, it inherits the stability properties of tamed algorithms, while it addresses other known issues, e.g. vanishing gradients in ANNs. In particular, we provide an nonasymptotic analysis and full theoretical guarantees for the convergence properties of an algorithm of this novel class, which we named TH$\varepsilon$O POULA (or, simply, TheoPouLa). Finally, several experiments are presented with different types of ANNs, which show the superior performance of TheoPouLa over many popular adaptive optimization algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge