Convergence proof for stochastic gradient descent in the training of deep neural networks with ReLU activation for constant target functions

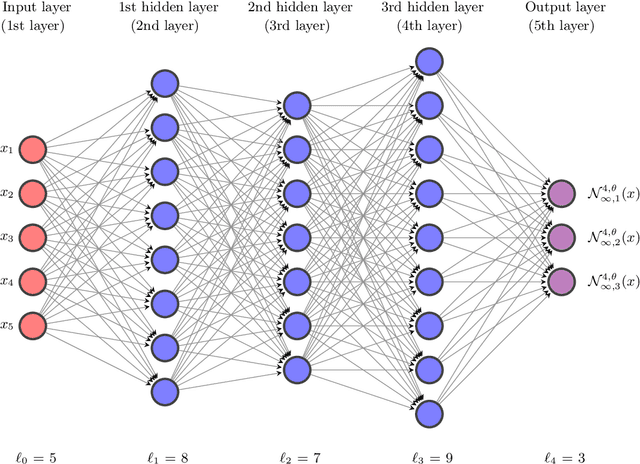
In many numerical simulations stochastic gradient descent (SGD) type optimization methods perform very effectively in the training of deep neural networks (DNNs) but till this day it remains an open problem of research to provide a mathematical convergence analysis which rigorously explains the success of SGD type optimization methods in the training of DNNs. In this work we study SGD type optimization methods in the training of fully-connected feedforward DNNs with rectified linear unit (ReLU) activation. We first establish general regularity properties for the risk functions and their generalized gradient functions appearing in the training of such DNNs and, thereafter, we investigate the plain vanilla SGD optimization method in the training of such DNNs under the assumption that the target function under consideration is a constant function. Specifically, we prove under the assumption that the learning rates (the step sizes of the SGD optimization method) are sufficiently small but not $L^1$-summable and under the assumption that the target function is a constant function that the expectation of the riskof the considered SGD process converges in the training of such DNNs to zero as the number of SGD steps increases to infinity.

An overview on deep learning-based approximation methods for partial differential equations

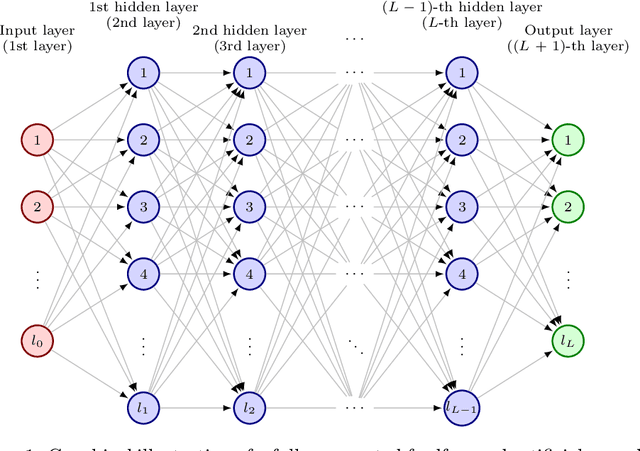
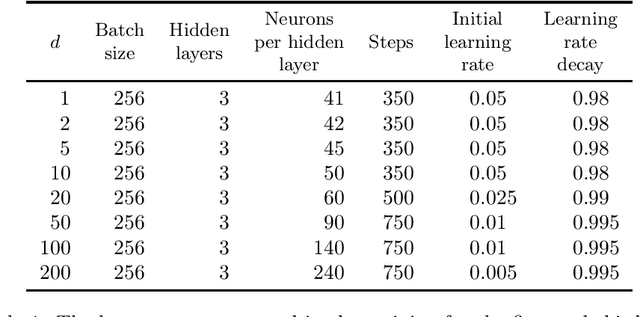
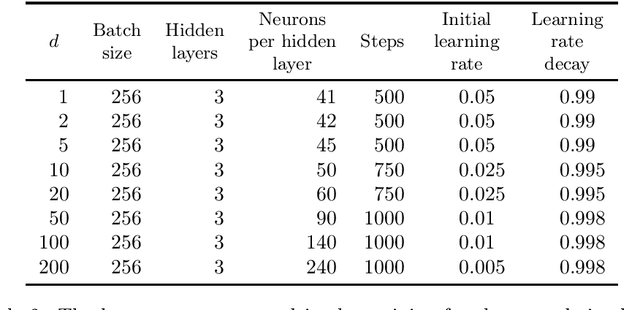
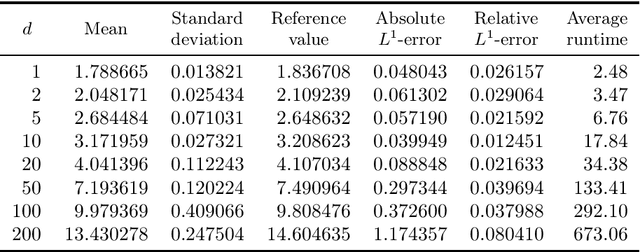
It is one of the most challenging problems in applied mathematics to approximatively solve high-dimensional partial differential equations (PDEs). Recently, several deep learning-based approximation algorithms for attacking this problem have been proposed and tested numerically on a number of examples of high-dimensional PDEs. This has given rise to a lively field of research in which deep learning-based methods and related Monte Carlo methods are applied to the approximation of high-dimensional PDEs. In this article we offer an introduction to this field of research, we review some of the main ideas of deep learning-based approximation methods for PDEs, we revisit one of the central mathematical results for deep neural network approximations for PDEs, and we provide an overview of the recent literature in this area of research.