Solving Rubik's Cube Without Tricky Sampling

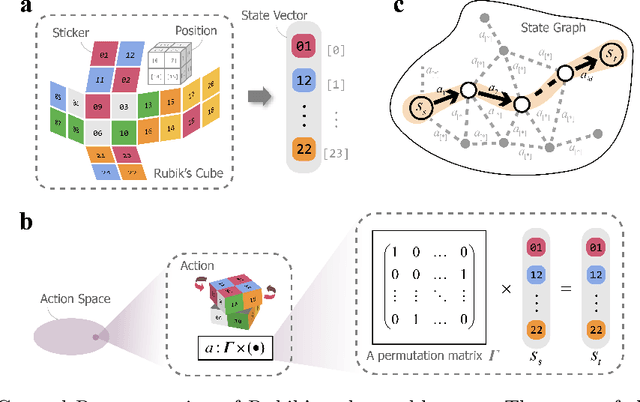
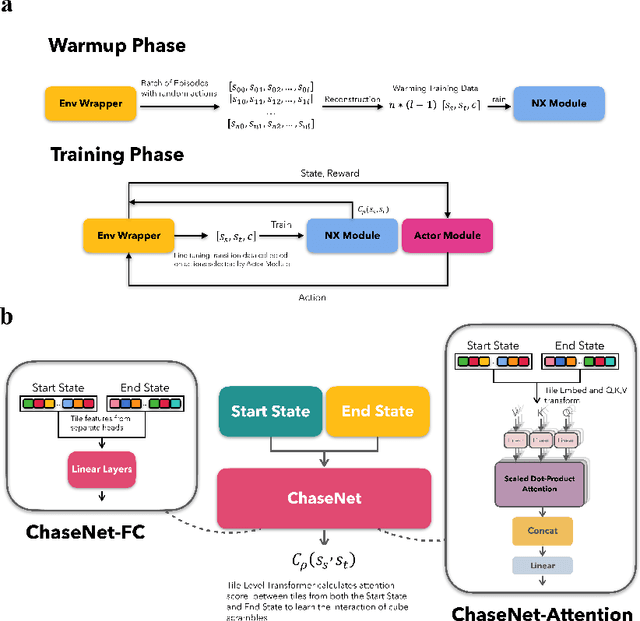
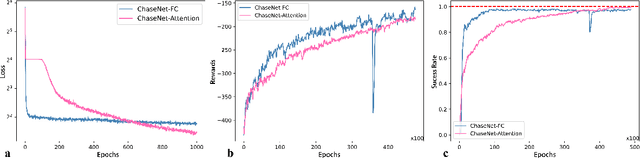
The Rubiks Cube, with its vast state space and sparse reward structure, presents a significant challenge for reinforcement learning (RL) due to the difficulty of reaching rewarded states. Previous research addressed this by propagating cost-to-go estimates from the solved state and incorporating search techniques. These approaches differ from human strategies that start from fully scrambled cubes, which can be tricky for solving a general sparse-reward problem. In this paper, we introduce a novel RL algorithm using policy gradient methods to solve the Rubiks Cube without relying on near solved-state sampling. Our approach employs a neural network to predict cost patterns between states, allowing the agent to learn directly from scrambled states. Our method was tested on the 2x2x2 Rubiks Cube, where the cube was scrambled 50,000 times, and the model successfully solved it in over 99.4% of cases. Notably, this result was achieved using only the policy network without relying on tree search as in previous methods, demonstrating its effectiveness and potential for broader applications in sparse-reward problems.

GWQ: Gradient-Aware Weight Quantization for Large Language Models

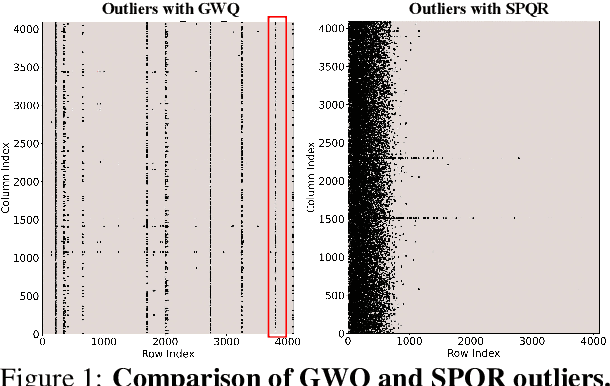
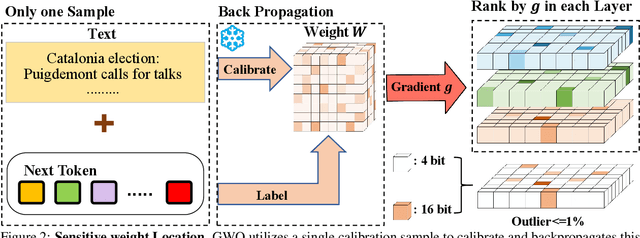
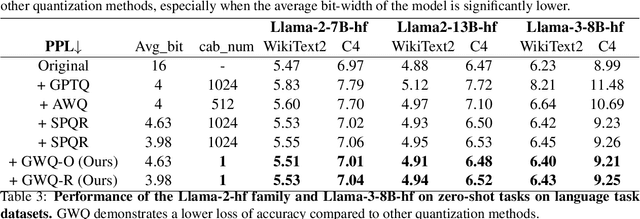
Large language models (LLMs) show impressive performance in solving complex languagetasks. However, its large number of parameterspresent significant challenges for the deployment and application of the model on edge devices. Compressing large language models to low bits can enable them to run on resource-constrained devices, often leading to performance degradation. To address this problem, we propose gradient-aware weight quantization (GWQ), the first quantization approach for low-bit weight quantization that leverages gradients to localize outliers, requiring only a minimal amount of calibration data for outlier detection. GWQ retains the weights corresponding to the top 1% outliers preferentially at FP16 precision, while the remaining non-outlier weights are stored in a low-bit format. GWQ found experimentally that utilizing the sensitive weights in the gradient localization model is more scientific compared to utilizing the sensitive weights in the Hessian matrix localization model. Compared to current quantization methods, GWQ can be applied to multiple language models and achieves lower PPL on the WikiText2 and C4 dataset. In the zero-shot task, GWQ quantized models have higher accuracy compared to other quantization methods.GWQ is also suitable for multimodal model quantization, and the quantized Qwen-VL family model is more accurate than other methods. zero-shot target detection task dataset RefCOCO outperforms the current stat-of-the-arts method SPQR. GWQ achieves 1.2x inference speedup in comparison to the original model, and effectively reduces the inference memory.

An Overview on Machine Learning Methods for Partial Differential Equations: from Physics Informed Neural Networks to Deep Operator Learning

The approximation of solutions of partial differential equations (PDEs) with numerical algorithms is a central topic in applied mathematics. For many decades, various types of methods for this purpose have been developed and extensively studied. One class of methods which has received a lot of attention in recent years are machine learning-based methods, which typically involve the training of artificial neural networks (ANNs) by means of stochastic gradient descent type optimization methods. While approximation methods for PDEs using ANNs have first been proposed in the 1990s they have only gained wide popularity in the last decade with the rise of deep learning. This article aims to provide an introduction to some of these methods and the mathematical theory on which they are based. We discuss methods such as physics-informed neural networks (PINNs) and deep BSDE methods and consider several operator learning approaches.