Learning the conditional law: signatures and conditional GANs in filtering and prediction of diffusion processes

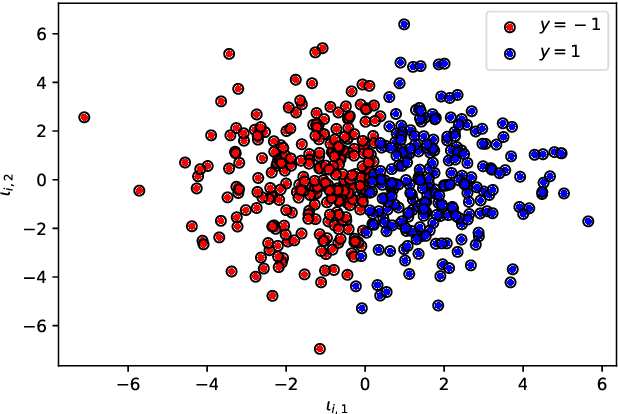
We consider the filtering and prediction problem for a diffusion process. The signal and observation are modeled by stochastic differential equations (SDEs) driven by Wiener processes. In classical estimation theory, measure-valued stochastic partial differential equations (SPDEs) are derived for the filtering and prediction measures. These equations can be hard to solve numerically. We provide an approximation algorithm using conditional generative adversarial networks (GANs) and signatures, an object from rough path theory. The signature of a sufficiently smooth path determines the path completely. In some cases, GANs based on signatures have been shown to efficiently approximate the law of a stochastic process. In this paper we extend this method to approximate the prediction measure conditional to noisy observation. We use controlled differential equations (CDEs) as universal approximators to propose an estimator for the conditional and prediction law. We show well-posedness in providing a rigorous mathematical framework. Numerical results show the efficiency of our algorithm.

Sig-Wasserstein GANs for Time Series Generation

Synthetic data is an emerging technology that can significantly accelerate the development and deployment of AI machine learning pipelines. In this work, we develop high-fidelity time-series generators, the SigWGAN, by combining continuous-time stochastic models with the newly proposed signature $W_1$ metric. The former are the Logsig-RNN models based on the stochastic differential equations, whereas the latter originates from the universal and principled mathematical features to characterize the measure induced by time series. SigWGAN allows turning computationally challenging GAN min-max problem into supervised learning while generating high fidelity samples. We validate the proposed model on both synthetic data generated by popular quantitative risk models and empirical financial data. Codes are available at https://github.com/SigCGANs/Sig-Wasserstein-GANs.git.

Robust pricing and hedging via neural SDEs

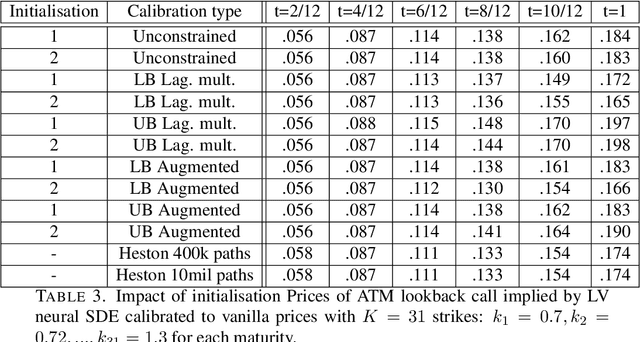
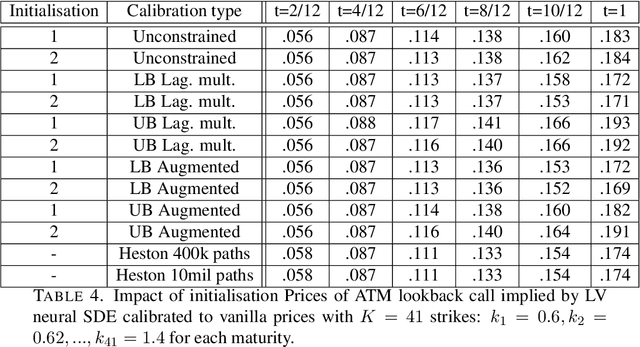
Mathematical modelling is ubiquitous in the financial industry and drives key decision processes. Any given model provides only a crude approximation to reality and the risk of using an inadequate model is hard to detect and quantify. By contrast, modern data science techniques are opening the door to more robust and data-driven model selection mechanisms. However, most machine learning models are "black-boxes" as individual parameters do not have meaningful interpretation. The aim of this paper is to combine the above approaches achieving the best of both worlds. Combining neural networks with risk models based on classical stochastic differential equations (SDEs), we find robust bounds for prices of derivatives and the corresponding hedging strategies while incorporating relevant market data. The resulting model called neural SDE is an instantiation of generative models and is closely linked with the theory of causal optimal transport. Neural SDEs allow consistent calibration under both the risk-neutral and the real-world measures. Thus the model can be used to simulate market scenarios needed for assessing risk profiles and hedging strategies. We develop and analyse novel algorithms needed for efficient use of neural SDEs. We validate our approach with numerical experiments using both local and stochastic volatility models.

Multi-index Antithetic Stochastic Gradient Algorithm

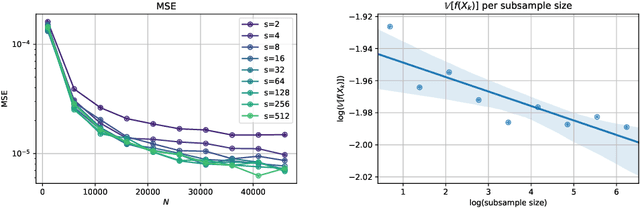
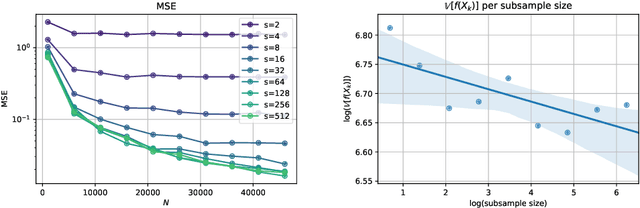
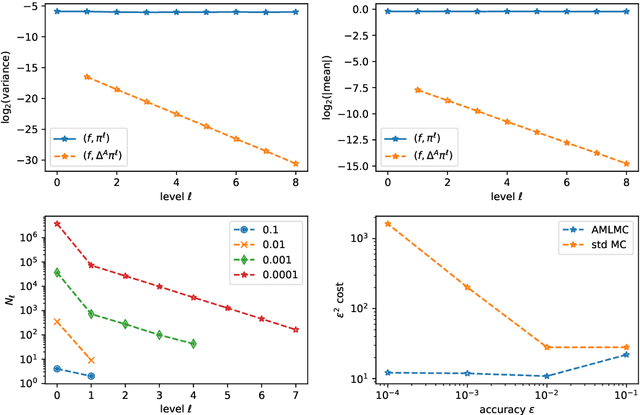
Stochastic Gradient Algorithms (SGAs) are ubiquitous in computational statistics, machine learning and optimisation. Recent years have brought an influx of interest in SGAs and the non-asymptotic analysis of their bias is by now well-developed. However, in order to fully understand the efficiency of Monte Carlo algorithms utilizing stochastic gradients, one also needs to carry out the analysis of their variance, which turns out to be problem-specific. For this reason, there is no systematic theory that would specify the optimal choice of the random approximation of the gradient in SGAs for a given data regime. Furthermore, while there have been numerous attempts to reduce the variance of SGAs, these typically exploit a particular structure of the sampled distribution. In this paper we use the Multi-index Monte Carlo apparatus combined with the antithetic approach to construct the Multi-index Antithetic Stochastic Gradient Algorithm (MASGA), which can be used to sample from any probability distribution. This, to our knowledge, is the first SGA that, for all data regimes and without relying on any specific structure of the target measure, achieves performance on par with Monte Carlo estimators that have access to unbiased samples from the distribution of interest. In other words, MASGA is an optimal estimator from the error-computational cost perspective within the class of Monte Carlo estimators.