Multi-index Antithetic Stochastic Gradient Algorithm
Paper and Code
Jun 10, 2020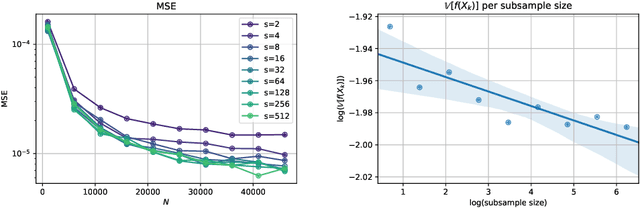
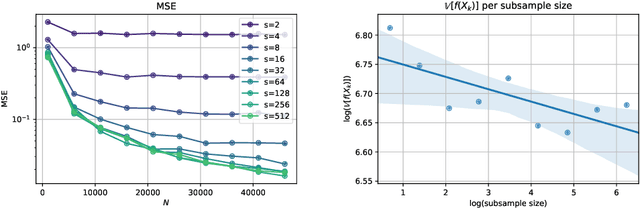
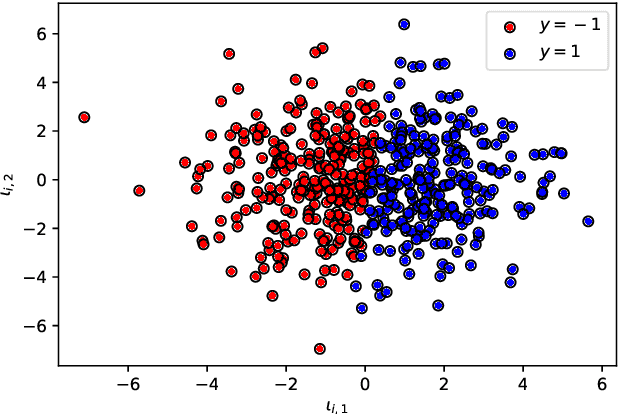
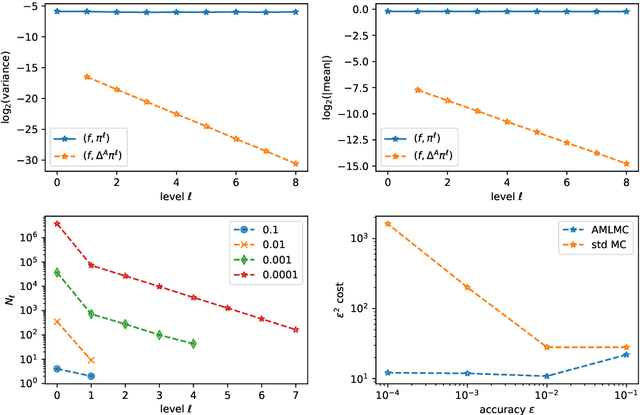
Stochastic Gradient Algorithms (SGAs) are ubiquitous in computational statistics, machine learning and optimisation. Recent years have brought an influx of interest in SGAs and the non-asymptotic analysis of their bias is by now well-developed. However, in order to fully understand the efficiency of Monte Carlo algorithms utilizing stochastic gradients, one also needs to carry out the analysis of their variance, which turns out to be problem-specific. For this reason, there is no systematic theory that would specify the optimal choice of the random approximation of the gradient in SGAs for a given data regime. Furthermore, while there have been numerous attempts to reduce the variance of SGAs, these typically exploit a particular structure of the sampled distribution. In this paper we use the Multi-index Monte Carlo apparatus combined with the antithetic approach to construct the Multi-index Antithetic Stochastic Gradient Algorithm (MASGA), which can be used to sample from any probability distribution. This, to our knowledge, is the first SGA that, for all data regimes and without relying on any specific structure of the target measure, achieves performance on par with Monte Carlo estimators that have access to unbiased samples from the distribution of interest. In other words, MASGA is an optimal estimator from the error-computational cost perspective within the class of Monte Carlo estimators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge