Central Limit Theorem for ergodic averages of Markov chains \& the comparison of sampling algorithms for heavy-tailed distributions

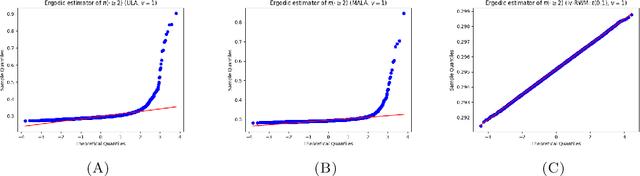
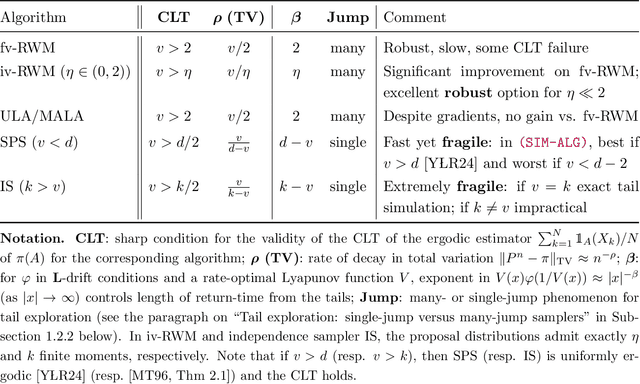
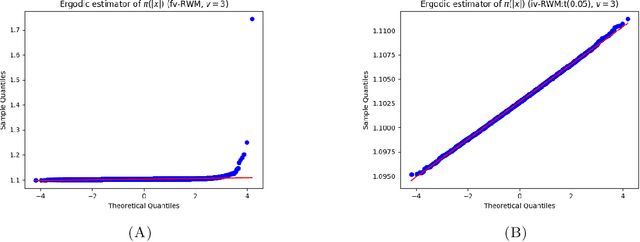
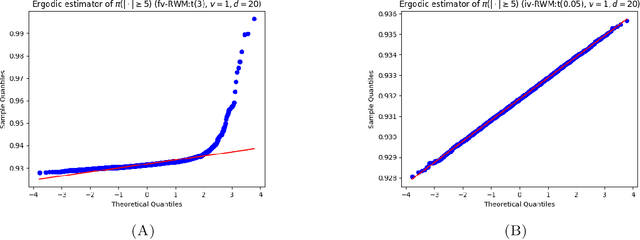
Establishing central limit theorems (CLTs) for ergodic averages of Markov chains is a fundamental problem in probability and its applications. Since the seminal work~\cite{MR834478}, a vast literature has emerged on the sufficient conditions for such CLTs. To counterbalance this, the present paper provides verifiable necessary conditions for CLTs of ergodic averages of Markov chains on general state spaces. Our theory is based on drift conditions, which also yield lower bounds on the rates of convergence to stationarity in various metrics. The validity of the ergodic CLT is of particular importance for sampling algorithms, where it underpins the error analysis of estimators in Bayesian statistics and machine learning. Although heavy-tailed sampling is of central importance in applications, the characterisation of the CLT and the convergence rates are theoretically poorly understood for almost all practically-used Markov chain Monte Carlo (MCMC) algorithms. In this setting our results provide sharp conditions on the validity of the ergodic CLT and establish convergence rates for large families of MCMC sampling algorithms for heavy-tailed targets. Our study includes a rather complete analyses for random walk Metropolis samplers (with finite- and infinite-variance proposals), Metropolis-adjusted and unadjusted Langevin algorithms and the stereographic projection sampler (as well as the independence sampler). By providing these sharp results via our practical drift conditions, our theory offers significant insights into the problems of algorithm selection and comparison for sampling heavy-tailed distributions (see short YouTube presentations~\cite{YouTube_talk} describing our \href{https://youtu.be/m2y7U4cEqy4}{\underline{theory}} and \href{https://youtu.be/w8I_oOweuko}{\underline{applications}}).

Non-asymptotic bounds for forward processes in denoising diffusions: Ornstein-Uhlenbeck is hard to beat

Denoising diffusion probabilistic models (DDPMs) represent a recent advance in generative modelling that has delivered state-of-the-art results across many domains of applications. Despite their success, a rigorous theoretical understanding of the error within DDPMs, particularly the non-asymptotic bounds required for the comparison of their efficiency, remain scarce. Making minimal assumptions on the initial data distribution, allowing for example the manifold hypothesis, this paper presents explicit non-asymptotic bounds on the forward diffusion error in total variation (TV), expressed as a function of the terminal time $T$. We parametrise multi-modal data distributions in terms of the distance $R$ to their furthest modes and consider forward diffusions with additive and multiplicative noise. Our analysis rigorously proves that, under mild assumptions, the canonical choice of the Ornstein-Uhlenbeck (OU) process cannot be significantly improved in terms of reducing the terminal time $T$ as a function of $R$ and error tolerance $\varepsilon>0$. Motivated by data distributions arising in generative modelling, we also establish a cut-off like phenomenon (as $R\to\infty$) for the convergence to its invariant measure in TV of an OU process, initialized at a multi-modal distribution with maximal mode distance $R$.