Multi-Center Fetal Brain Tissue Annotation (FeTA) Challenge 2022 Results

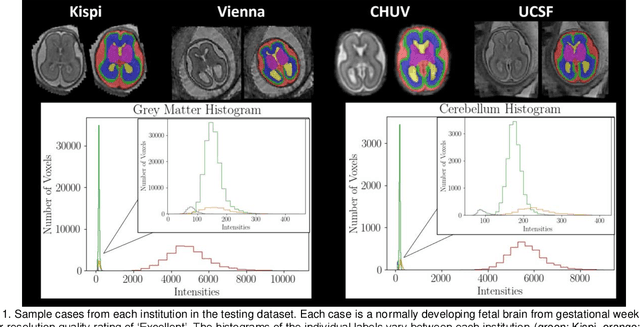
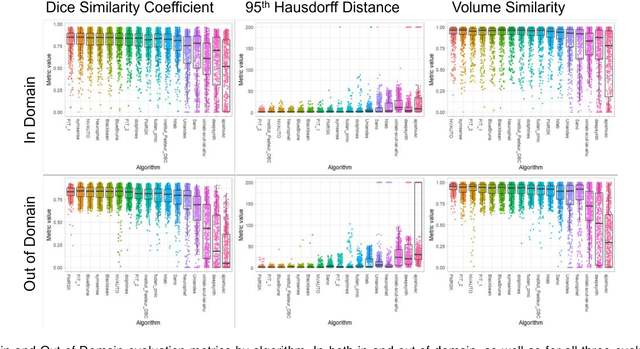
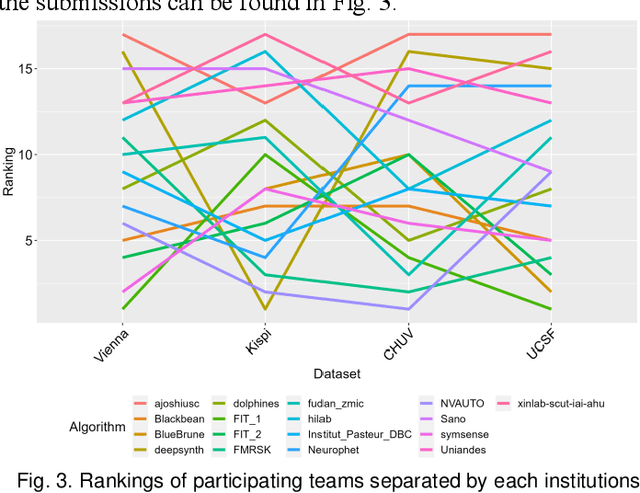
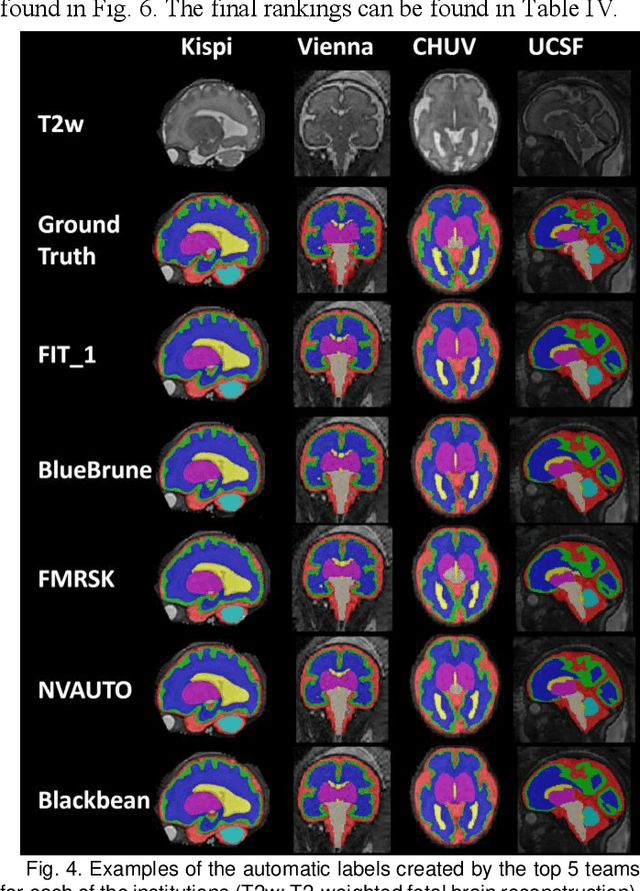
Segmentation is a critical step in analyzing the developing human fetal brain. There have been vast improvements in automatic segmentation methods in the past several years, and the Fetal Brain Tissue Annotation (FeTA) Challenge 2021 helped to establish an excellent standard of fetal brain segmentation. However, FeTA 2021 was a single center study, and the generalizability of algorithms across different imaging centers remains unsolved, limiting real-world clinical applicability. The multi-center FeTA Challenge 2022 focuses on advancing the generalizability of fetal brain segmentation algorithms for magnetic resonance imaging (MRI). In FeTA 2022, the training dataset contained images and corresponding manually annotated multi-class labels from two imaging centers, and the testing data contained images from these two imaging centers as well as two additional unseen centers. The data from different centers varied in many aspects, including scanners used, imaging parameters, and fetal brain super-resolution algorithms applied. 16 teams participated in the challenge, and 17 algorithms were evaluated. Here, a detailed overview and analysis of the challenge results are provided, focusing on the generalizability of the submissions. Both in- and out of domain, the white matter and ventricles were segmented with the highest accuracy, while the most challenging structure remains the cerebral cortex due to anatomical complexity. The FeTA Challenge 2022 was able to successfully evaluate and advance generalizability of multi-class fetal brain tissue segmentation algorithms for MRI and it continues to benchmark new algorithms. The resulting new methods contribute to improving the analysis of brain development in utero.

Approximate information maximization for bandit games

Entropy maximization and free energy minimization are general physical principles for modeling the dynamics of various physical systems. Notable examples include modeling decision-making within the brain using the free-energy principle, optimizing the accuracy-complexity trade-off when accessing hidden variables with the information bottleneck principle (Tishby et al., 2000), and navigation in random environments using information maximization (Vergassola et al., 2007). Built on this principle, we propose a new class of bandit algorithms that maximize an approximation to the information of a key variable within the system. To this end, we develop an approximated analytical physics-based representation of an entropy to forecast the information gain of each action and greedily choose the one with the largest information gain. This method yields strong performances in classical bandit settings. Motivated by its empirical success, we prove its asymptotic optimality for the two-armed bandit problem with Gaussian rewards. Owing to its ability to encompass the system's properties in a global physical functional, this approach can be efficiently adapted to more complex bandit settings, calling for further investigation of information maximization approaches for multi-armed bandit problems.

Approximate information for efficient exploration-exploitation strategies

This paper addresses the exploration-exploitation dilemma inherent in decision-making, focusing on multi-armed bandit problems. The problems involve an agent deciding whether to exploit current knowledge for immediate gains or explore new avenues for potential long-term rewards. We here introduce a novel algorithm, approximate information maximization (AIM), which employs an analytical approximation of the entropy gradient to choose which arm to pull at each point in time. AIM matches the performance of Infomax and Thompson sampling while also offering enhanced computational speed, determinism, and tractability. Empirical evaluation of AIM indicates its compliance with the Lai-Robbins asymptotic bound and demonstrates its robustness for a range of priors. Its expression is tunable, which allows for specific optimization in various settings.

Amortised inference of fractional Brownian motion with linear computational complexity

We introduce a simulation-based, amortised Bayesian inference scheme to infer the parameters of random walks. Our approach learns the posterior distribution of the walks' parameters with a likelihood-free method. In the first step a graph neural network is trained on simulated data to learn optimized low-dimensional summary statistics of the random walk. In the second step an invertible neural network generates the posterior distribution of the parameters from the learnt summary statistics using variational inference. We apply our method to infer the parameters of the fractional Brownian motion model from single trajectories. The computational complexity of the amortized inference procedure scales linearly with trajectory length, and its precision scales similarly to the Cram{\'e}r-Rao bound over a wide range of lengths. The approach is robust to positional noise, and generalizes well to trajectories longer than those seen during training. Finally, we adapt this scheme to show that a finite decorrelation time in the environment can furthermore be inferred from individual trajectories.

Learning physical properties of anomalous random walks using graph neural networks

Single particle tracking allows probing how biomolecules interact physically with their natural environments. A fundamental challenge when analysing recorded single particle trajectories is the inverse problem of inferring the physical model or class of models of the underlying random walks. Reliable inference is made difficult by the inherent stochastic nature of single particle motion, by experimental noise, and by the short duration of most experimental trajectories. Model identification is further complicated by the fact that main physical properties of random walk models are only defined asymptotically, and are thus degenerate for short trajectories. Here, we introduce a new, fast approach to inferring random walk properties based on graph neural networks (GNNs). Our approach consists in associating a vector of features with each observed position, and a sparse graph structure with each observed trajectory. By performing simulation-based supervised learning on this construct [1], we show that we can reliably learn models of random walks and their anomalous exponents. The method can naturally be applied to trajectories of any length. We show its efficiency in analysing various anomalous random walks of biological relevance that were proposed in the AnDi challenge [2]. We explore how information is encoded in the GNN, and we show that it learns relevant physical features of the random walks. We furthermore evaluate its ability to generalize to types of trajectories not seen during training, and we show that the GNN retains high accuracy even with few parameters. We finally discuss the possibility to leverage these networks to analyse experimental data.