Russell Tsuchida
Open Set Label Shift with Test Time Out-of-Distribution Reference
May 09, 2025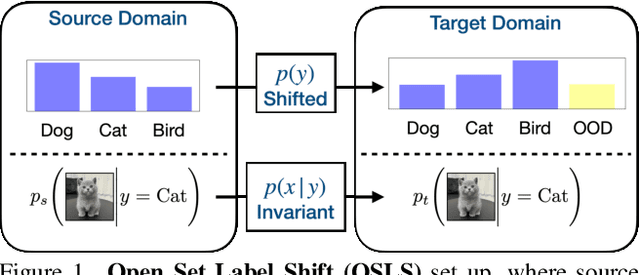
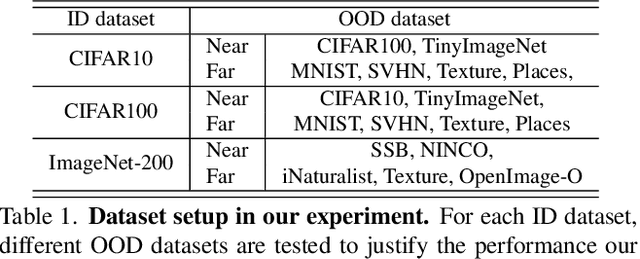
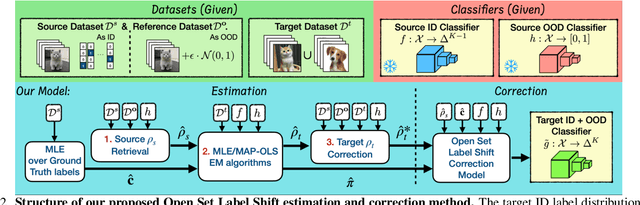

Abstract:Open set label shift (OSLS) occurs when label distributions change from a source to a target distribution, and the target distribution has an additional out-of-distribution (OOD) class. In this work, we build estimators for both source and target open set label distributions using a source domain in-distribution (ID) classifier and an ID/OOD classifier. With reasonable assumptions on the ID/OOD classifier, the estimators are assembled into a sequence of three stages: 1) an estimate of the source label distribution of the OOD class, 2) an EM algorithm for Maximum Likelihood estimates (MLE) of the target label distribution, and 3) an estimate of the target label distribution of OOD class under relaxed assumptions on the OOD classifier. The sampling errors of estimates in 1) and 3) are quantified with a concentration inequality. The estimation result allows us to correct the ID classifier trained on the source distribution to the target distribution without retraining. Experiments on a variety of open set label shift settings demonstrate the effectiveness of our model. Our code is available at https://github.com/ChangkunYe/OpenSetLabelShift.
Squared families: Searching beyond regular probability models
Mar 27, 2025
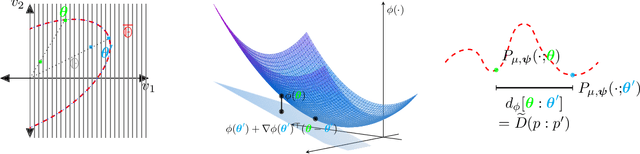
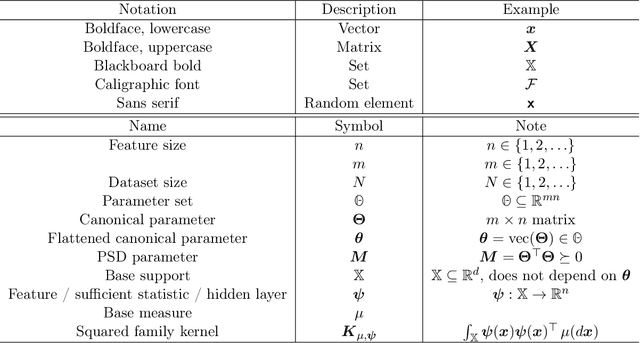
Abstract:We introduce squared families, which are families of probability densities obtained by squaring a linear transformation of a statistic. Squared families are singular, however their singularity can easily be handled so that they form regular models. After handling the singularity, squared families possess many convenient properties. Their Fisher information is a conformal transformation of the Hessian metric induced from a Bregman generator. The Bregman generator is the normalising constant, and yields a statistical divergence on the family. The normalising constant admits a helpful parameter-integral factorisation, meaning that only one parameter-independent integral needs to be computed for all normalising constants in the family, unlike in exponential families. Finally, the squared family kernel is the only integral that needs to be computed for the Fisher information, statistical divergence and normalising constant. We then describe how squared families are special in the broader class of $g$-families, which are obtained by applying a sufficiently regular function $g$ to a linear transformation of a statistic. After removing special singularities, positively homogeneous families and exponential families are the only $g$-families for which the Fisher information is a conformal transformation of the Hessian metric, where the generator depends on the parameter only through the normalising constant. Even-order monomial families also admit parameter-integral factorisations, unlike exponential families. We study parameter estimation and density estimation in squared families, in the well-specified and misspecified settings. We use a universal approximation property to show that squared families can learn sufficiently well-behaved target densities at a rate of $\mathcal{O}(N^{-1/2})+C n^{-1/4}$, where $N$ is the number of datapoints, $n$ is the number of parameters, and $C$ is some constant.
Generalization Certificates for Adversarially Robust Bayesian Linear Regression
Feb 20, 2025
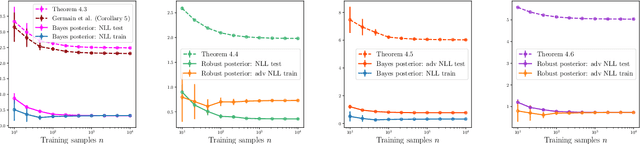
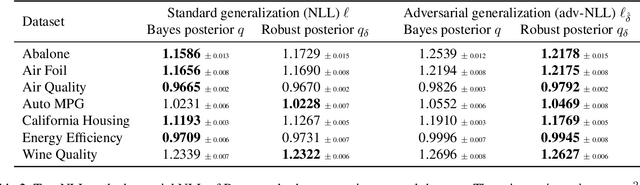
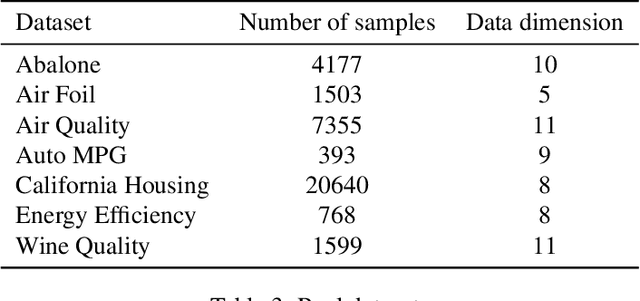
Abstract:Adversarial robustness of machine learning models is critical to ensuring reliable performance under data perturbations. Recent progress has been on point estimators, and this paper considers distributional predictors. First, using the link between exponential families and Bregman divergences, we formulate an adversarial Bregman divergence loss as an adversarial negative log-likelihood. Using the geometric properties of Bregman divergences, we compute the adversarial perturbation for such models in closed-form. Second, under such losses, we introduce \emph{adversarially robust posteriors}, by exploiting the optimization-centric view of generalized Bayesian inference. Third, we derive the \emph{first} rigorous generalization certificates in the context of an adversarial extension of Bayesian linear regression by leveraging the PAC-Bayesian framework. Finally, experiments on real and synthetic datasets demonstrate the superior robustness of the derived adversarially robust posterior over Bayes posterior, and also validate our theoretical guarantees.
Label Distribution Learning using the Squared Neural Family on the Probability Simplex
Dec 10, 2024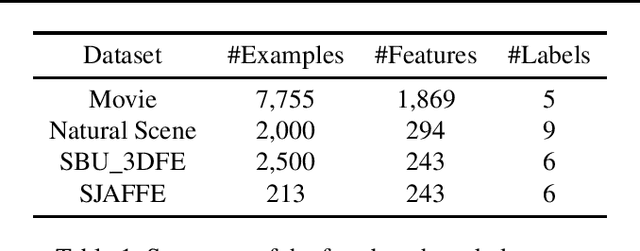
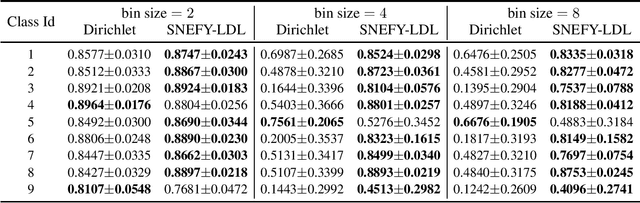
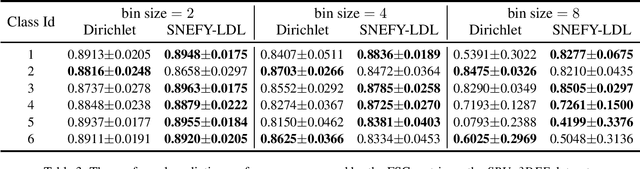
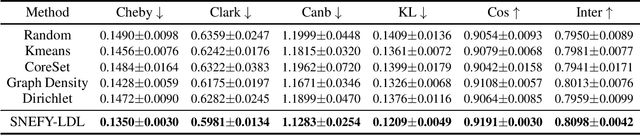
Abstract:Label distribution learning (LDL) provides a framework wherein a distribution over categories rather than a single category is predicted, with the aim of addressing ambiguity in labeled data. Existing research on LDL mainly focuses on the task of point estimation, i.e., pinpointing an optimal distribution in the probability simplex conditioned on the input sample. In this paper, we estimate a probability distribution of all possible label distributions over the simplex, by unleashing the expressive power of the recently introduced Squared Neural Family (SNEFY). With the modeled distribution, label distribution prediction can be achieved by performing the expectation operation to estimate the mean of the distribution of label distributions. Moreover, more information about the label distribution can be inferred, such as the prediction reliability and uncertainties. We conduct extensive experiments on the label distribution prediction task, showing that our distribution modeling based method can achieve very competitive label distribution prediction performance compared with the state-of-the-art baselines. Additional experiments on active learning and ensemble learning demonstrate that our probabilistic approach can effectively boost the performance in these settings, by accurately estimating the prediction reliability and uncertainties.
Exact, Fast and Expressive Poisson Point Processes via Squared Neural Families
Feb 14, 2024Abstract:We introduce squared neural Poisson point processes (SNEPPPs) by parameterising the intensity function by the squared norm of a two layer neural network. When the hidden layer is fixed and the second layer has a single neuron, our approach resembles previous uses of squared Gaussian process or kernel methods, but allowing the hidden layer to be learnt allows for additional flexibility. In many cases of interest, the integrated intensity function admits a closed form and can be computed in quadratic time in the number of hidden neurons. We enumerate a far more extensive number of such cases than has previously been discussed. Our approach is more memory and time efficient than naive implementations of squared or exponentiated kernel methods or Gaussian processes. Maximum likelihood and maximum a posteriori estimates in a reparameterisation of the final layer of the intensity function can be obtained by solving a (strongly) convex optimisation problem using projected gradient descent. We demonstrate SNEPPPs on real, and synthetic benchmarks, and provide a software implementation. https://github.com/RussellTsuchida/snefy
Gaussian Ensemble Belief Propagation for Efficient Inference in High-Dimensional Systems
Feb 13, 2024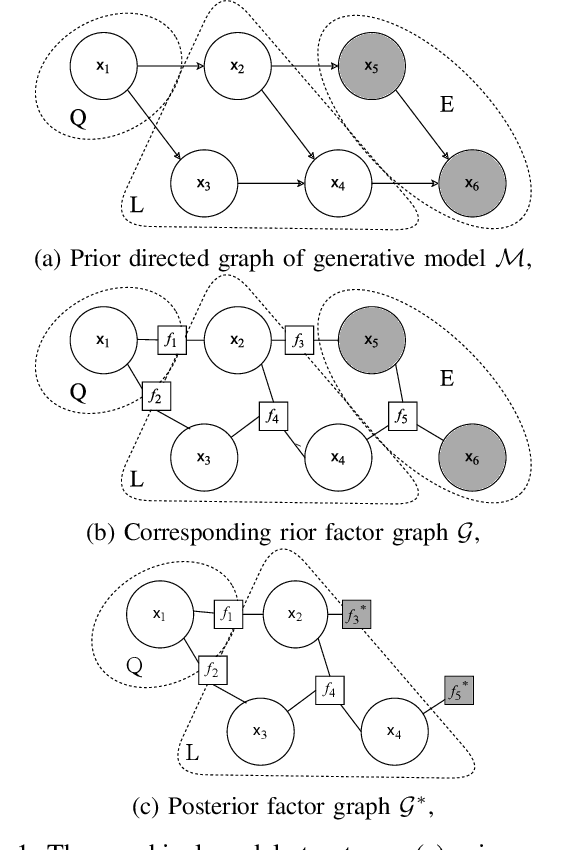
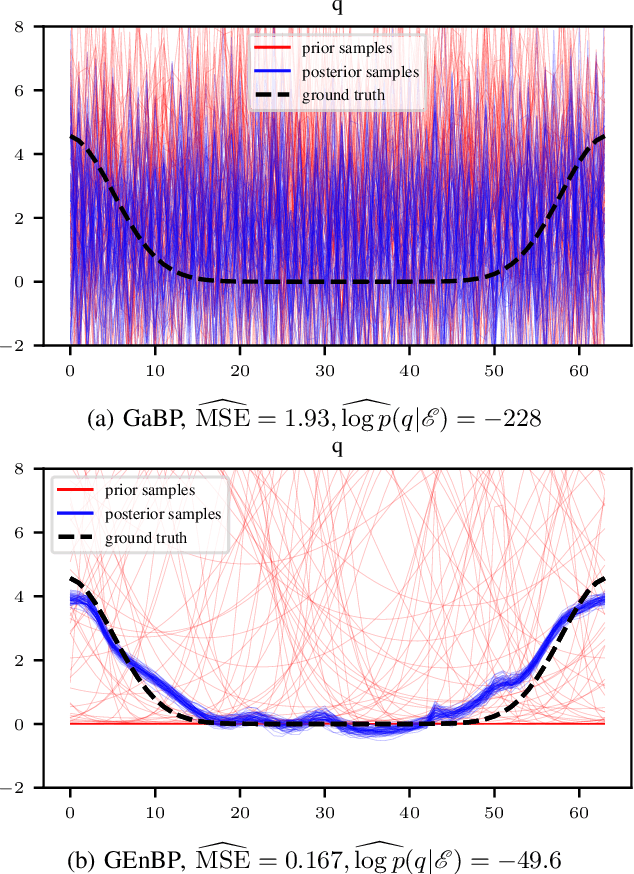
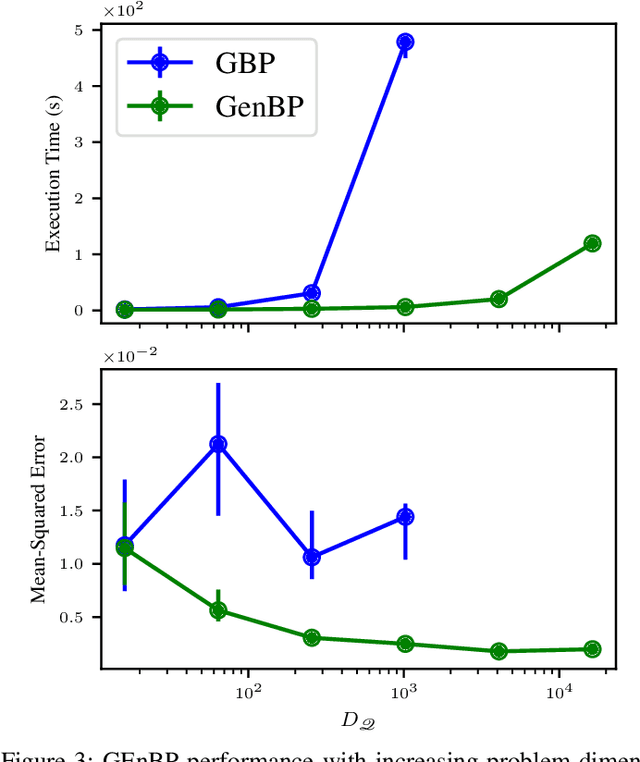
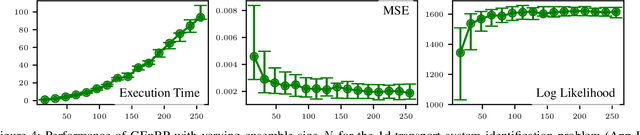
Abstract:Efficient inference in high-dimensional models remains a central challenge in machine learning. This paper introduces the Gaussian Ensemble Belief Propagation (GEnBP) algorithm, a fusion of the Ensemble Kalman filter and Gaussian belief propagation (GaBP) methods. GEnBP updates ensembles by passing low-rank local messages in a graphical model structure. This combination inherits favourable qualities from each method. Ensemble techniques allow GEnBP to handle high-dimensional states, parameters and intricate, noisy, black-box generation processes. The use of local messages in a graphical model structure ensures that the approach is suited to distributed computing and can efficiently handle complex dependence structures. GEnBP is particularly advantageous when the ensemble size is considerably smaller than the inference dimension. This scenario often arises in fields such as spatiotemporal modelling, image processing and physical model inversion. GEnBP can be applied to general problem structures, including jointly learning system parameters, observation parameters, and latent state variables.
Squared Neural Families: A New Class of Tractable Density Models
May 22, 2023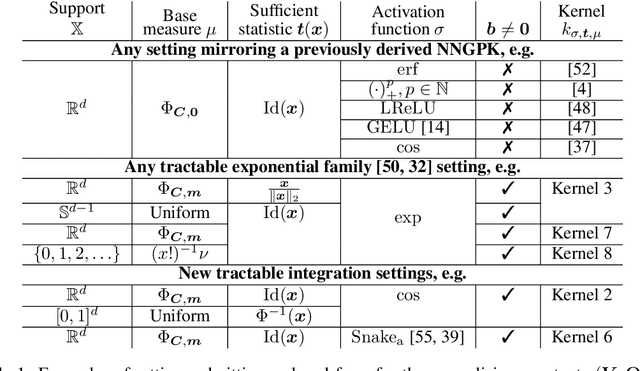
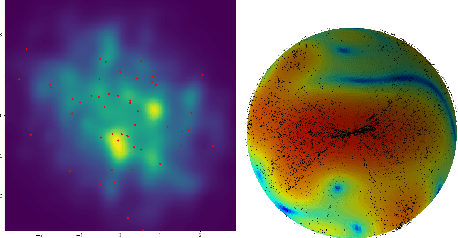

Abstract:Flexible models for probability distributions are an essential ingredient in many machine learning tasks. We develop and investigate a new class of probability distributions, which we call a Squared Neural Family (SNEFY), formed by squaring the 2-norm of a neural network and normalising it with respect to a base measure. Following the reasoning similar to the well established connections between infinitely wide neural networks and Gaussian processes, we show that SNEFYs admit a closed form normalising constants in many cases of interest, thereby resulting in flexible yet fully tractable density models. SNEFYs strictly generalise classical exponential families, are closed under conditioning, and have tractable marginal distributions. Their utility is illustrated on a variety of density estimation and conditional density estimation tasks. Software available at https://github.com/RussellTsuchida/snefy.
Earth Movers in The Big Data Era: A Review of Optimal Transport in Machine Learning
May 08, 2023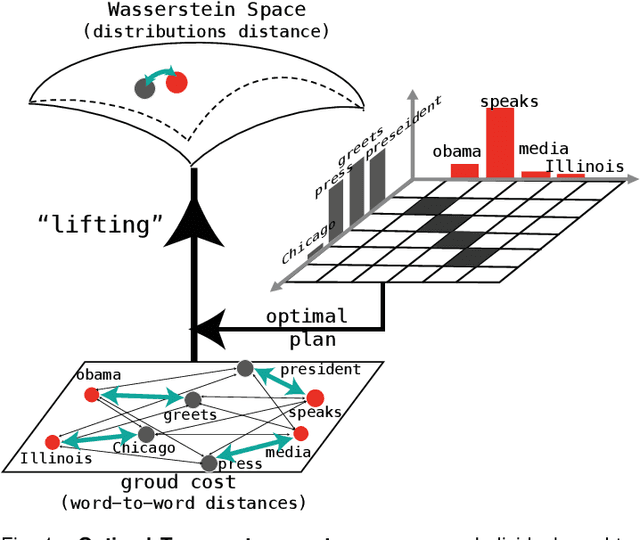
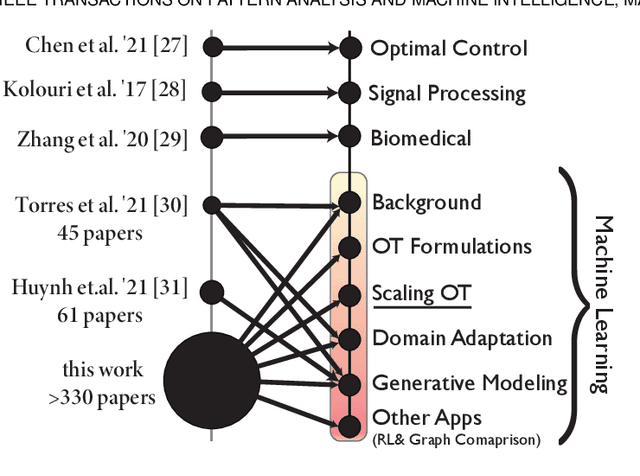
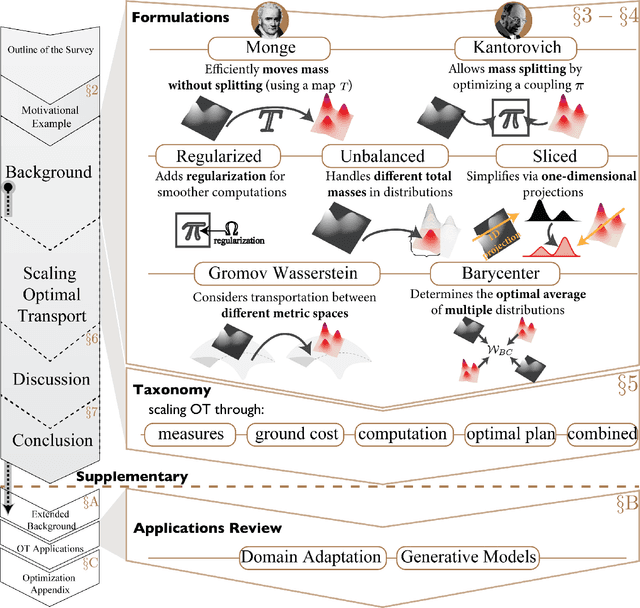
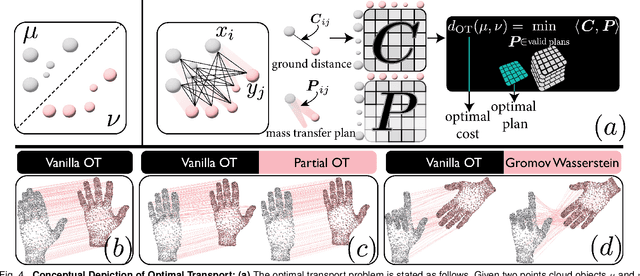
Abstract:Optimal Transport (OT) is a mathematical framework that first emerged in the eighteenth century and has led to a plethora of methods for answering many theoretical and applied questions. The last decade is a witness of the remarkable contributions of this classical optimization problem to machine learning. This paper is about where and how optimal transport is used in machine learning with a focus on the question of salable optimal transport. We provide a comprehensive survey of optimal transport while ensuring an accessible presentation as permitted by the nature of the topic and the context. First, we explain optimal transport background and introduce different flavors (i.e. mathematical formulations), properties, and notable applications. We then address the fundamental question of how to scale optimal transport to cope with the current demands of big and high dimensional data. We conduct a systematic analysis of the methods used in the literature for scaling OT and present the findings in a unified taxonomy. We conclude with presenting some open challenges and discussing potential future research directions. A live repository of related OT research papers is maintained in https://github.com/abdelwahed/OT_for_big_data.git.
Deep equilibrium models as estimators for continuous latent variables
Nov 11, 2022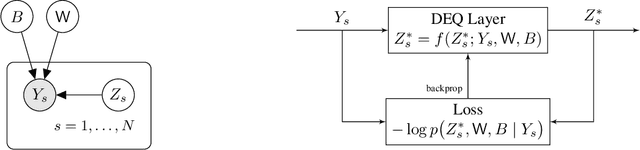
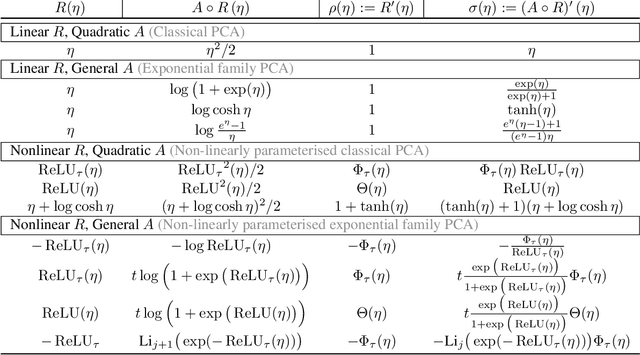
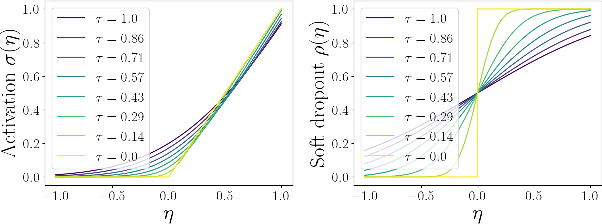
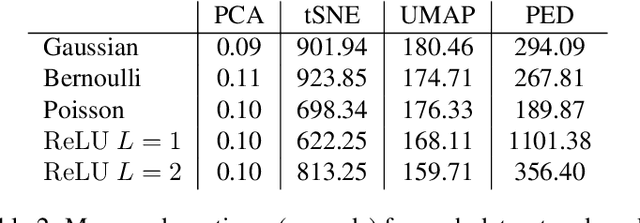
Abstract:Principal Component Analysis (PCA) and its exponential family extensions have three components: observations, latents and parameters of a linear transformation. We consider a generalised setting where the canonical parameters of the exponential family are a nonlinear transformation of the latents. We show explicit relationships between particular neural network architectures and the corresponding statistical models. We find that deep equilibrium models -- a recently introduced class of implicit neural networks -- solve maximum a-posteriori (MAP) estimates for the latents and parameters of the transformation. Our analysis provides a systematic way to relate activation functions, dropout, and layer structure, to statistical assumptions about the observations, thus providing foundational principles for unsupervised DEQs. For hierarchical latents, individual neurons can be interpreted as nodes in a deep graphical model. Our DEQ feature maps are end-to-end differentiable, enabling fine-tuning for downstream tasks.
Efficient Gaussian Process Model on Class-Imbalanced Datasets for Generalized Zero-Shot Learning
Oct 11, 2022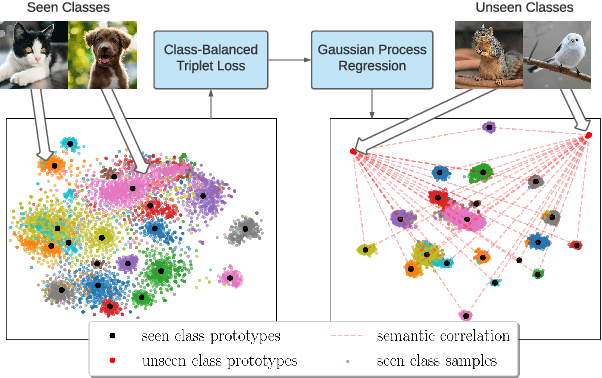
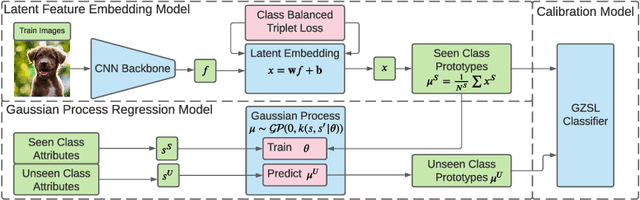
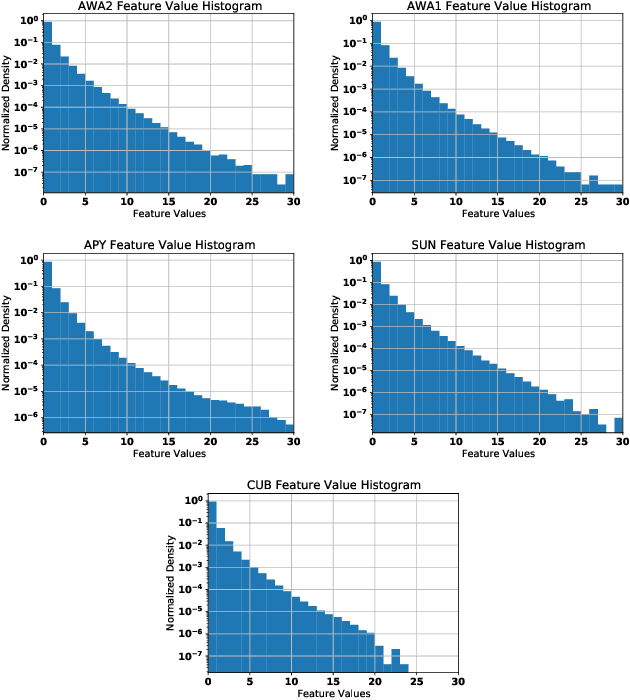
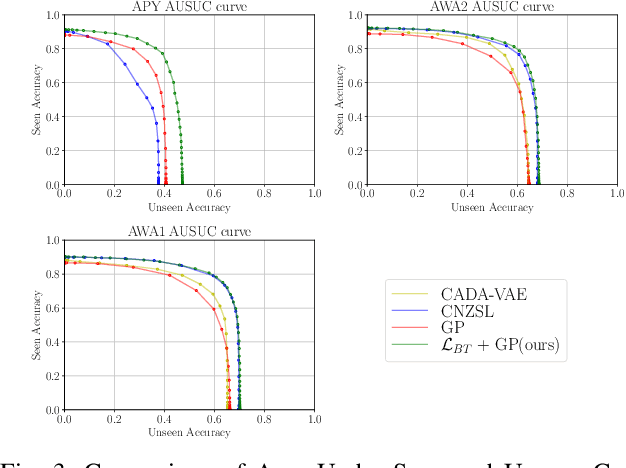
Abstract:Zero-Shot Learning (ZSL) models aim to classify object classes that are not seen during the training process. However, the problem of class imbalance is rarely discussed, despite its presence in several ZSL datasets. In this paper, we propose a Neural Network model that learns a latent feature embedding and a Gaussian Process (GP) regression model that predicts latent feature prototypes of unseen classes. A calibrated classifier is then constructed for ZSL and Generalized ZSL tasks. Our Neural Network model is trained efficiently with a simple training strategy that mitigates the impact of class-imbalanced training data. The model has an average training time of 5 minutes and can achieve state-of-the-art (SOTA) performance on imbalanced ZSL benchmark datasets like AWA2, AWA1 and APY, while having relatively good performance on the SUN and CUB datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge