Gaussian Ensemble Belief Propagation for Efficient Inference in High-Dimensional Systems

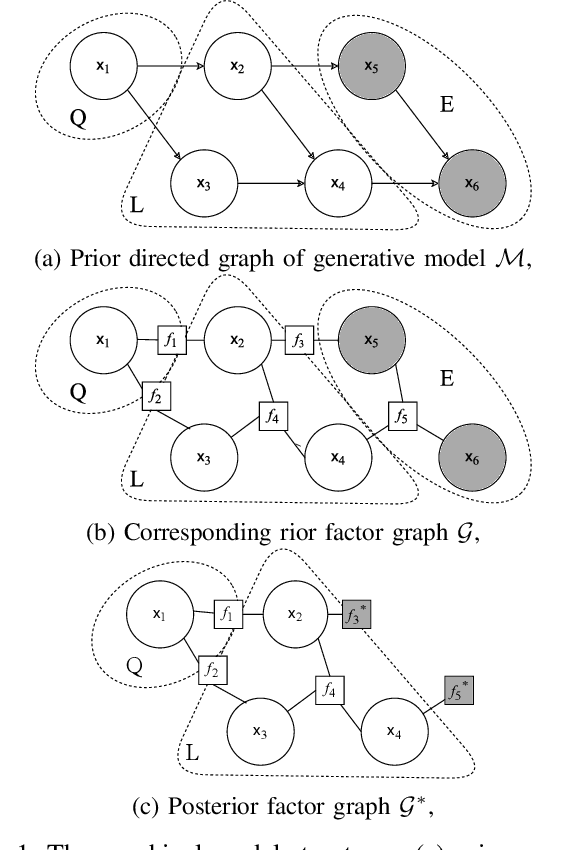
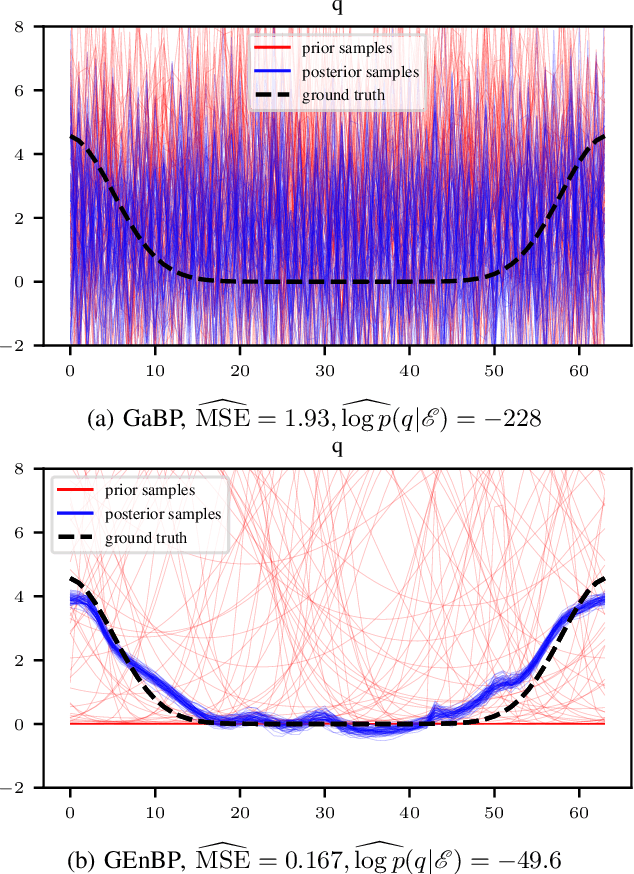
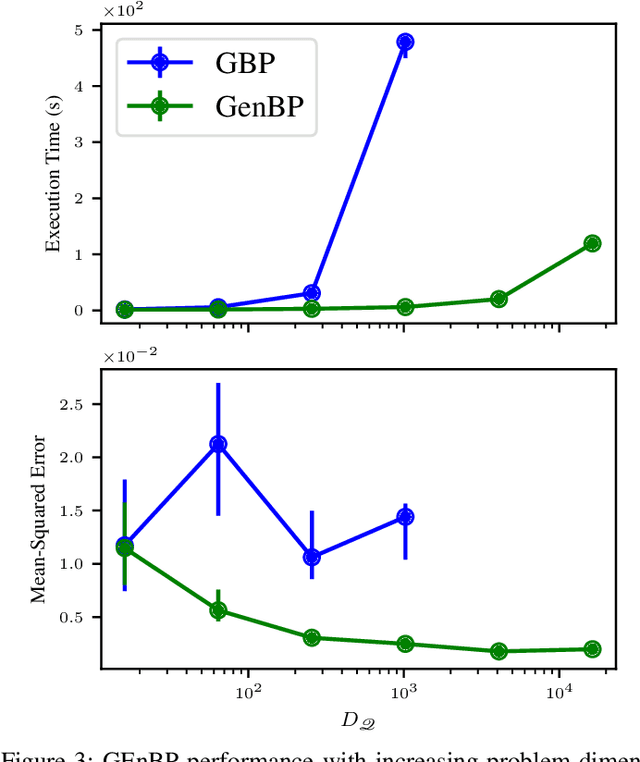
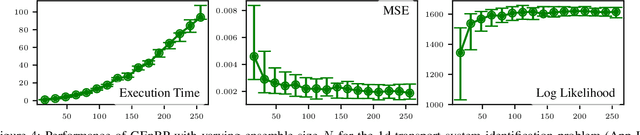
Efficient inference in high-dimensional models remains a central challenge in machine learning. This paper introduces the Gaussian Ensemble Belief Propagation (GEnBP) algorithm, a fusion of the Ensemble Kalman filter and Gaussian belief propagation (GaBP) methods. GEnBP updates ensembles by passing low-rank local messages in a graphical model structure. This combination inherits favourable qualities from each method. Ensemble techniques allow GEnBP to handle high-dimensional states, parameters and intricate, noisy, black-box generation processes. The use of local messages in a graphical model structure ensures that the approach is suited to distributed computing and can efficiently handle complex dependence structures. GEnBP is particularly advantageous when the ensemble size is considerably smaller than the inference dimension. This scenario often arises in fields such as spatiotemporal modelling, image processing and physical model inversion. GEnBP can be applied to general problem structures, including jointly learning system parameters, observation parameters, and latent state variables.

Resolving Ethics Trade-offs in Implementing Responsible AI

While the operationalisation of high-level AI ethics principles into practical AI/ML systems has made progress, there is still a theory-practice gap in managing tensions between the underlying AI ethics aspects. We cover five approaches for addressing the tensions via trade-offs, ranging from rudimentary to complex. The approaches differ in the types of considered context, scope, methods for measuring contexts, and degree of justification. None of the approaches is likely to be appropriate for all organisations, systems, or applications. To address this, we propose a framework which consists of: (i) proactive identification of tensions, (ii) prioritisation and weighting of ethics aspects, (iii) justification and documentation of trade-off decisions. The proposed framework aims to facilitate the implementation of well-rounded AI/ML systems that are appropriate for potential regulatory requirements.

A Neural Emulator for Uncertainty Estimation of Fire Propagation

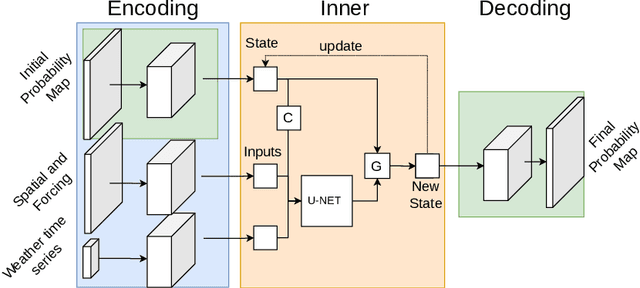
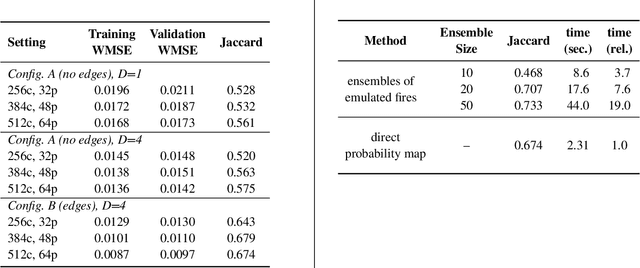
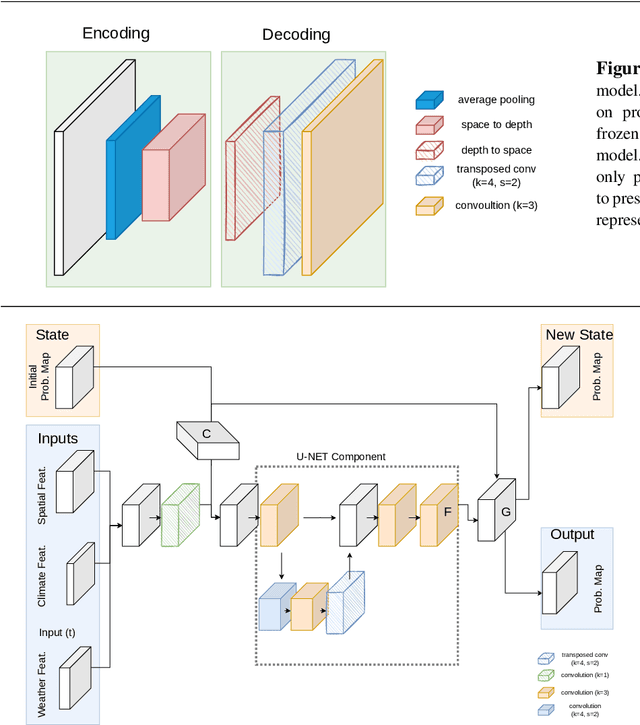
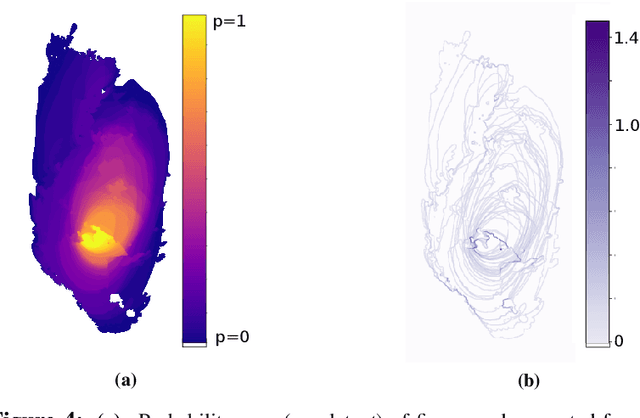
Wildfire propagation is a highly stochastic process where small changes in environmental conditions (such as wind speed and direction) can lead to large changes in observed behaviour. A traditional approach to quantify uncertainty in fire-front progression is to generate probability maps via ensembles of simulations. However, use of ensembles is typically computationally expensive, which can limit the scope of uncertainty analysis. To address this, we explore the use of a spatio-temporal neural-based modelling approach to directly estimate the likelihood of fire propagation given uncertainty in input parameters. The uncertainty is represented by deliberately perturbing the input weather forecast during model training. The computational load is concentrated in the model training process, which allows larger probability spaces to be explored during deployment. Empirical evaluations indicate that the proposed model achieves comparable fire boundaries to those produced by the traditional SPARK simulation platform, with an overall Jaccard index (similarity score) of 67.4% on a set of 35 simulated fires. When compared to a related neural model (emulator) which was employed to generate probability maps via ensembles of emulated fires, the proposed approach produces competitive Jaccard similarity scores while being approximately an order of magnitude faster.

Bayesian Physics Informed Neural Networks for Data Assimilation and Spatio-Temporal Modelling of Wildfires

We apply Physics Informed Neural Networks (PINNs) to the problem of wildfire fire-front modelling. The PINN is an approach that integrates a differential equation into the optimisation loss function of a neural network to guide the neural network to learn the physics of a problem. We apply the PINN to the level-set equation, which is a Hamilton-Jacobi partial differential equation that models a fire-front with the zero-level set. This results in a PINN that simulates a fire-front as it propagates through a spatio-temporal domain. We demonstrate the agility of the PINN to learn physical properties of a fire under extreme changes in external conditions (such as wind) and show that this approach encourages continuity of the PINN's solution across time. Furthermore, we demonstrate how data assimilation and uncertainty quantification can be incorporated into the PINN in the wildfire context. This is significant contribution to wildfire modelling as the level-set method -- which is a standard solver to the level-set equation -- does not naturally provide this capability.

A Spatio-Temporal Neural Network Forecasting Approach for Emulation of Firefront Models

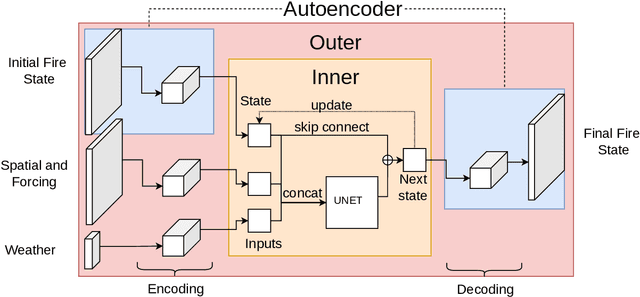
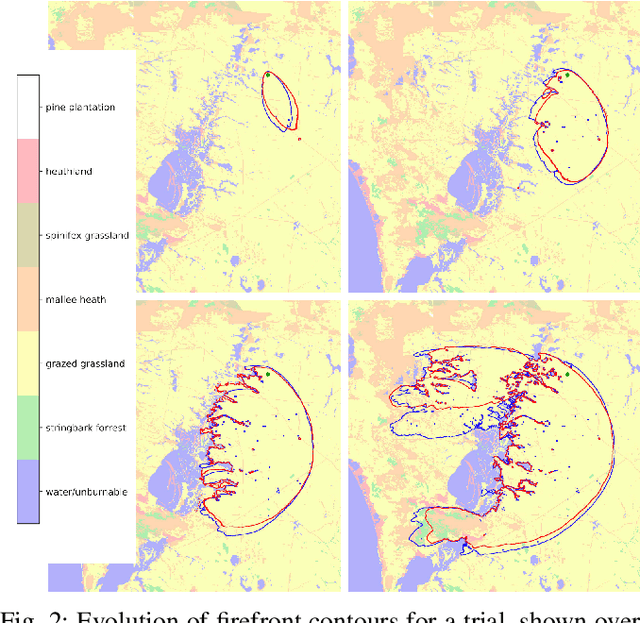
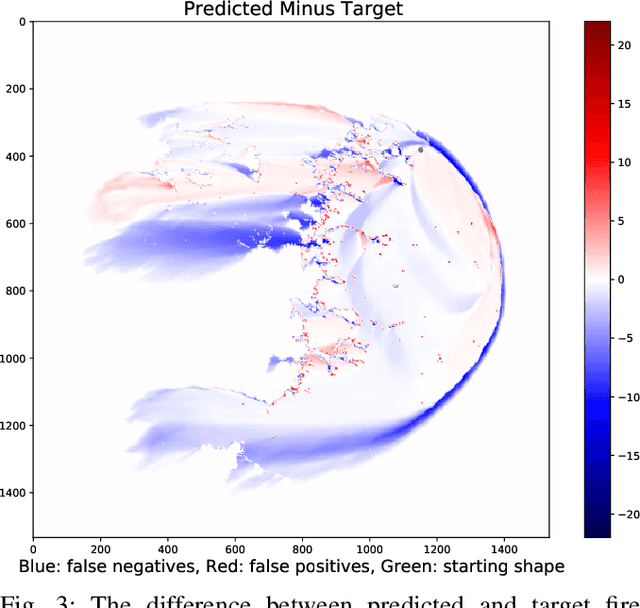
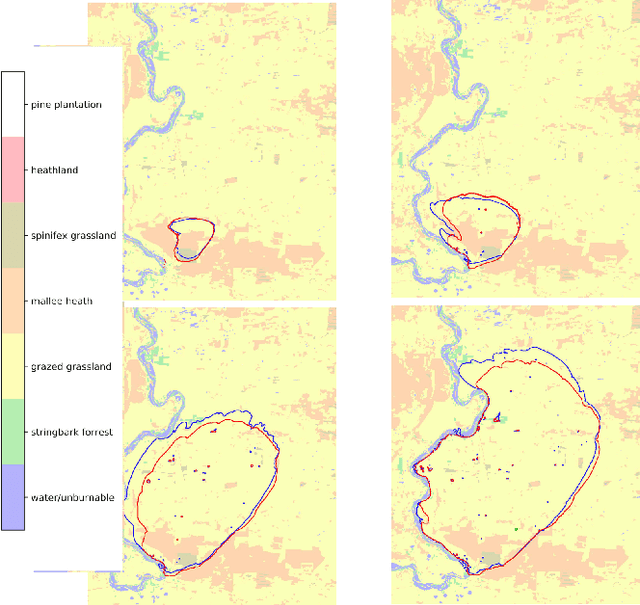
Computational simulations of wildfire spread typically employ empirical rate-of-spread calculations under various conditions (such as terrain, fuel type, weather). Small perturbations in conditions can often lead to significant changes in fire spread (such as speed and direction), necessitating a computationally expensive large set of simulations to quantify uncertainty. Model emulation seeks alternative representations of physical models using machine learning, aiming to provide more efficient and/or simplified surrogate models. We propose a dedicated spatio-temporal neural network based framework for model emulation, able to capture the complex behaviour of fire spread models. The proposed approach can approximate forecasts at fine spatial and temporal resolutions that are often challenging for neural network based approaches. Furthermore, the proposed approach is robust even with small training sets, due to novel data augmentation methods. Empirical experiments show good agreement between simulated and emulated firefronts, with an average Jaccard score of 0.76.

An Emulation Framework for Fire Front Spread

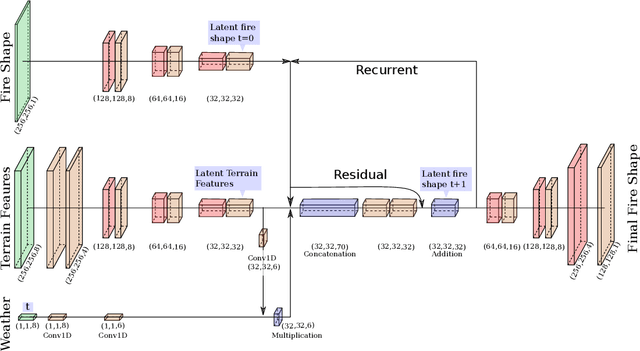
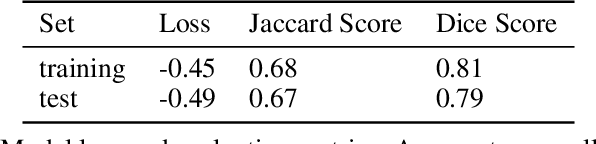
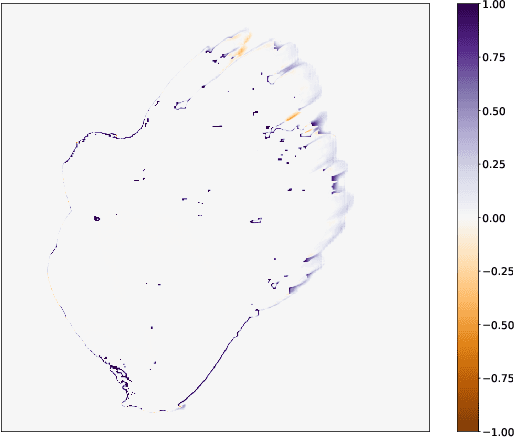
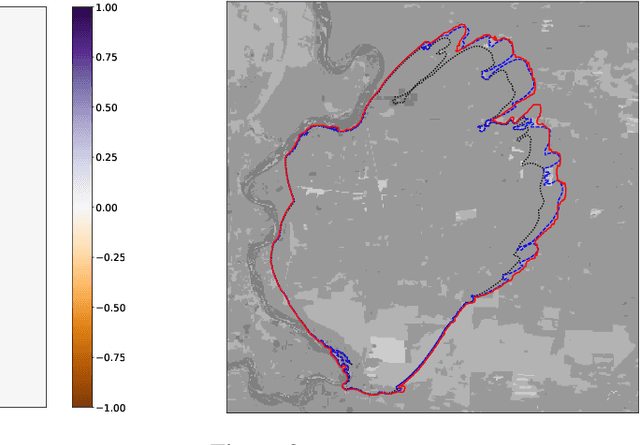
Forecasting bushfire spread is an important element in fire prevention and response efforts. Empirical observations of bushfire spread can be used to estimate fire response under certain conditions. These observations form rate-of-spread models, which can be used to generate simulations. We use machine learning to drive the emulation approach for bushfires and show that emulation has the capacity to closely reproduce simulated fire-front data. We present a preliminary emulator approach with the capacity for fast emulation of complex simulations. Large numbers of predictions can then be generated as part of ensemble estimation techniques, which provide more robust and reliable forecasts of stochastic systems.