Exploiting Field Dependencies for Learning on Categorical Data

Traditional approaches for learning on categorical data underexploit the dependencies between columns (\aka fields) in a dataset because they rely on the embedding of data points driven alone by the classification/regression loss. In contrast, we propose a novel method for learning on categorical data with the goal of exploiting dependencies between fields. Instead of modelling statistics of features globally (i.e., by the covariance matrix of features), we learn a global field dependency matrix that captures dependencies between fields and then we refine the global field dependency matrix at the instance-wise level with different weights (so-called local dependency modelling) w.r.t. each field to improve the modelling of the field dependencies. Our algorithm exploits the meta-learning paradigm, i.e., the dependency matrices are refined in the inner loop of the meta-learning algorithm without the use of labels, whereas the outer loop intertwines the updates of the embedding matrix (the matrix performing projection) and global dependency matrix in a supervised fashion (with the use of labels). Our method is simple yet it outperforms several state-of-the-art methods on six popular dataset benchmarks. Detailed ablation studies provide additional insights into our method.

Bayesian Physics Informed Neural Networks for Data Assimilation and Spatio-Temporal Modelling of Wildfires

We apply Physics Informed Neural Networks (PINNs) to the problem of wildfire fire-front modelling. The PINN is an approach that integrates a differential equation into the optimisation loss function of a neural network to guide the neural network to learn the physics of a problem. We apply the PINN to the level-set equation, which is a Hamilton-Jacobi partial differential equation that models a fire-front with the zero-level set. This results in a PINN that simulates a fire-front as it propagates through a spatio-temporal domain. We demonstrate the agility of the PINN to learn physical properties of a fire under extreme changes in external conditions (such as wind) and show that this approach encourages continuity of the PINN's solution across time. Furthermore, we demonstrate how data assimilation and uncertainty quantification can be incorporated into the PINN in the wildfire context. This is significant contribution to wildfire modelling as the level-set method -- which is a standard solver to the level-set equation -- does not naturally provide this capability.

Bayesian Neural Network Inference via Implicit Models and the Posterior Predictive Distribution

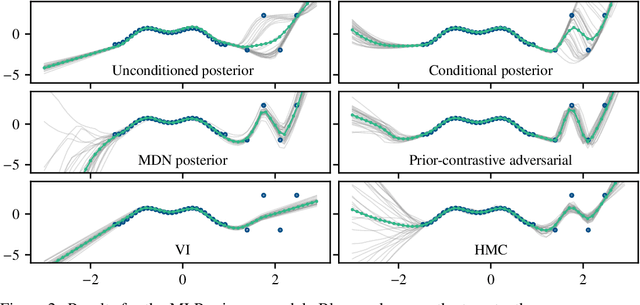
We propose a novel approach to perform approximate Bayesian inference in complex models such as Bayesian neural networks. The approach is more scalable to large data than Markov Chain Monte Carlo, it embraces more expressive models than Variational Inference, and it does not rely on adversarial training (or density ratio estimation). We adopt the recent approach of constructing two models: (1) a primary model, tasked with performing regression or classification; and (2) a secondary, expressive (e.g. implicit) model that defines an approximate posterior distribution over the parameters of the primary model. However, we optimise the parameters of the posterior model via gradient descent according to a Monte Carlo estimate of the posterior predictive distribution -- which is our only approximation (other than the posterior model). Only a likelihood needs to be specified, which can take various forms such as loss functions and synthetic likelihoods, thus providing a form of a likelihood-free approach. Furthermore, we formulate the approach such that the posterior samples can either be independent of, or conditionally dependent upon the inputs to the primary model. The latter approach is shown to be capable of increasing the apparent complexity of the primary model. We see this being useful in applications such as surrogate and physics-based models. To promote how the Bayesian paradigm offers more than just uncertainty quantification, we demonstrate: uncertainty quantification, multi-modality, as well as an application with a recent deep forecasting neural network architecture.