Bayesian Neural Network Inference via Implicit Models and the Posterior Predictive Distribution
Paper and Code
Sep 06, 2022

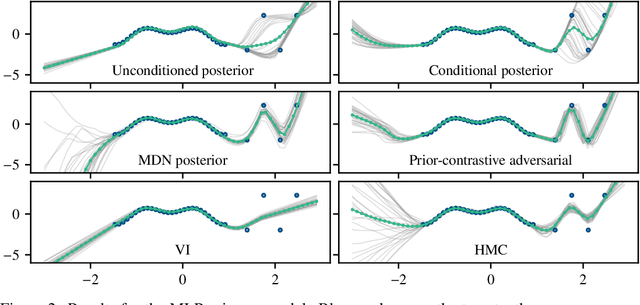

We propose a novel approach to perform approximate Bayesian inference in complex models such as Bayesian neural networks. The approach is more scalable to large data than Markov Chain Monte Carlo, it embraces more expressive models than Variational Inference, and it does not rely on adversarial training (or density ratio estimation). We adopt the recent approach of constructing two models: (1) a primary model, tasked with performing regression or classification; and (2) a secondary, expressive (e.g. implicit) model that defines an approximate posterior distribution over the parameters of the primary model. However, we optimise the parameters of the posterior model via gradient descent according to a Monte Carlo estimate of the posterior predictive distribution -- which is our only approximation (other than the posterior model). Only a likelihood needs to be specified, which can take various forms such as loss functions and synthetic likelihoods, thus providing a form of a likelihood-free approach. Furthermore, we formulate the approach such that the posterior samples can either be independent of, or conditionally dependent upon the inputs to the primary model. The latter approach is shown to be capable of increasing the apparent complexity of the primary model. We see this being useful in applications such as surrogate and physics-based models. To promote how the Bayesian paradigm offers more than just uncertainty quantification, we demonstrate: uncertainty quantification, multi-modality, as well as an application with a recent deep forecasting neural network architecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge