Deep equilibrium models as estimators for continuous latent variables
Paper and Code
Nov 11, 2022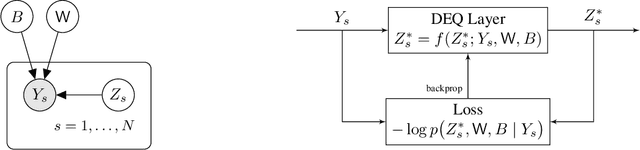
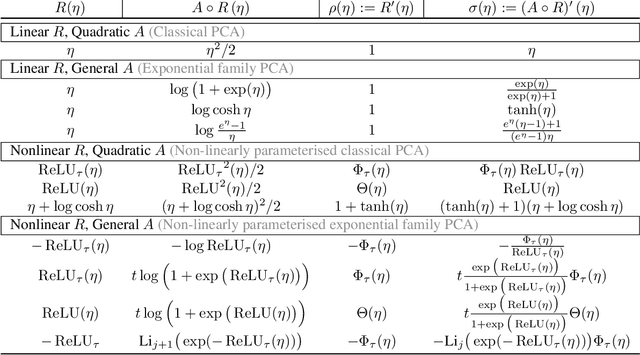
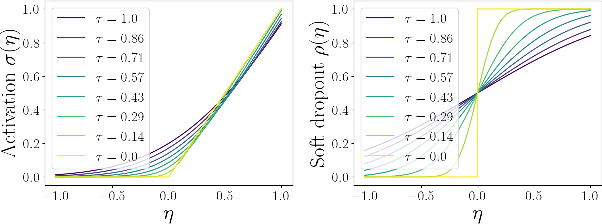
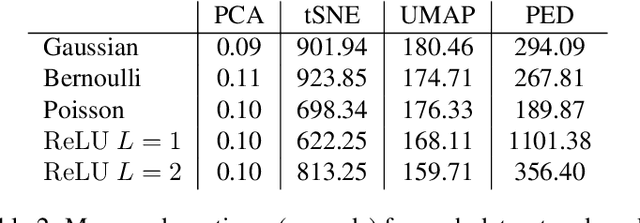
Principal Component Analysis (PCA) and its exponential family extensions have three components: observations, latents and parameters of a linear transformation. We consider a generalised setting where the canonical parameters of the exponential family are a nonlinear transformation of the latents. We show explicit relationships between particular neural network architectures and the corresponding statistical models. We find that deep equilibrium models -- a recently introduced class of implicit neural networks -- solve maximum a-posteriori (MAP) estimates for the latents and parameters of the transformation. Our analysis provides a systematic way to relate activation functions, dropout, and layer structure, to statistical assumptions about the observations, thus providing foundational principles for unsupervised DEQs. For hierarchical latents, individual neurons can be interpreted as nodes in a deep graphical model. Our DEQ feature maps are end-to-end differentiable, enabling fine-tuning for downstream tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge