Graphons of Line Graphs
Paper and Code
Sep 03, 2024
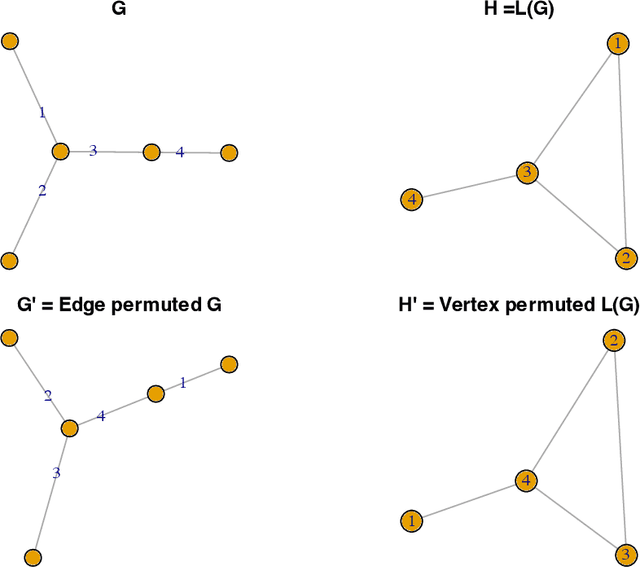
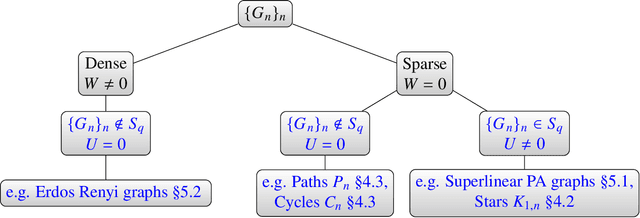
A graphon is the limit of a converging graph sequence. Graphons of dense graphs are useful as they can act as a blueprint and generate graphs of arbitrary size with similar properties. But for sparse graphs this is not the case. Sparse graphs converge to the zero graphon, making the generated graphs empty or edgeless. Thus, the classical graphon definition fails for sparse graphs. Several methods have been proposed to overcome this limitation and to understand sparse graphs more deeply. However, the fragile nature of sparse graphs makes these methods mathematically complex. In this paper we show a simple method that can shed light on a certain subset of sparse graphs. The method involves mapping the original graphs to their line graphs. Line graphs map edges to vertices and connects edges when edges in the original graph share a vertex. We show that graphs satisfying a particular property, which we call the square-degree property are sparse, but give rise to dense line graphs. In particular, star graphs satisfy the square-degree property resulting in dense line graphs and non-zero graphons of line graphs. Similarly, superlinear preferential attachment graphs give rise to dense line graphs almost surely. In contrast, dense graphs, including Erdos-Renyi graphs make the line graphs sparse, resulting in the zero graphon.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge