Indirect Query Bayesian Optimization with Integrated Feedback
Paper and Code
Dec 18, 2024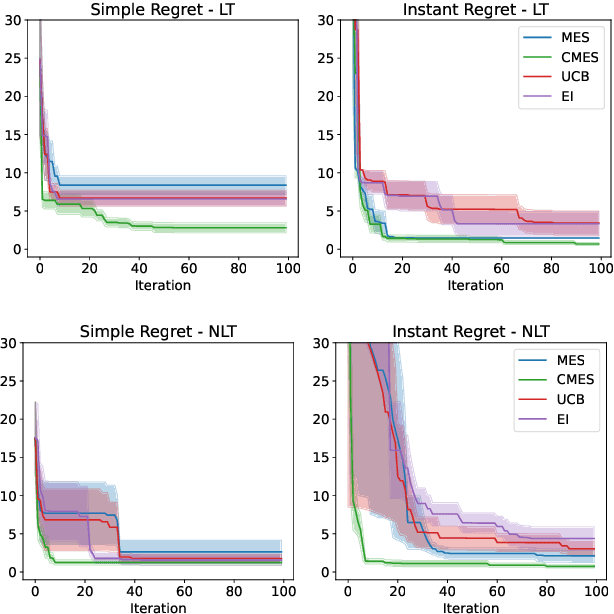

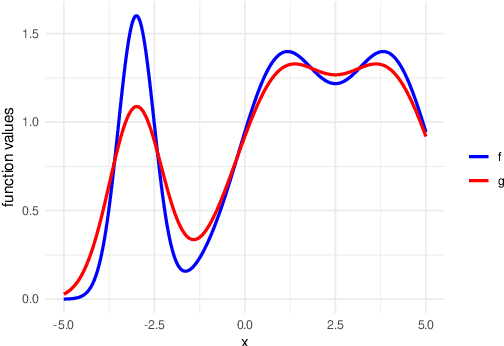
We develop the framework of Indirect Query Bayesian Optimization (IQBO), a new class of Bayesian optimization problems where the integrated feedback is given via a conditional expectation of the unknown function $f$ to be optimized. The underlying conditional distribution can be unknown and learned from data. The goal is to find the global optimum of $f$ by adaptively querying and observing in the space transformed by the conditional distribution. This is motivated by real-world applications where one cannot access direct feedback due to privacy, hardware or computational constraints. We propose the Conditional Max-Value Entropy Search (CMES) acquisition function to address this novel setting, and propose a hierarchical search algorithm to address the multi-resolution setting and improve the computational efficiency. We show regret bounds for our proposed methods and demonstrate the effectiveness of our approaches on simulated optimization tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge