Scalable Vertical Federated Learning via Data Augmentation and Amortized Inference
Paper and Code
May 07, 2024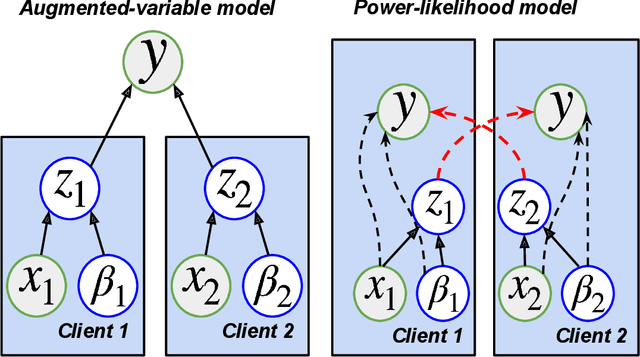


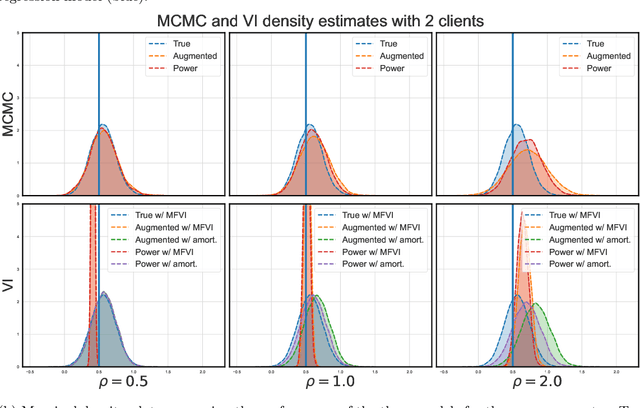
Vertical federated learning (VFL) has emerged as a paradigm for collaborative model estimation across multiple clients, each holding a distinct set of covariates. This paper introduces the first comprehensive framework for fitting Bayesian models in the VFL setting. We propose a novel approach that leverages data augmentation techniques to transform VFL problems into a form compatible with existing Bayesian federated learning algorithms. We present an innovative model formulation for specific VFL scenarios where the joint likelihood factorizes into a product of client-specific likelihoods. To mitigate the dimensionality challenge posed by data augmentation, which scales with the number of observations and clients, we develop a factorized amortized variational approximation that achieves scalability independent of the number of observations. We showcase the efficacy of our framework through extensive numerical experiments on logistic regression, multilevel regression, and a novel hierarchical Bayesian split neural net model. Our work paves the way for privacy-preserving, decentralized Bayesian inference in vertically partitioned data scenarios, opening up new avenues for research and applications in various domains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge