Scalable approximate inference for state space models with normalising flows

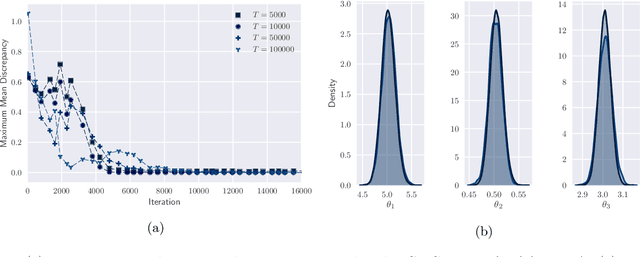
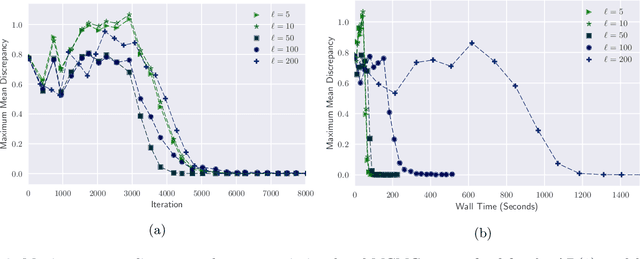
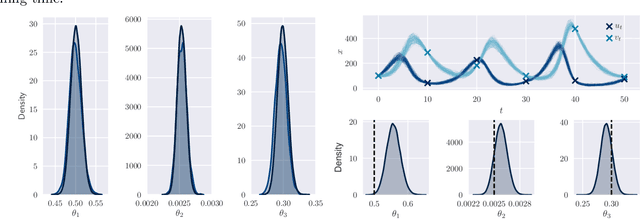
By exploiting mini-batch stochastic gradient optimisation, variational inference has had great success in scaling up approximate Bayesian inference to big data. To date, however, this strategy has only been applicable to models of independent data. Here we extend mini-batch variational methods to state space models of time series data. To do so we introduce a novel generative model as our variational approximation, a local inverse autoregressive flow. This allows a subsequence to be sampled without sampling the entire distribution. Hence we can perform training iterations using short portions of the time series at low computational cost. We illustrate our method on AR(1), Lotka-Volterra and FitzHugh-Nagumo models, achieving accurate parameter estimation in a short time.

Black-box Variational Inference for Stochastic Differential Equations

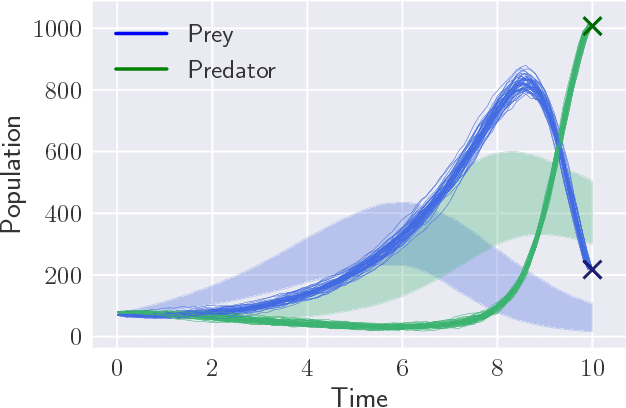
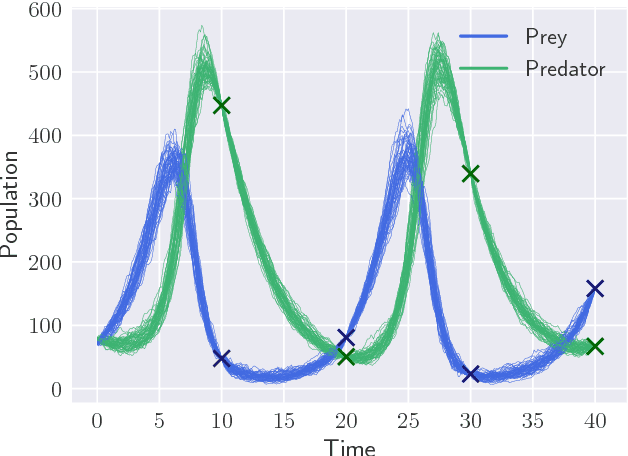
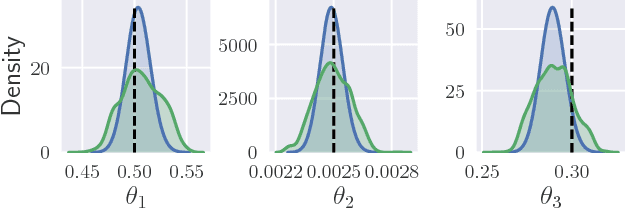
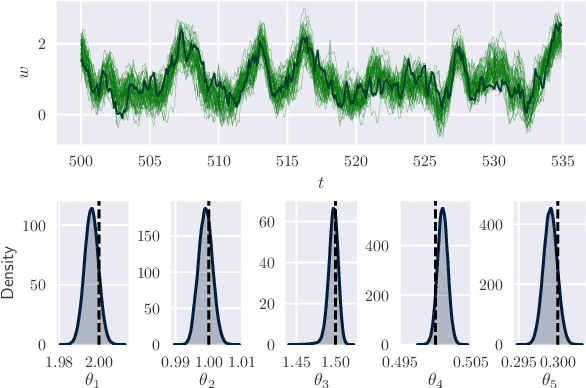
Parameter inference for stochastic differential equations is challenging due to the presence of a latent diffusion process. Working with an Euler-Maruyama discretisation for the diffusion, we use variational inference to jointly learn the parameters and the diffusion paths. We use a standard mean-field variational approximation of the parameter posterior, and introduce a recurrent neural network to approximate the posterior for the diffusion paths conditional on the parameters. This neural network learns how to provide Gaussian state transitions which bridge between observations in a very similar way to the conditioned diffusion process. The resulting black-box inference method can be applied to any SDE system with light tuning requirements. We illustrate the method on a Lotka-Volterra system and an epidemic model, producing accurate parameter estimates in a few hours.