Split Hierarchical Variational Compression

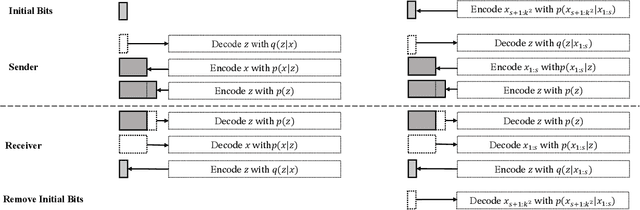
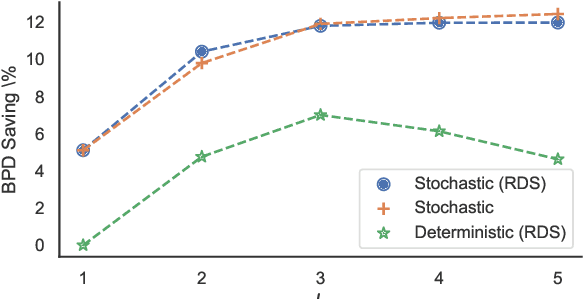
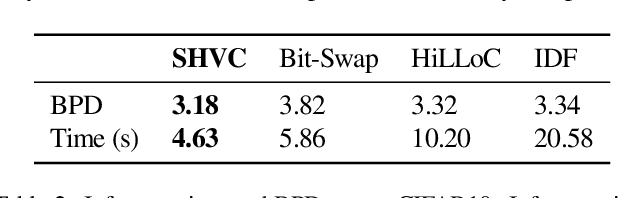
Variational autoencoders (VAEs) have witnessed great success in performing the compression of image datasets. This success, made possible by the bits-back coding framework, has produced competitive compression performance across many benchmarks. However, despite this, VAE architectures are currently limited by a combination of coding practicalities and compression ratios. That is, not only do state-of-the-art methods, such as normalizing flows, often demonstrate out-performance, but the initial bits required in coding makes single and parallel image compression challenging. To remedy this, we introduce Split Hierarchical Variational Compression (SHVC). SHVC introduces two novelties. Firstly, we propose an efficient autoregressive prior, the autoregressive sub-pixel convolution, that allows a generalisation between per-pixel autoregressions and fully factorised probability models. Secondly, we define our coding framework, the autoregressive initial bits, that flexibly supports parallel coding and avoids -- for the first time -- many of the practicalities commonly associated with bits-back coding. In our experiments, we demonstrate SHVC is able to achieve state-of-the-art compression performance across full-resolution lossless image compression tasks, with up to 100x fewer model parameters than competing VAE approaches.

iFlow: Numerically Invertible Flows for Efficient Lossless Compression via a Uniform Coder

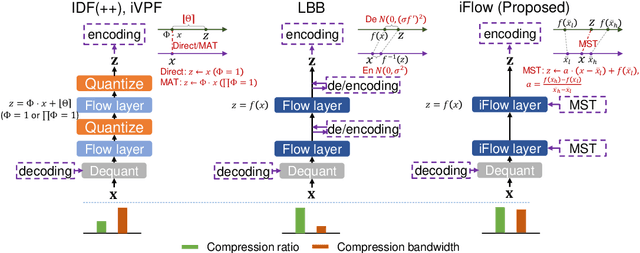
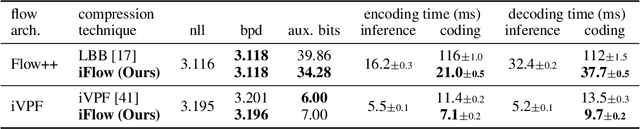
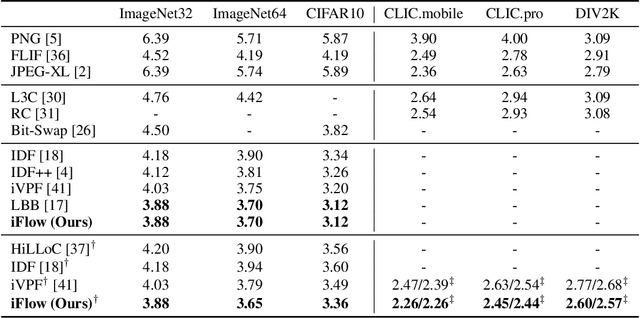
It was estimated that the world produced $59 ZB$ ($5.9 \times 10^{13} GB$) of data in 2020, resulting in the enormous costs of both data storage and transmission. Fortunately, recent advances in deep generative models have spearheaded a new class of so-called "neural compression" algorithms, which significantly outperform traditional codecs in terms of compression ratio. Unfortunately, the application of neural compression garners little commercial interest due to its limited bandwidth; therefore, developing highly efficient frameworks is of critical practical importance. In this paper, we discuss lossless compression using normalizing flows which have demonstrated a great capacity for achieving high compression ratios. As such, we introduce iFlow, a new method for achieving efficient lossless compression. We first propose Modular Scale Transform (MST) and a novel family of numerically invertible flow transformations based on MST. Then we introduce the Uniform Base Conversion System (UBCS), a fast uniform-distribution codec incorporated into iFlow, enabling efficient compression. iFlow achieves state-of-the-art compression ratios and is $5\times$ quicker than other high-performance schemes. Furthermore, the techniques presented in this paper can be used to accelerate coding time for a broad class of flow-based algorithms.

Scalable approximate inference for state space models with normalising flows

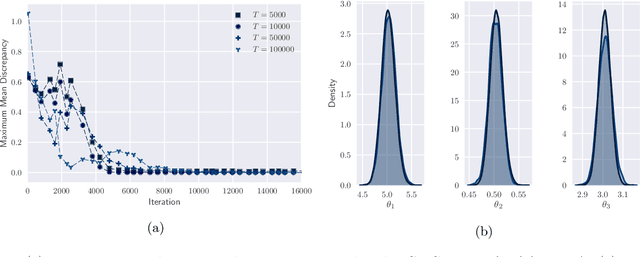
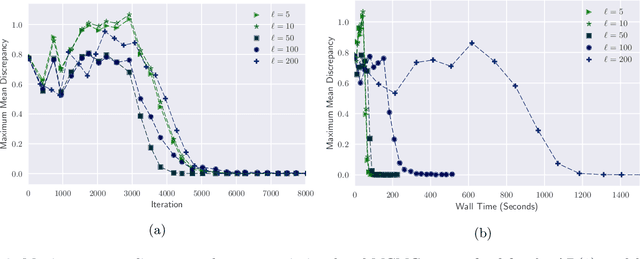
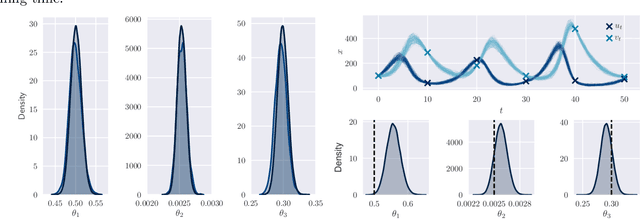
By exploiting mini-batch stochastic gradient optimisation, variational inference has had great success in scaling up approximate Bayesian inference to big data. To date, however, this strategy has only been applicable to models of independent data. Here we extend mini-batch variational methods to state space models of time series data. To do so we introduce a novel generative model as our variational approximation, a local inverse autoregressive flow. This allows a subsequence to be sampled without sampling the entire distribution. Hence we can perform training iterations using short portions of the time series at low computational cost. We illustrate our method on AR(1), Lotka-Volterra and FitzHugh-Nagumo models, achieving accurate parameter estimation in a short time.

Variational Bridge Constructs for Grey Box Modelling with Gaussian Processes

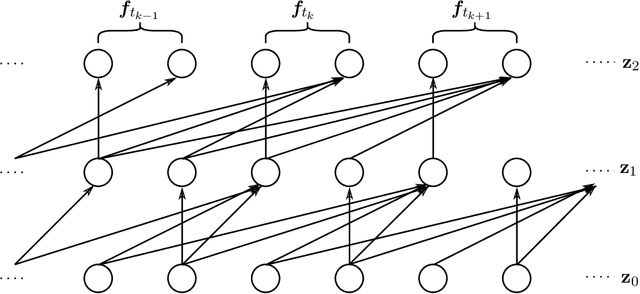
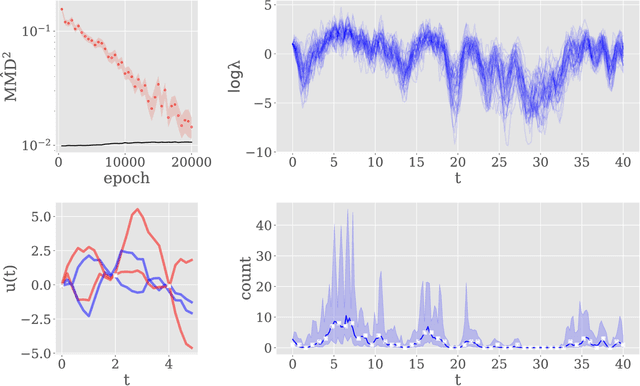
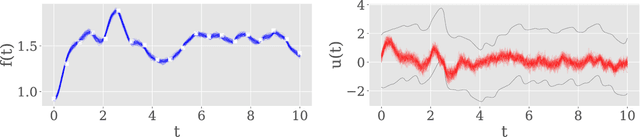
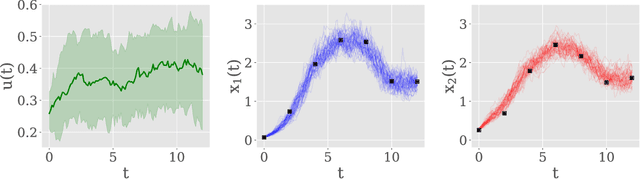
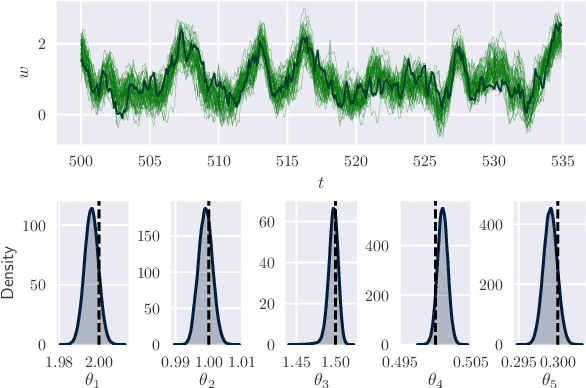
This paper introduces a method for inference of heterogeneous dynamical systems where part of the dynamics are known, in the form of an ordinary differential equation (ODEs), with some functional input that is unknown. Inference of such systems can be difficult, particularly when the dynamics are non-linear and the input is unknown. In this work, we place a Gaussian process (GP) prior over the input function which results in a stochastic It\^o process. Using an autoregressive variational approach, we simulate samples from the resulting process and conform them to the dynamics of the system, conditioned on some observation model. We apply the approach to non-linear ODEs to evaluate the method. As a simulation-based inference method, we also show how it can be extended to models with non-Gaussian likelihoods, such as count data.

Black-Box Autoregressive Density Estimation for State-Space Models

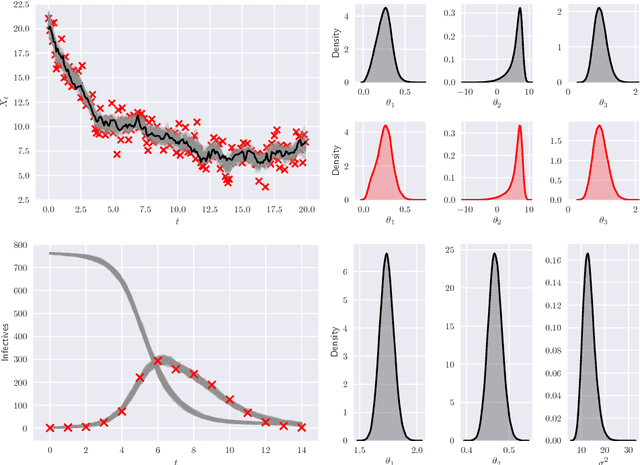
State-space models (SSMs) provide a flexible framework for modelling time-series data. Consequently, SSMs are ubiquitously applied in areas such as engineering, econometrics and epidemiology. In this paper we provide a fast approach for approximate Bayesian inference in SSMs using the tools of deep learning and variational inference.